I am a mathematics graduate student from the Philippines, and I figured out that this site is a good platform to dump my thoughts about mathematics (and possibly other geeky stuff). What I'm planning here is pretty much to regularly write about what I currently know about mathematics while trying to explain it to the general lay audience. 

So what exactly do these math people do in particular, and why do some people bother to dedicate their lives to it? You might think we've already mapped out pretty much all of mathematics right? I mean, what could we possibly need to know more about numbers? Well, for starters, mathematics spans more than the concept of numbers. Some people actually refer to mathematics as the "formal study of patterns", and while patterns are predominant in numbers, we certainly do not only see patterns in numbers.  Furthermore, we currently do **not** know everything about numbers. But just to demonstrate, let us first look at something that we do know about numbers, thus we'll define what a prime number is: it is simply any positive whole number _p_ greater than _1_  that cannot be divided by any other positive number except for itself and the number _1_. For example, _7_ is a prime number because it cannot be divided *evenly* by _2_, _3_, _4_, _5_, or _6_, and it is divisible by itself, because _7_ divided by _7_ is just _1_, and it is divisible by _1_ because _7_ divided by _1_ is just _7_. Similarly, _11_, _13_, _17_ are primes. So we have a good idea of what primes are, and we will now state an important result about them: "_for every positive number greater than 1, we can find a prime number that divides it_".  So for example, _6_ can be divided by the prime _3_ because _6/3=2_, and similarly _25_ is divisible by prime _5_ since _25/5=5_. We will use this fact, to *prove* that there are "_infinitely many primes_". To prove this, we are going to use a technique that is pretty well known among mathematicians, it's called "_proof by contradiction_", that is, we assume that something we are proving is false-- in our case, that there are only _finitely_ many primes, and we should find a contradiction if we follow along this line of reasoning. So, if we assume that there are only finitely many primes, then we should be able to list it like so: 

<center>http://quicklatex.com/cache3/95/ql_f1d2b878c0d4fc71ac41e9fa87276395_l3.png </center>
where http://quicklatex.com/cache3/74/ql_471863cafd20d577cb55131d73de8974_l3.png are all the prime numbers that you can find. Now, we make another number using these primes, let's call it _P_, and define it like so: http://quicklatex.com/cache3/5c/ql_d8af19f6bd0e6cb9b3237bda5cc10e5c_l3.png which is the product of *all* our primes plus _1_.  Now, this is the important part of the trick, we can always write _1_ as 

<center>http://quicklatex.com/cache3/cb/ql_3d3e0c78f96dfd756df22e7b65c82bcb_l3.png</center>


We use our previous result, that all positive numbers greater than _1_ can be divided by some prime, and since, we assumed that all our prime is contained in the list above, then _P_ must be divisible by one of the http://quicklatex.com/cache3/ac/ql_8156abf19e9c9c66201febcfdfa150ac_l3.png 's in the list, and without loss of generality we can just assume that _P_ is divisible by http://quicklatex.com/cache3/da/ql_69edf44c2bc0bc3f576de3f1bff651da_l3.png. Because _P_ is divisible by http://quicklatex.com/cache3/da/ql_69edf44c2bc0bc3f576de3f1bff651da_l3.png and http://quicklatex.com/cache3/44/ql_9565465a8533adfae48d85dcaedf2744_l3.png is also divisible by http://quicklatex.com/cache3/da/ql_69edf44c2bc0bc3f576de3f1bff651da_l3.png , then _1_, as the difference of two numbers which are divisible by http://quicklatex.com/cache3/da/ql_69edf44c2bc0bc3f576de3f1bff651da_l3.png , must also be divisible by the prime http://quicklatex.com/cache3/da/ql_69edf44c2bc0bc3f576de3f1bff651da_l3.png. But _1_ cannot be divisible by any prime number, because every prime number is greater than _1_, therefore we have a contradiction, hence prime numbers cannot be listed finitely. 


<br><center>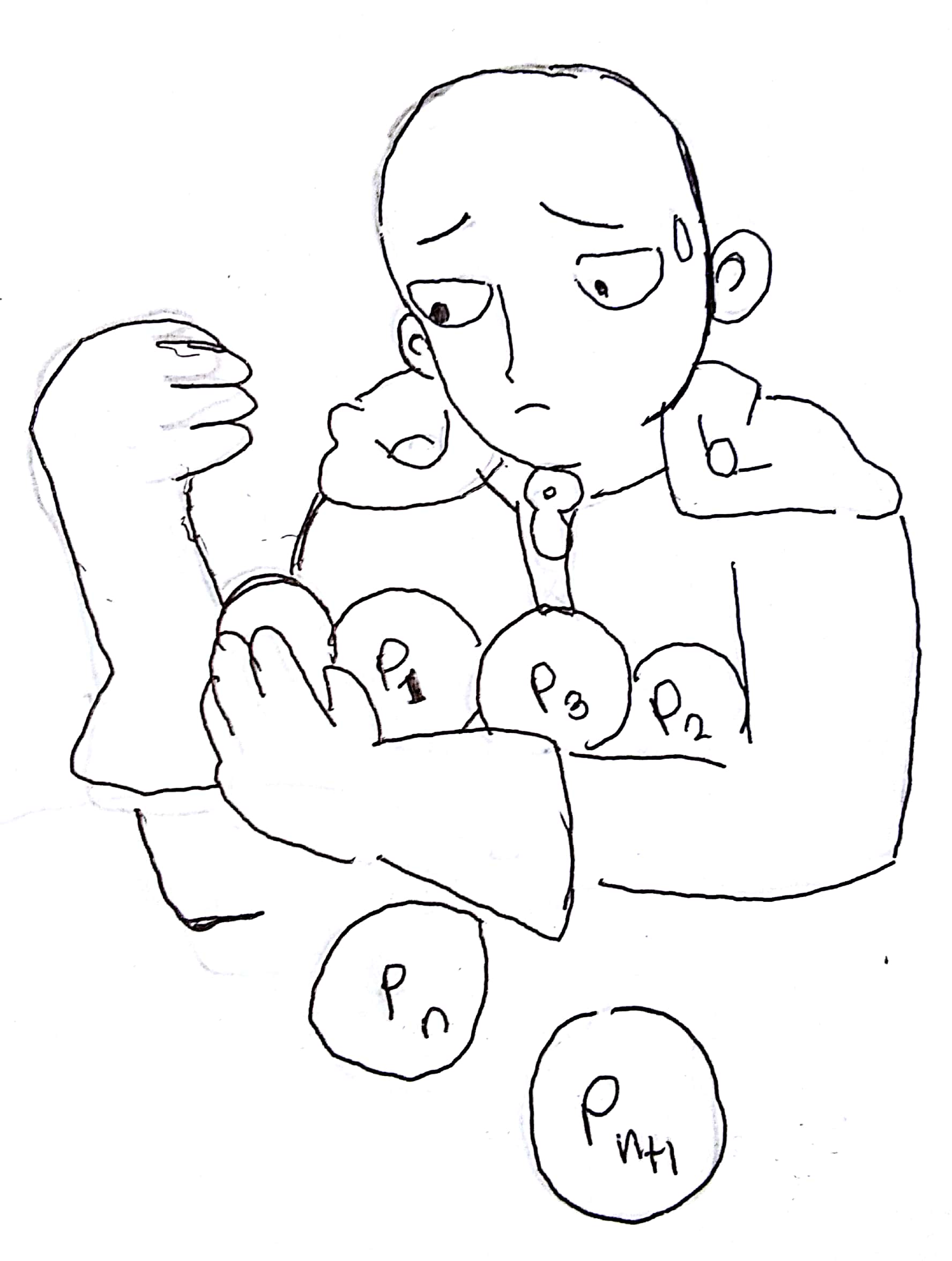![even heroes fail.jpg](https://steemitimages.com/DQmYhSEmK3KmWGVQNK1zTsBxDVtcHpsBKiJbz7QhvrG7j8v/even%20heroes%20fail.jpg)</center>
<center>*Even heroes fail*</center><br>

There you have it, that little piece of art above is what we call a _proof_, a bunch of statements stringed together by logic to arrive at a conclusion. If you made it until this point, I think you'll see that there is some exquisite beauty  in proofs, that there is something elating about understanding a mathematical proof. Also, as a matter of fact, the proof above is pretty much the same proof that [Euclid](https://en.wikipedia.org/wiki/Euclid) has shown thousands of years ago-- proofs transcend time, once found, they will always remain true for all eternity. This is what mathematicians really do, proving facts about mathematics-- not crunching *really* big numbers (some of them do that, but definitely not all), as some might think. Hence we go back to our first question, and I can say with confidence that this is the reason why some people are so hooked at math, it's just damn pretty. 

Enough of my rambling, I hope you find my first post educational, and that you'll have a newfound appreciation of maths after this.