Evaluar la continuidad de una función racional en un punto dado
hive-196387·@carlos84·
0.000 HBDEvaluar la continuidad de una función racional en un punto dado
 <center><sup>[Imagen editada de pixabay](https://pixabay.com/es/photos/pizarra-verde-la-educaci%C3%B3n-madera-2629436/)</sup></center> https://youtu.be/eQydgkAmwVU [Ver en Youtube por @carlos84](https://youtu.be/eQydgkAmwVU) --- <div class="text-justify"> Saludos amigos de hive. Antes de evaluar la continuidad de la función racional explicada en el presente recurso audiovisual, me gustaría que pr visualizarán la siguiente imagen que fue elaborada utilizando el software geogebra 5.0 y las herramientas de diseño de Microsoft Power Point: 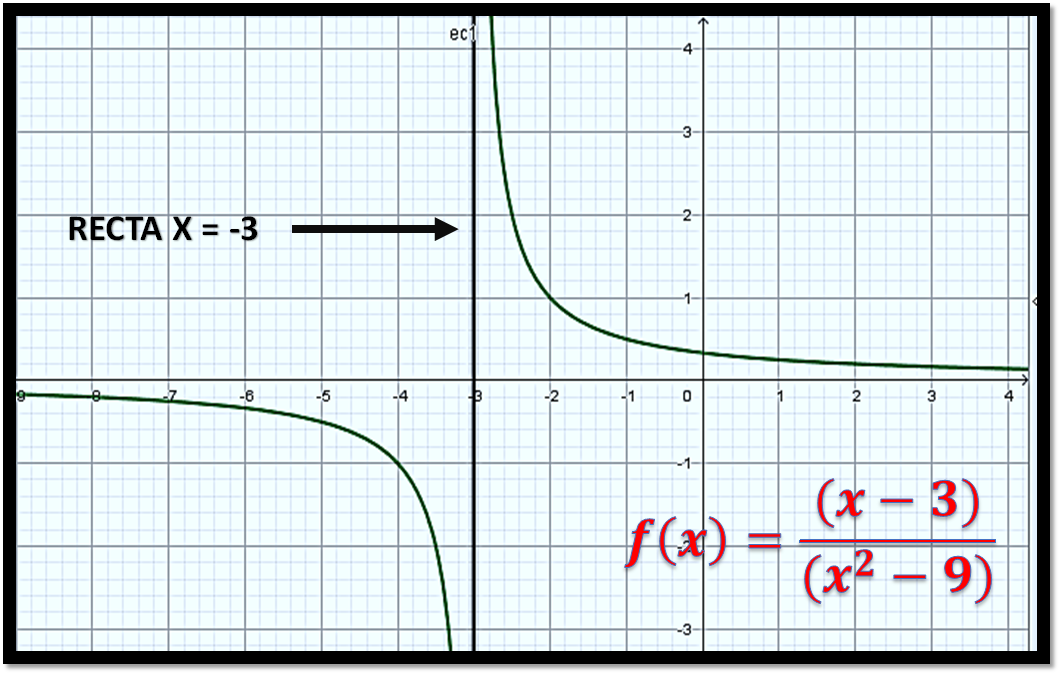 <center><sup>Autor de la imagen: @carlos84</sup></center> En la imagen anterior se puede ver como la imagen presenta una discontinuidad del tipo evitable para el punto x= 3 que también termina siendo el punto de discontinuidad de la función y que se puede corroborar mediante la teoría del límite de una función real. Si se realiza el límite de cuando x tiende al 3 nos damos cuenta que la función presenta una forma indeterminada 0/0 pero que factorizando para este caso el denominador nos damos cuenta que podemos cancelar términos y encontrar un valor del límite, lo que nos hace concluir que la función es discontinua evitable para x=3. Lo otro importante es que para el punto x=-3 el límite de cuando x tiende a -3 nos da infinito, razón por la cual para x=-3 es una recta vertical paralela al eje Y que sirve como asíntota de la función tal y como lo pueden ver en la imagen anterior. Para ver otros detalles adicionales que sirven para evaluar la continuidad de la función racional, les invito a visualizar el recurso audiovisual en mención. --- [Ver en Youtube](https://youtu.be/eQydgkAmwVU) </div>
👍 tonimontana, stemd, tonimontana.neo, toni.ccc, toni.pal, malenavargas, elkaos, limka, laissez-faire, jk6276, vxc.tra, vxc.stem, aqua.nano, ew-and-patterns, katysavage, carlos84, mafia.wallet, suonghuynh, onthewayout, forensic911, quochuy, steemulant, pocketjs, hf19, mtzrene, juanmolina, zuerich, ramonycajal, roadstories, cervantes, mariu.espinoza, gardenofcarmen, kpopjera, kirito-freud, kantos, jvphotography, pabloptimista, javyeslava.photo, roadstories.trib, gargon, pgarcgo, jgcastrillo19, mendezand, dechastre, goldrooster, tiababi, roinv, reinaseq, pvinny69, aleestra, palasatenea, miguelbaez, neilamarcano, hashzone91, loudutim, jesus68, peterpanpan, dulcinea, tsoldovieri, gabox, artemisjane26, simonmaz, meno, cataluz, garvi, chopiliart, joso, aliriera, melor9, patris, renataboreal, meppij, marievar, wartrapa, titin, cuvi, christianytony, gunthertopp, fnux, fdataline77, maastro, battebilly, hijosdelhombre, hadley4, pialejoana, perniachiquito, lizdeluca, javier.dejuan, bit4bit, arnaldoropeza, iamsaray, maruskina, rosana6, axel-blaze, im-ridd, rz1996, mayfhelg, teo, azmielbanjary, votepower, velazquezboy, titan-c, gregorior, oliviagm, albagargon, mdcomes, noticias, cervantes.one, reimerlin, jkj, neymarjr, spanishchef, aneblueberry, ibiza, magoia, heiditravels, teacher, luisucv34, kilianmiguel, fidel-castro, mpandrew, soymanu, kranga, freecreative, mariacherries, dinocreative, daribel, blocktrades, tomatom, kgakakillerg, investegg, trans-juanmi, lizanomadsoul, manncpt, jnmarteau, globalschool, gabrielatravels, daniel.dalo, yehey, afrikablr, esthersanchez, council, juanfb, coquiunlimited, julian.alejandro, dinaudic, mike961, david.dicotomia, mammasitta, massivevibration, onartbali, danieli98, rafarosado, irvinc, fulani, yiobri, cyprianj, creary, chaodietas, trangbaby, gentleshaid, hadji, stemng, samest, kingabesh, the.chiomz, djoi, menoski, temitayo-pelumi, loveforlove, empressteemah, payroll, hannymarchan, lemouth, steemstem-trig, omstavan, lesmouths-travel, minnowbooster, howo, aboutcoolscience, robotics101, itastem, steempsych, scienze, scienza, the-rhapsodist, steemstem, dna-replication, justtryme90, lamouthe, techslut, valth, dhimmel, bloom, mobbs, helo, samminator, mahdiyari, alexander.alexis, ludmila.kyriakou, abigail-dantes, felixrodriguez, noloafing, gotgame, gra, postpromoter, sankysanket18, kenadis, sco, intrepidphotos, fragmentarion, terrylovejoy, dexterdev, geopolis, alexdory, flugschwein, charitybot, francostem, de-stem, deholt, motherofalegend, marcuz, urdreamscometrue, pboulet, meanroosterfarm, stem.witness, crowdwitness, walterprofe, nazer, kaeves4711, joshmania, mengene, stemsocial, hive-101493, roelandp, croctopus, marcus0alameda, doctor-cog-diss, jtm.support, liambu, bilpcoinbpc, shinyrygaming, enzor, curie, uwelang, iamjadeline, vietthuy, epicdice, thesoundof, lastminuteman, redrica, mulletwang, holbein81, videosteemit, thexbttrader, disagio.gang, alaqrab, reddust, val.halla, thelordsharvest, yangyanje, cryptononymous, itchyfeetdonica, bellaian, silentscreamer, braaiboy, julialee66, indigoocean, gwilberiol, minerthreat, myfreebtc, bflanagin, steemstorage, rem-steem, cryptofiloz, fsm-core, modernzorker, federacion45, investingpennies, betterthanhome, jlsplatts, mejustandrew, utube, fantasycrypto, koenau, brianoflondon, kevinwong, damla, sportscontest, didic, citimillz, doikao, blewitt, khasa, alexxxdada, shimozurdo, risingstar2, chris4210, tfeldman, revo, trevorpetrie, stahlberg, tobias-g, vonaurolacu, qberry, rambutan.art, jancharlest, trisolaran, hairgistix, fi2eedom, deeanndmathews, theisacoin, redpalestino, cacalillos, locikll, kimzwarch, steveconnor, d-vine, carn, photohunt, takowi, idkpdx, superlotto, bscrypto, greddyforce, incubot, barbz, cakemonster, urtrailer, askari.ccc, simba, anwenbaumeister, yadamaniart, apsu, sustainablyyours, stayoutoftherz, revisesociology, braveboat, toocurious, lays, johnspalding, miroslavrc, scottcbusiness, vittoriozuccala, lorenzopistolesi, andrewharland, schroders, questcrypto, tombstone, kpine, hendrikdegrote, briggsy, minnowpowerup, dauerossi, beverages, stk-g, zipporah, dailyspam, mindblast, kylealex, spoke, marcocasario, double-negative, sallhiddles, edencourage, yourtop3, quello, the100, thecryptodrive, matt-a, tristancarax, sokha, neumannsalva, torico, yangoldberg, drmake, mhm-philippines, irgendwo, technologycorner, musicvoter2, goblinknackers, the.success.club, waltermeth, almightymelon, thepeakstudio, scalextrix, bradfordtennyson, plantstoplanks, upme, lightflares, vicesrus, nateaguila, solarphasing, fractalfrank, gloriaolar, hornetsnest, forester-joe, notconvinced, majes.tytyty, helgalubevi, ambyr00, djennyfloro, neneandy, movingman, arcange, fengchao, roamingsparrow, wolven-znz, yuurinbee-znz, serylt, perpetuum-lynx, driptorchpress, hhayweaver, norwegianbikeman, rihc94, raphaelle, scholaris, steemitboard, sc-steemit, smalltall, meanbees, edgarsart, leoumesh, verhp11, violetmed, mcsvi, firstamendment, drlobes, unicron, ibt-survival, charlie777pt, forykw, sostrin, diverse, travoved, chungsu1, sanderjansenart, celinavisaez, morarnagringa, reggaesteem, wanderingmoon, hive.consultant, pladozero, usualsidekick, mister.reatard, lightcaptured, stem-espanol, elvigia, lorenzor, iamphysical, azulear, carloserp-2000, vjap55, miguelangel2801, emiliomoron, delpilar, josedelacruz, andrick, yusvelasquez, acont, fran.frey, giulyfarci52, wilmer14molina, capp, tomastonyperez, calatorulmiop, uche-nna, dubignyp, thelogicaldude, fatkat, herzinfuck, amestyj, robmojo, iptrucs, ubaldonet, binkyprod, supriya1993, buttcoins, danile666, cmmemes, sargewhale, rodrigocassio, silviomangum29, viagens, mariusfebruary, embot, sandymeyer, dna.org, juanbg, nockzonk, medro-martin, realblockchain, wesphilbin, acousticguitar, sciencevienna, gribouille, bennettitalia, vaultec, eric-boucher, stevenwood, stevejhuggett, robertbira, eliaschess333, farizal, eniolw, yourfuture, amansharma555, bitcome, lk666, flatman, oghie, orlandogonzalez, gifty-e, ennyta, gaming.yer, endopediatria, anaestrada12, abbenay, sonofsatoshi, andre-verbrick, zorg67, abneagro, proconocimiento, alexandermoreno, carlosbp,