2-1 Fermi-Dirac 확률분포와 Sigmoid 함수와의 관계
kr·@codingart·
0.000 HBD2-1 Fermi-Dirac 확률분포와 Sigmoid 함수와의 관계
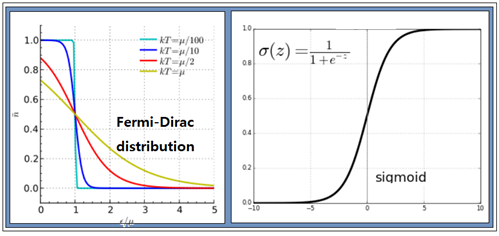 Fermi-Dirac 입자들의 확률 분포를 구해보자. 동일한(identical) ni개의 입자들이 에너지 레벨을 Ei 로 가정하자. 에너지 레벨 Ei 는 다시 구별이 가능한 서브레벨 gi (degeneracy)를 가지며 각 서브 레벨은 최대 1개의 입자를 포함하거나 비어 있을 수 있다. 에너지 레벨 Ei 는 크기만을 지정하는 스칼라 양이므로 설사 에너지 레벨이 같다고 해도 입자들의 운동량은 벡터이므로 운동 방향이나 회전 방향이 서로 다를 수 있으므로 이들이 속해 있는 서브레벨은 서로 구별이 가능하다. 에너지 레벨이 Ei 에 해당하는 gi 개의 서브레벨에 ni 개의 입자들이 각 서브레벨 별로 최대 1개의 입자를 포함하거나 비어 있게 될 경우의 수를 계산해 보자. 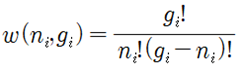 에너지 레벨 Ei 를 사용하여 전체 에너지 레벨의 경우의 수를 계산해 보자. 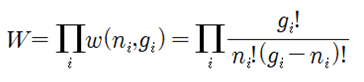 Boltzman 확률분포 유도과정을 따라 W가 최대값을 가지게 되는 즉 가장 probale 한 물리적 상태를 찾아보자. 통계약학의 Microcanonical Ensemble 에 해당하는입자분포 ni 는 2개의 구속조건(Constraints)을 만족시켜야 한다. 즉 전체 입자의 수는 N 이며 전체 에너지 값이 일정한 값 E 라는 조건을 만족해야 한다. 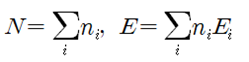! 한편 볼츠만의 엔트로피는 경우의 수 W에 대한 자연로그를 취하고 볼츠만 비례상수 kB 를 곱한 형태로 주어진다. 전체 입자수 및 전체 에너지가 일정하다는 조건들을 라그랑즈 승수 기법을 적용하여 다음과 같이 하나의 식으로 표현하고 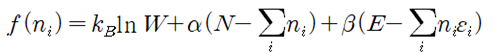 볼츠만의 엔트로피를 최대화 할 수 있도록 즉 ni 에 대해서 편미분하여 그 결과를 0 으로 두자. 이 과정에서 큰 수의 Factorial 값들에 대해서 Stirling 의 근사공식 적용이 이루어지며 다음과 같은 형태의 입자 분포 식이 얻어진다. 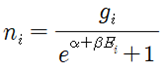 각 서브레벨별 평균 입자 수는 다음과 같이 표현된다. 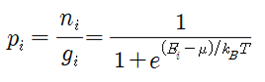 T는 절대온도 K 이다. μ는 화학적 포텐셜(Chemical Potential) 또는 Fermi level 이라고도 한다. 만약 특정 소재 속의 입자의 에너지 레벨이 Fermi level 값에 해당하는 μ 라면 pi 값이 (1/2)임을 알 수 있다. 한편 에너지 레벨의 값이 Fermi level 값 μ 보다 훨씬 크다면 pi 값이 1.0에 가까워지며 반면에 에너지 레벨의 값이 Fermi level 값 μ 보다 훨씬 작다면 pi 값은 0.0에 가까워진다. 즉 pi 는 확률밀도 함수가 아니라 likelyhood 함수에 해당하며 머신러닝에서는 랜덤하게 계산되는 hypothesis 값에 대하여 카테고리를 부여하기 위하여 다음과 같이 Sigmoid activation 함수로 표현할 수 있다. Hi 는 랜덤 넘버를 사용하여 계산되기 때문에 입자의 에너지처럼 항상 양의 값이 아니며 ∓값을 가질 수 있다. 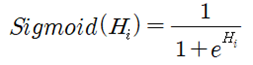 뉴론에서 출력하는 값인 hypothesis 가 0.5 이상이면 즉 카테고리가 “True” 이거나 “1” 이며 0.5 이하이면 카테고리가 “False” 이거나 “0” 이 되므로 이원 분류(Binary Classification)에 사용이 가능하다. ![마나마인로고.png] https://cdn.steemitimages.com/DQmeePhYx37SUt2zaQJZjJZenWLWSyeK2zKiEp2erB77Lhb/%EB%A7%88%EB%82%98%EB%A7%88%EC%9D%B8%EB%A1%9C%EA%B3%A0.png
👍 codingart, ravenkim, yehey, pinoy, eii, fortune-master, passion-fruit, beoped, anpigon, talken, steemory, pigoncchio, wony, bramd, mmmagazine, ronbong,