![noname12.png](https://cdn.steemitimages.com/DQmPasCZuEH7tM3S7D38k22u7wwU3JZ7mj6tuxAvYU58HQY/noname12.png)


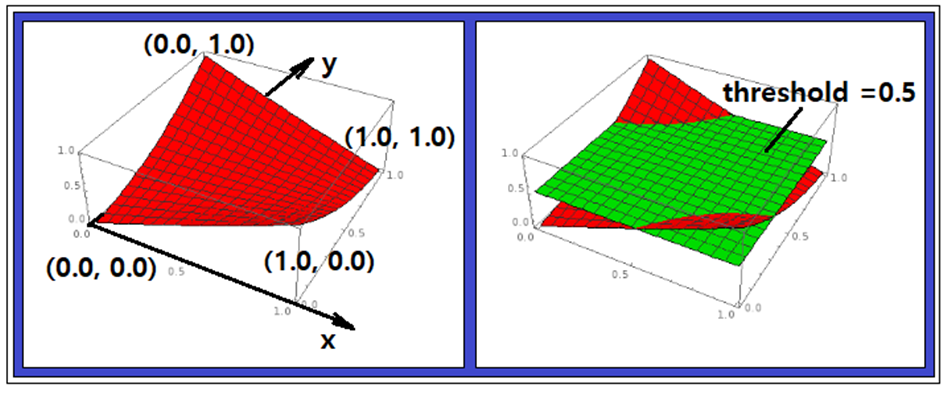그렇다면 최종적으로 결정된 hypothesis 함수가 어떤 의미인지 매스매티카 3차원 그래픽에 의해 알아보기로 하자.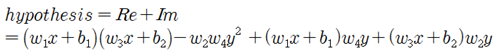

![noname11.png](https://cdn.steemitimages.com/DQmc4Jisvdj9Dg8ApoZzUyUFbhvUdt36is27WdEXmnVkfiT/noname11.png)

이 글은https://steemit.com/kr/@codingart/3-8-pole-xor-hypothesis-i 에 이어지는 글입니다.

x, y를 2개의 독립변수로 하는위 그림의  이 3차원 곡면 함수를 매스매티카로 코딩하여 출력한 결과를 살펴보자. (0.0, 1.0) 과 (1.0, 0.0) 이 “1” (0.0, 0.0) 과 (1.0, 1.0) 이 “0”으로 분류되었다.

XOR 논리 머신 러닝에서 hypothesis에서 0.0이 아닌 임의의 α값에 대해 XOR 출력 값을 계산할 수 있으나 α값 변화에 따라 폴 값이 바뀌게 된다. 하지만 임의의 α값을 사용하는 hypothesis 들 간의 공통점은 다음의 9개항들이 포함된다는 점이다.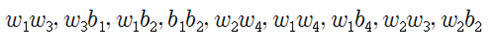

![noname13.png](https://cdn.steemitimages.com/DQmWqg6xSt6fwJwXrwTUbiuFkrogw6Y8PVK2nbfqzYeb2rZ/noname13.png)

한편 현재의 복소수 기법을 사용하여 구성한 hypothesis를 사용하여 XOR 논리 문제를 처리할 수 있지만 hypothesis 구성 방법에는 다양한 가능성이 있을 수 있으므로 앞에서 지적했던 9개항을 포함하도록 하는 hypothesis를 직관적으로 구성해서 코드를 실행해 보자.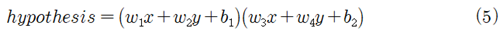 

![noname18.png](https://cdn.steemitimages.com/DQmdLwvm3UBLTdb3V93LrLdvUdBhe88yh3iWSTS71QZ1zbf/noname18.png)

![noname14.png](https://cdn.steemitimages.com/DQmVfs9giToNUUon8iAM3xMdYbHfPx4peqdStiozTFrWWm7/noname14.png)
x, y를 2개의 독립변수로 하는 이 3차원 곡면 함수를 매스매티카로 코딩하여 출력한 결과를 살펴보자. 앞서의 결과와 비교해 보면 위쪽으로 볼록하다는 점이 다르다. 하지만 threshold = 0.5 인 면을 기준으로 (0.0, 1.0) 과 (1.0, 0.0) 이 “1” (0.0, 0.0) 과 (1.0, 1.0) 이 “0”으로 분류되었다.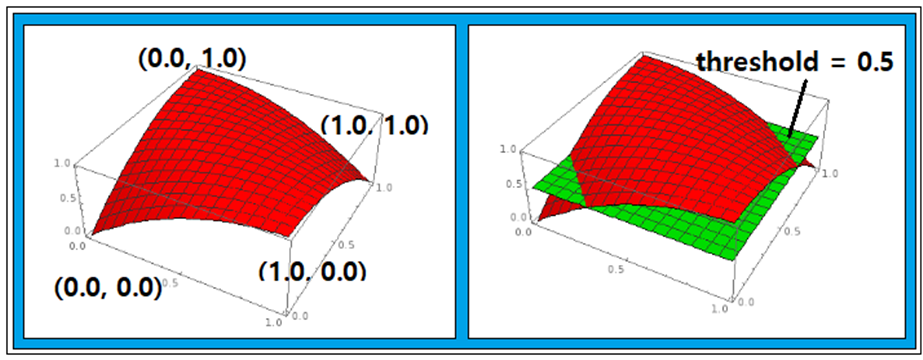

![noname15.png](https://cdn.steemitimages.com/DQmPAfju3XnSk6mp5qjEZq9AQJuWS61GLzqBE84pdVNxLLd/noname15.png)

복소수 기법과 동일한 잘 수렴하는 hypothesis  값들이 계산된다. 복소수 기법과 직관적 기법과의 차이를 지적한다면 의 부호가 바뀐다는 점이지만 hypothesis 학습 결과는 동일하다는 점에서 등가로 볼 수 있다.

직관적으로 설정된 (5)식의 hypothesis를 사용한 예제 코딩은 필자의 2018년 졸저 “파이선 코딩 초보자를 위한 텐서플로우와 OpenCV 머신 러닝” 3장 13편에서 다루었으니 참조하기 바란다.

![noname19.png](https://cdn.steemitimages.com/DQmPPkFxznhWF7xL63z9GfZ3ZBB9psgjjyo9sT1dobUB4eW/noname19.png)

한편 XOR 논리 문제를 풀기 위한 위의 conventional 뉴럴 네트워크 알고리듬에 따른 hypothesis는 레이어 별로 firing을 위한 Sigmoid 함수 처리를 포함하여 웨이트 매트릭스의 엑스포넨셜 함수 형태가 된다.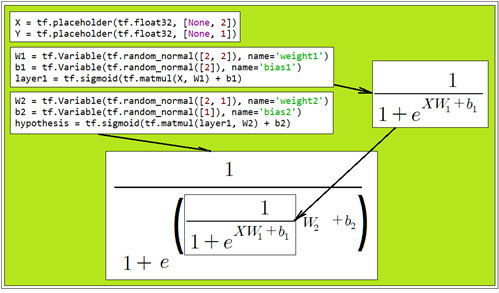 

![noname17.png](https://cdn.steemitimages.com/DQmc2HAyGxbQ45mExdD52gead52Lhmi2tXXQe4DQtHjrCLQ/noname17.png)

아울러 각 레이어 단계별로 입력벡터 웨이팅 후 선형적으로 Σ 합산 처리가 이루어지지만 복소수로부터 유도되는 hypothesis 의 경우에서는 지금까지의 뉴럴 네트워크 모델링 기법과는 달리 Π 곱하기 처리됨에 유의하자.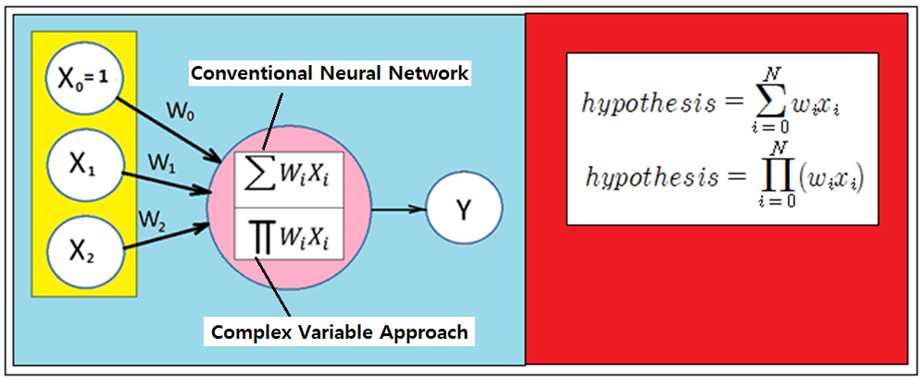 

![noname01.png](https://cdn.steemitimages.com/DQmNgHJXQwWPgUCjfmN9Cq6Lr7fYVzX4SVFUfH89YDBr7iP/noname01.png)

이 2가지 방법은 선형 hypothesis를 다루는 경우에는  아무런 차이가 없지만 비선형 영역을 다루기 위해서는 현격한 차이가 있음을 인식하자.

![마나마인로고.png](https://cdn.steemitimages.com/DQmeePhYx37SUt2zaQJZjJZenWLWSyeK2zKiEp2erB77Lhb/%EB%A7%88%EB%82%98%EB%A7%88%EC%9D%B8%EB%A1%9C%EA%B3%A0.png)