5-11 Information Bit number 및 Entropy 계산
kr·@codingart·
0.000 HBD5-11 Information Bit number 및 Entropy 계산
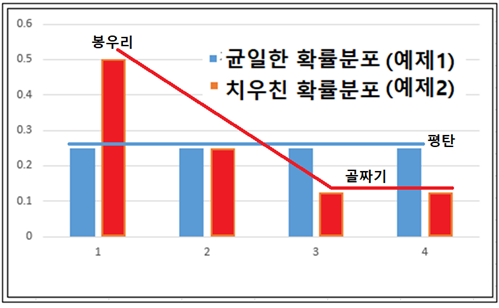 Wikipedia나 Sebastian Raschka의 “Python Machine Learning“ 책에서 Information Gain과 엔트로피에 관해 읽어 보면 알 수 없는 내용으로 가득 차 있다는 점을 쉽게 알 수 있다. 저자들이 내용을 모른다고는 할 수 없으나 일반인들이 이해할 수 있는 언어로 해설되어 있지 않다는 점은 분명하다. 세상에 수많은 전문가들이 있어 연구 후 자신의 업적을 논문이나 저서를 출판함에 있어서 문제는 남들이 이해하든 못하든 상관없이 자신이 이해한 수준으로 출판한다는 점이다. 하지만 지금은 오픈소스의 시대이기 때문에 단순한 오픈을 넘어서 비밀스런 내용의 결과까지도 대중이 이해할 수 있는 수준으로 정확하면서도 알기 쉬운 해설이 필요함은 당연하다 할 것이다. 1948년 MIT에서 정보과학의 기초를 닦았던 Claude Shannon 교수의 통신에 대한 기본이론과 예제로부터 시작해 보자. Shannon 이 볼츠만 엔트로피로부터 정립한 비트 수 계산법에 관해서 알아보기로 하자. 현대의 이동 통신에서 엔코딩 방식에 따른 평균 비트수 값의 차이는 결국 데이터 통신 비용 산정에 직결되는 내용이 될 것이다. 랜덤 변수 X 의 가능한 값들이 A, B, C, D 라고 할 때에 다음의 “BAACACCDD CDADABCDBBB…” 문자열 메시지를 철자별 출현 빈도수의 확률로 분석해 보자.  예제1 이 문자열 데이터를 ‘0’과 ‘1’을 사용하면서 엔코딩하려면 각 문자별로 다음과 같이 각 2비트를 사용하여 엔코딩 할 수 있을 것이다. “0100001001001110110011111100…”  하지만 영문 문장의 문자열에 모든 철자들이 동일한 빈도수 내지는 확률로 나타나지는 않으므로 다음과 같은 경우를 고려해 보기로 하자. 문자열이 길어질 경우를 감안해서 평균 비트수를 1.75 로 엔코딩 할 수 있는지 알아보자.  아래 표에서 Code 의 비트 수를 합하면 9가되고 Value 수가 4 이므로 평균 비트 수는 비트 수와 확률을 곱하여 합산하면 1.75가 된다. 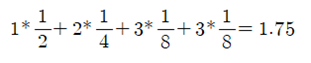 만약 3개의 철자 A, B, C 가 동일한 빈도수 확률로 나타나는 경우를 고려해보자. 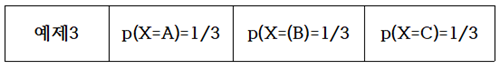 아래와 같이 엔코딩 한다면 평균 비트 수는 2가 될 것이다.  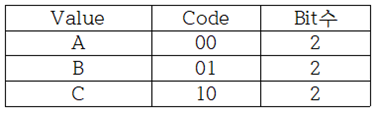 이 문제에 있어서 엔코딩 방법을 달리하여 평균 1.6비트로 엔코딩할 수는 없을까? 1.67비트가 가능하다. 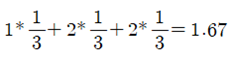 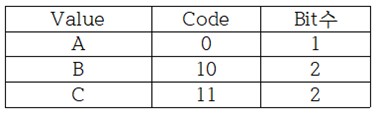 예제 2번으로 돌아가자. 문자열에서 철자 A 가 50% 출현하므로 A의 비트 수를 1.0으로 두면 25% 출현하는 철자 B 는 B의 비트 수가 1.0 보다 적어져야 할 것인지 커져야 할 것인지 다음 계산을 통해 알아보자. 각 비트 수를 –log2(p) 함수를 사용하여 계산해 보자. 2는 log 함수의 base를 뜻하는 것으로 한다. 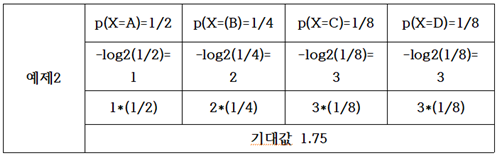 평균 비트수는 엔트로피 공식과 유사하게 다음 공식을 사용하여 계산할 수 있다. 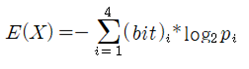 이 수학적인 형태는 볼츠만 확률 분포로부터 유도되는 아래의 엔트로피 공식과 비교해 볼 경우 log 함수의 base 값이 다르지만 둘다 모드 최소화의 대상이라는 점까지 매우 비슷해 보인다. 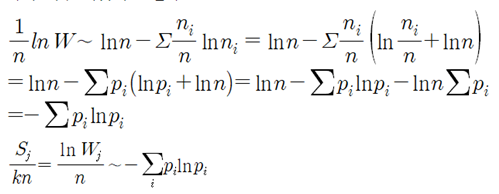 이러한 비트 수 계산법은 1950년대 미국 MIT 공과대학 교수로서 정보과학분야에 큰 업적을 남긴 Shannon 에 기인한다. 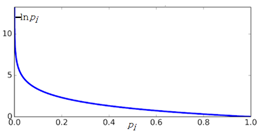 볼츠만 분포에서 에너지 레벨 별 microstate 수에 따른 확률 계산법에 의하면 입자들이 에너지 레벨 값이 가장 작은 값이나 최대 값에 쏠리게 되면 엔트로피 값이 거의 0.0에 가까워진다. 이 점은 확률 pi 가 0에 가까울수록 lnpi의 값은 무한대로 커지지만 L’Hospital 정리에 의하여 -pilnpi⤍0이 극한 값을 가지며 반대로 확률 pi 가 1에 가까워져도 0에 근접하게 된다는 사실이다. 즉 비트 수 계산에 있어서도 log 함수의 BASE 값만 다를 뿐 함수 형태가 동일하므로 예제2에서 처럼 철자 A가 출현할 빈도수 확률이 가장 높은 경우 일종의 봉우리와 골짜기 형태가 나타날 가능성이 높아져 확률적으로 식별해 내기가 용이하므로 예측하기가 쉬워진다. MNIST 머신 러닝에서 argmax 함수를 사용하는 방법의 근거이기도 하다. 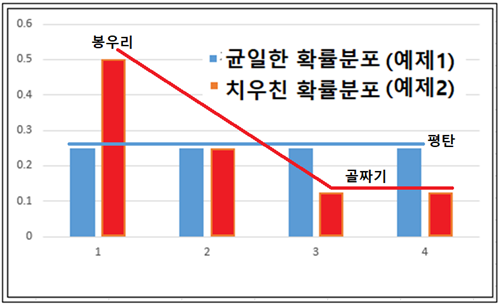 반면에 입자들의 에너지 레벨 별 분포가 일정해지면 위 수치 예제에서 보듯이 예제1의 경우처럼 각 경우별로 비슷한 확률 분포를 가지며 비트 수 내지는 엔트로피 값이 최대값이 된다. 이산적인 확률 값을 계산한 볼츠만의 기체 입자 모델에서는 용기 속에서 입자들의 에너지 레벨 값이 즉 최소값과 최대값에 치우친 경우 해당하는 엔트로피 값이 작아지는 반면에 입자들이 여러 에너지 레벨에 골고루 분산되어 있는 경우에 엔트로피 값이 커짐을 알 수 있다. 따라서 Shannon 의 비트 수와 볼츠만 엔트로피가 동일한 것은 아니지만 계산 결과를 놓고 보면 방법상 상당히 유사성이 있음을 알 수 있다. 