6-14 Sin(1.0/x) 함수의 RNN LSTM에 의한 학습과 예측
kr·@codingart·
0.000 HBD6-14 Sin(1.0/x) 함수의 RNN LSTM에 의한 학습과 예측
미적분학의 Taylor Maclaulin 급수 전개 이론에 의하면 한 점의 함수 값이 알려 지고 함수가 미분 가능하면 그 점에서 가까운 지점에서의 값을 급수 전개식에 의해 계산이 가능하다.
반면에 RNN 머신 러닝에 의해서는 함수의 시작부분 구간의 토막 정보를 초기 조건으로 이용하여 토막 구간 범위를 넘어서는 보다 넓은 범위까지 예측 계산이 가능하다. 이는 복소수 이론에서 다루는 해석적 연속(Analytic Continuation) 기법과 유사하다고 볼 수 있다.
구간 전체에서 10% 토막 구간의 Sin(x) 함수 정보를 사용하여 RNN 알고리듬에 의한 나머지 부분 예측 계산애서 주기는 정확하게 예측 계산했으나 진폭 측면에서는 다소의 오차가 발생했다.
반면에 이번에는 주기함수인 Sin 함수를 사용하되 비주기적인 거동을 보일 수 있도록 Sin(1.0/x) 라는 특별한 함수를 사용하여 학습과 테스트를 해 보기로 한다. 이 함수는 Calculus 책애서 연속성 문제를 분석하기 위해서 자주 사용되는 예제인데 함수의 그래프 자체가 아래위로 진동하되 주기가 점차 늘어나는 변동적인 특성을 보여 준다.
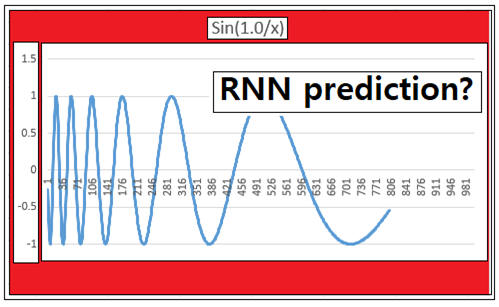
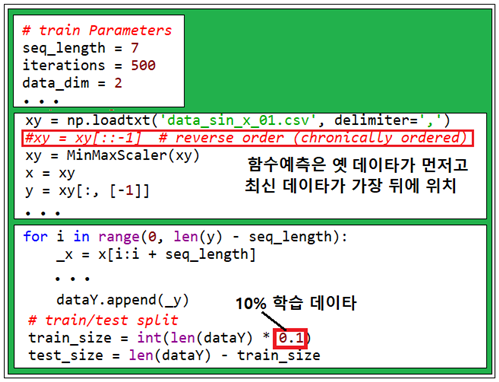
이 문제를 RNN 코드로 다름에 있어 csv 엑셀 데이터만 준비하면 된다. 엑셀 데이터 준비 과정은 이전 블로그를 참조하기 바란다.
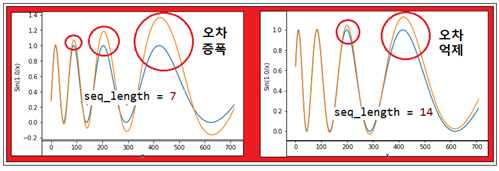
sequence_data 값을 파라메타로 하여 7인 경우와 14인 경우를 계산하였다. 이 값을 무작정 늘린다고 정밀도가 증가하지는 않는다. 하지만 적절한 값 선택에 의해서 초기 학습구간에서 멀어짐에 따라 나타날 수 있는 오차의 증폭 즉 발산 억제가 가능해 보인다.
RNN 알고리듬이 상당히 복잡하기 때문에 명쾌하게 설명하기는 어렵지만 우리가 알고 있는 미적분학에서의 급수전개 이론이나 복소수 이론에서의 해석적 연속기법에 버금갈만한 쿨한 머신 러닝 기법으로 보인다. 미적분학 방면으로 많은 응용이 기대된다.
이 예제를 돌려 보기 위한 엑셀 데이터 파일은 각자 준비하기 바라며 파이선 실행코드를 같은 폴더에 두도록 한다. 아울러 파이선 코드 다운 로드 시에 Session 부분의 indentation 훼손 여부를 반드시 확인해 보기 바란다.
#rnn_sin1_x_predictionj.py
import tensorflow as tf
import numpy as np
import matplotlib
import os
tf.reset_default_graph()
tf.set_random_seed(777) # reproducibility
if "DISPLAY" not in os.environ:
#remove Travis CI Error
matplotlib.use('Agg')
import matplotlib.pyplot as plt
def MinMaxScaler(data):
''' Min Max Normalization
Parameters
----------
data : numpy.ndarray
input data to be normalized
shape: [Batch size, dimension]
Returns
----------
data : numpy.ndarry
normalized data
shape: [Batch size, dimension]
References
----------
.. [1] http://sebastianraschka.com/Articles/2014_about_feature_scaling.html
'''
numerator = data - np.min(data, 0)
denominator = np.max(data, 0) - np.min(data, 0)
#noise term prevents the zero division
return numerator / (denominator + 1e-7)
#train Parameters
seq_length = 7
iterations = 500
data_dim = 2
hidden_dim = 10
output_dim = 1
learning_rate = 0.01
#Open, High, Low, Volume, Close
xy = np.loadtxt('data_sin_x_01.csv', delimiter=',')
#xy = xy[::-1] # reverse order (chronically ordered)
xy = MinMaxScaler(xy)
x = xy
y = xy[:, [-1]] # Close as label
build a dataset
dataX = []
dataY = []
for i in range(0, len(y) - seq_length):
_x = x[i:i + seq_length]
_y = y[i + seq_length] # Next close price
print(_x, "->", _y)
dataX.append(_x)
dataY.append(_y)
#train/test split
train_size = int(len(dataY) * 0.1)
test_size = len(dataY) - train_size
trainX, testX = np.array(dataX[0:train_size]), np.array(
dataX[train_size:len(dataX)])
trainY, testY = np.array(dataY[0:train_size]), np.array(
dataY[train_size:len(dataY)])
#input place holders
X = tf.placeholder(tf.float32, [None, seq_length, data_dim])
Y = tf.placeholder(tf.float32, [None, 1])
#build a LSTM network
cell = tf.contrib.rnn.BasicLSTMCell(
num_units=hidden_dim, state_is_tuple=True, activation=tf.tanh)
outputs, _states = tf.nn.dynamic_rnn(cell, X, dtype=tf.float32)
Y_pred = tf.contrib.layers.fully_connected(
outputs[:, -1], output_dim, activation_fn=None)
#cost/loss
loss = tf.reduce_sum(tf.square(Y_pred - Y)) # sum of the squares
#optimizer
optimizer = tf.train.AdamOptimizer(learning_rate)
train = optimizer.minimize(loss)
#RMSE
targets = tf.placeholder(tf.float32, [None, 1])
predictions = tf.placeholder(tf.float32, [None, 1])
rmse = tf.sqrt(tf.reduce_mean(tf.square(targets - predictions)))
with tf.Session() as sess:
init = tf.global_variables_initializer()
sess.run(init)
#Training step
for i in range(iterations):
_, step_loss = sess.run([train, loss], feed_dict={
X: trainX, Y: trainY})
print("[step: {}] loss: {}".format(i, step_loss))
#Test step
test_predict = sess.run(Y_pred, feed_dict={X: testX})
rmse_val = sess.run(rmse, feed_dict={
targets: testY, predictions: test_predict})
print("RMSE: {}".format(rmse_val))
#Plot predictions
plt.plot(testY)
plt.plot(test_predict)
plt.xlabel("x")
plt.ylabel("Sin(1.0/x)")
plt.show()
