Hi. In this math post I cover the topic of geometric sequences.

<center><img src="https://cdn.pixabay.com/photo/2015/05/31/13/41/calculator-791831_960_720.jpg" /></center>
<center><a href="https://cdn.pixabay.com/photo/2015/05/31/13/41/calculator-791831_960_720.jpg">Pixabay Image Source</a></center>

Screenshots are from witeboard.com with the use of my Wacom tablet & stylus.

## Topics
---

* Examples Of Geometric Sequences
* Geometric Sequence Formula
* Examples Of Solving For Missing Numbers In Geometric Sequences

&nbsp;

## Examples Of Geometric Sequences
---

To start here are a few examples of geometric sequences.

**Example One**

`2, 4, 8, 16, 32, 64, 128`

This sequence starts with 2 and doubles to obtain the next number until the last & seventh term of 128. Doubling is the same as multiplying by two. As the doubling is constant the common ratio here is 2. 

&nbsp;

**Example Two - Divide By 10**

`90000, 9000, 900, 90, 9, 0.9, 0.09, 0.009`

The first term here is ninety thousand. Obtaining the next number in the sequence involves dividing by 10. Dividing by ten is also the same as multiplying by one tenth. The common ratio here is `1/10` or `0.1`. There are eight terms in this geometric sequence.

&nbsp;

## Geometric Sequence Formula
---

There is a formula for representing any number in a geometric sequence. In text form it is `t_{n} = t1*(r)^(n-1)`. The n-th term is represented by `t_{n}`, the first term is represented by `t_{1}`, `r` is the common ratio and `n` is the number of terms. Screenshot shown below.


![geometricSequence_formula.PNG](https://images.hive.blog/DQmTgqWKTy7cK4ukg2SzZMydzBwk4m75SCoPJ49nuR59YJn/geometricSequence_formula.PNG)

&nbsp;

## Examples Of Using The Geometric Sequence Formula
--- 

**Example One**

The common ratio in a geometric formula is 3 and the first term is `1/27`. What is the fifteen term in this sequence?

With this question you have `r = 3`, `t_{1} = 1/27` and `n = 15`. Use the geometric sequence formula to obtain the fifteen term.


![example01.PNG](https://images.hive.blog/DQmP45bgw9Tb4upXuWvmceSsgtFPvV4dFc9edXGGG2SeRJ8/example01.PNG)


&nbsp;


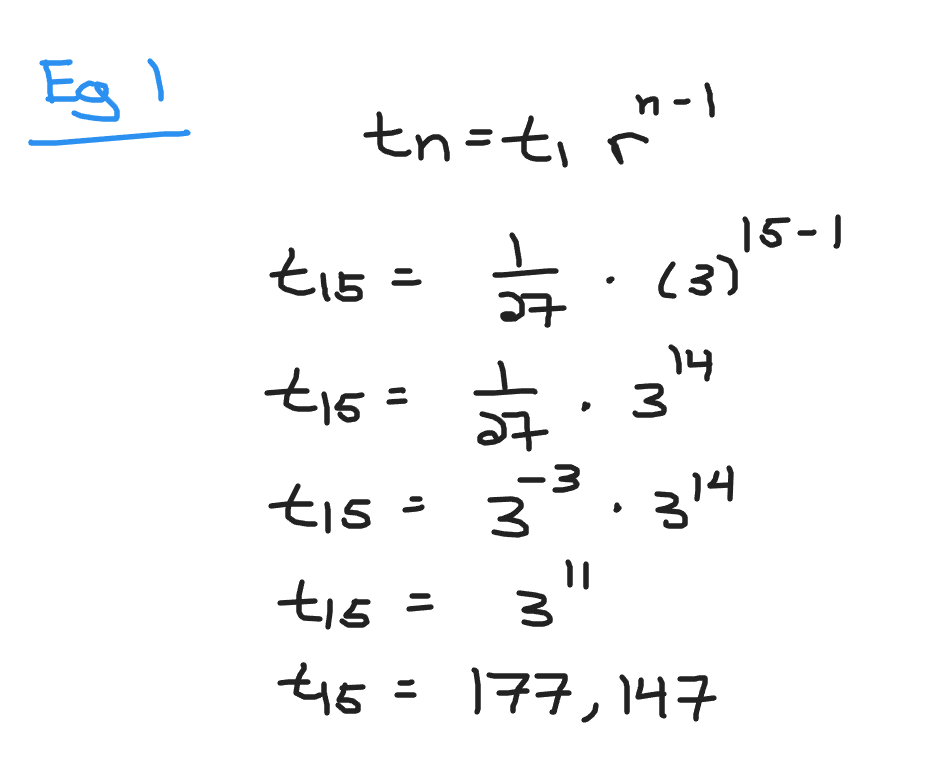
**Example Two**

In this geometric sequence the starting number is `0.0001` with a common ratio of 10. How many terms are there from the starting number to one billion (1,000,000,000)?

The common ratio gives `r = 10`, `t_{1} = 0.0001` and `t_{n} = 1 000 000 000`. Use the geometric sequence formula with the known values and solve for `n`. Note that one billion is ten to the power of nine.


![example02.PNG](https://images.hive.blog/DQmcY6Q3UDcLu3wUSqTYff49j7ryR22XYDeTtgj94hWdkSk/example02.PNG)


&nbsp;

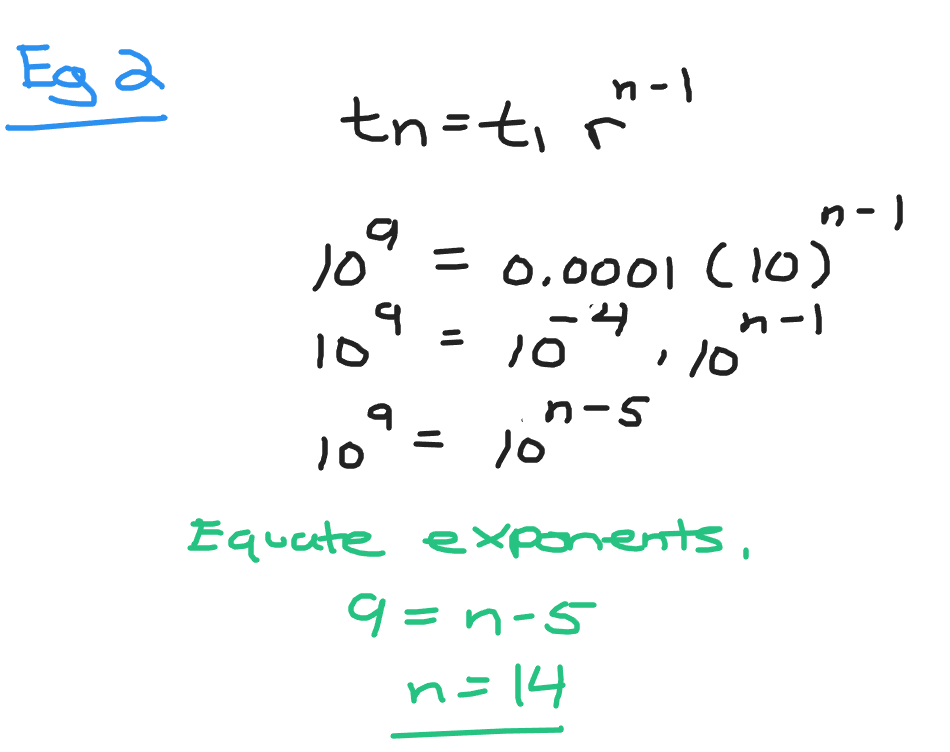
**Example Three**

There are sixteen numbers from 1 to 32768 in a geometric sequence. What is the common ratio here?

The starting number is `t_{1} = 1` and the last number is `t_{15} = 32768`. 

![example03.PNG](https://images.hive.blog/DQmSyGDTkvdgMSYLLfyerBaC5zMC1g3md4m4cLzXQcnoS5r/example03.PNG)

&nbsp;

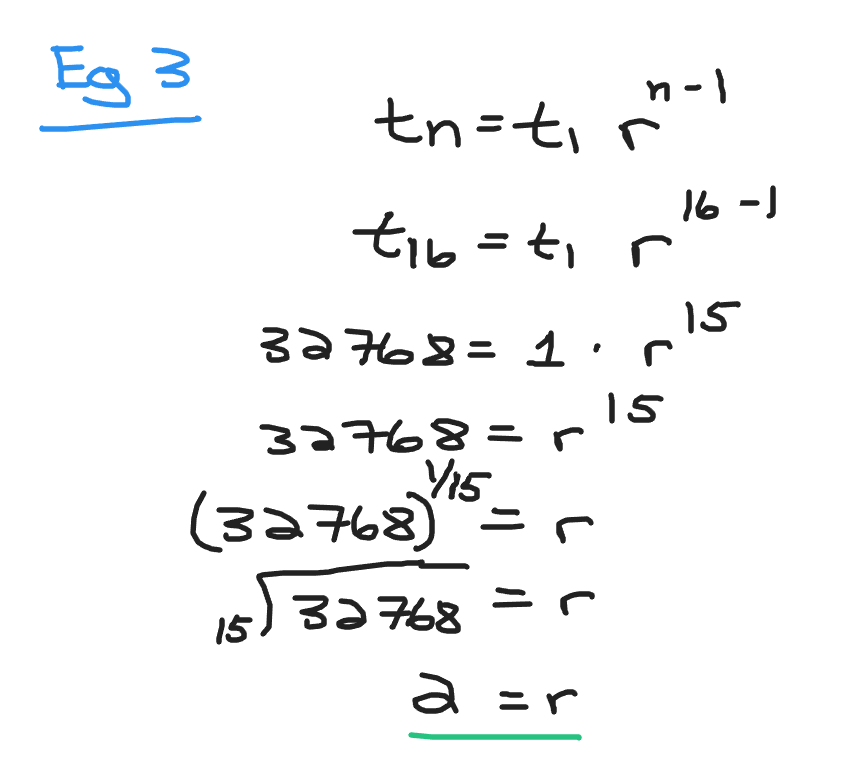
<center>Thank you for reading.</center>

Posted with [STEMGeeks](https://stemgeeks.net)