A modo de introducción
=
<div class=text-justify>La teoría de conjunto debe su aparición, en el mundo de la matemática, a ilustres personajes como, sin duda, lo fueron Georg Cantor, Richard Dedekind y Gottlob Frege.

--------

<center>![CANTOR.jpg](https://cdn.steemitimages.com/DQmZ4KDrQyK8fwcVw4Khkk7wczcLkg5iTnAibaQW2uK3NYi/CANTOR.jpg)</center>
<center>[link](https://cdn.steemitimages.com/DQmZ4KDrQyK8fwcVw4Khkk7wczcLkg5iTnAibaQW2uK3NYi/CANTOR.jpg)</center>

 En un primer momento, lo relativo a la teoría de conjunto fue visto con cierta reservas, desconfianza y aversión dentro del ambiente matemático  ya establecido, sin embargo, con el correr del tiempo la teoría de conjunto, por su ***considerable importancia en ramas de la matemática como la topología y la teoría de funciones***, ha alcanzo un papel preponderante en el escenario de la Matemática Moderna resultando un absurdo, actualmente , hablar del desarrollo de las matemáticas sin considerar el aporte que  se ha logrado desde la teoría de conjuntos. 

En este contexto, en este primer post, respecto a la teoría de conjuntos, vamos a abordar lo relativo a la ***idea de conjunto y elementos, formas de determinar un conjunto, pertenencia y no pertenencia y la definición de conjuntos finitos y no-finitos***. Iniciemos, acompáñenme!!

Elementos y conjunto
=
Al iniciar el estudio de la teoría de conjunto debemos hacerlo partiendo por dos ideas fundamentales, a saber, conjunto y elementos. 

<center>![recorte conjunto.PNG](https://cdn.steemitimages.com/DQmSXe3SF8ZMdWGGkwc9pWNNwALCGpoqEb4xAgCosfvx57P/recorte%20conjunto.PNG)</center>

-----

<h4>Ejemplos:</h4>

***Las hojas de un cuaderno. los puntos de una recta, las rectas de un plano, los números naturales***.

-----

A su vez, ***cada uno de los objetos del conjunto es un elemento***.

***Los conjuntos los representamos con letras mayúsculas***: A, B, C, …, etc., y ***a los elementos con letras minúsculas***: a, b, c, …, etc.

Determinación de un conjunto
=
Los conjuntos, en matemática, los podemos determinar por extensión y por comprensión.

<center>![Determinacion.PNG](https://cdn.steemitimages.com/DQmQzAGJBKkfMke3DtXiMyWSjAn8cY5aEWeequLDqArML5U/Determinacion.PNG)</center>

------

<h4>Ejemplos:</h4>

------

1.- El conjunto A cuyos elementos son 1, 3, 5 se representa así:

   A={1,2.3}

2.- El conjunto B de los múltiplos de 5 se representa así:

  B={múltiplos de 5}

-----

En el ejemplo  1, el conjunto A está determinado por extensión, pues se han enumerado todos los elementos del conjunto. Por otro lado, en el ejemplo 2, el conjunto B está determinado por comprensión, pues se ha enunciado la propiedad que caracteriza sus elementos.

-------

Pertenencia y no pertenencia
=

<center>![pertenencia3.PNG](https://cdn.steemitimages.com/DQmbBWr2WAMdxEwZXk6mqxEVSPHnqEWtvBnBvt9eC3TXXAK/pertenencia3.PNG)</center>


-------

  <h4>Ejemplos</h4>

-----

La proposición:

“Venezuela (v) pertenece al conjunto de las naciones americanas (A)”,  se representa así: 

***v ∈ A***

-----

Por otro lado, la proposición:

“Alemania (a) no pertenece al conjunto de las naciones americanas (A)”, se representa así:
          ***a ∉ A***

-------

Conjuntos finitos y no-fintos
=

----

<center>![Finito y no-finito.PNG](https://cdn.steemitimages.com/DQmQDFFXCxwsFFXfTvUHb3841RZYTjZ9ncvDqk5Hhf3Uuns/Finito%20y%20no-finito.PNG)</center>

-----

<h4>Ejemplos:</h4>

-----

Los conjuntos:

------

<center>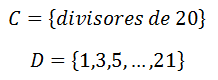![EJEMPLO FINITOS.PNG](https://cdn.steemitimages.com/DQmTC18ppMyXPwhTUGEsNCfAhKeBvTxgtLgap3x1rBvm4oL/EJEMPLO%20FINITOS.PNG)</center>

------ 

son conjuntos finitos, pues en cada caso sabemos cuales son todos sus elementos desde el primero hasta el último.</div>

-----

Por otro lado, los conjuntos:

------

***N={0,1,2,3,4,…}***

-----

***R={puntos de una recta}***

-----

***D={polígonos del plano}***

------

Son conjuntos no-finitos.

-----

> ***Hasta acá nuestro primer post, de dos que dedicaremos a la Teoría de Conjuntos, les invito a seguir acompañándome***.