<div class=text-justify>Hola amig@s, por razones ajenas a mi voluntad, debí, por unos días, suspender mis publicaciones en esta fabulosa plataforma, hoy quiero retomar nuestro contacto con un contenido vinculado  a  mi área de formación, la matemática.

-----

Superado el contratiempo, les invito a seguir un estudio constructivo de este bello mundo matemático que hoy retomamos a partir de un tema esencial y muy importante como lo es, sin duda, lo relativo  al ***Sistema de los Números Naturales***. Abordaremos, en este post, ***su definición y  axiomas de caracterización*** , mientras dejaremos para una próxima publicación un ejemplo ilustrativo de la verificación  del sistema axiomático, que seguidamente abordaremos.

------

<center>![numeros.gif](https://cdn.steemitimages.com/DQmdsEbUsweohvSFCAWvRTLeFaKiZJQYpettwojcMGPsVGP/numeros.gif)</center>
<center>[link](https://cdn.steemitimages.com/DQmdsEbUsweohvSFCAWvRTLeFaKiZJQYpettwojcMGPsVGP/numeros.gif)</center>

------

Definición
=

Desde un punto de vista empírico tenemos conciencia de los números naturales desde muy temprano en nuestras vidas. Cuando ya cursamos los primeros años de escolaridad empezamos a tener contacto con los números naturales, allí se nos dice que son los empleados para contar, empezamos a saber que ese mecanismo a través del cual emparejamos las cosas con un símbolo, corresponde a la utilización de los números naturales.

-------

En la escuela, así, comenzamos asociar la idea de números naturales con la letra ***N***, utilizada para representar a una ***agrupación*** que  llamaremos ***El Conjunto de los Números Naturales***,  en el cual se concentran esos primeros símbolos matemáticos, los números, con los cuales empezamos a entrar en contacto con la realidad de una manera formal, ideal, conceptual.

-------

<center>![numeros2.jpg](https://cdn.steemitimages.com/DQmUuxQq9pgPgDuM3aZvpmZ17PmCNXYz75yUpT4uC47CqMF/numeros2.jpg)</center>
<center>[link](https://cdn.steemitimages.com/DQmUuxQq9pgPgDuM3aZvpmZ17PmCNXYz75yUpT4uC47CqMF/numeros2.jpg)</center>

------


Empanzamos a extender nuestro lenguaje y podemos sustituir, si queremos, la expresión "dos naranjas" por "2 naranjas"  y, de igual manera, un gran números de naranjas, o  cualquier otro grupo de objetos,  puede ser identificado con un símbolo para diferenciarlo de cualquier otra agrupación  de objetos, de la misma índole,  que se diferencian en la cantidad  de  unidades que conforman los  grupos en cuestión. ***En resumidas cuentas, nuestro primeros pasos matemáticos los damos a partir de los números naturales pues la primera  operación que hacemos con conciencia matemática es contar y eso lo hacemos gracias a los Números Naturales***.

---------

Sin embargo, a nivel de la formalidad matemática podemos dar una  definición, un poco más abstracta y compleja, respecto a ese conjunto que inicialmente, en nuestros primeros pasos, utilizamos para contar. En este sentido, vamos a referirnos , ahora a nivel general, al Sistema de los Números Naturales para abarcar la generalidad y formalidad que, a través del álgebra moderna, podemos obtener para robustecer y ampliar nuestra cultura respecto a los números naturales. 

Vamos entonces a referir, desde el Álgebra Moderna, ***la definición del Sistema de los Números Naturales***, entendido como un sistema axiomático:

***El sistema axiomático*** de los Números Naturales se representa por el par ***(N, s)***, donde ***N es un conjunto y "s" es una función***. El conjunto N está formado por elementos "n" que llamaremos números naturales. Por su parte , s es una función de N en N, donde la imagen de cada elemento de n, a través de s, recibe el nombre ***de sucesor de n*** , mediante s. 


Esquema ilustrativo:



-------

<center>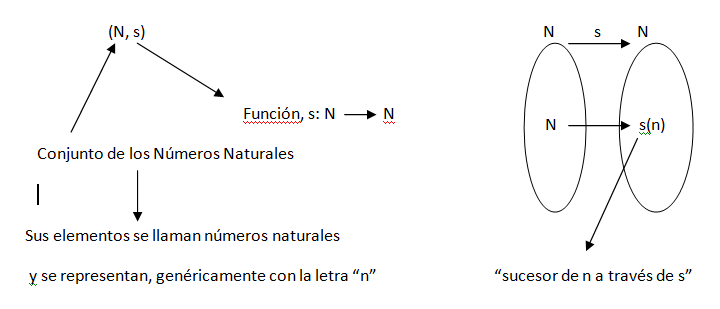![Ilustacion.PNG](https://cdn.steemitimages.com/DQmP5rknYBbDevRfyKBPt3bfkbaizZFPh4hqnSXsMGqRNyo/Ilustacion.PNG)</center>


-------


El sistema axiomático de los números naturales , a propósito de permitir la construcción de los elementos de N, verifica los siguientes axiomas: 

1. ***La función  s  es inyectiva***, es decir: 

      <center>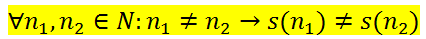![inyectiva.PNG](https://cdn.steemitimages.com/DQmXwkqLGD8MXYSWiMn2yGk4SPXXbTiQYczH2RDnBMmVUSv/inyectiva.PNG)</center>


 2. ***La función s no es sobreyectiva***, ya que existe en N , un número llamado cero "0", que no es sucesor de ningún otro n mediante s, es decir, 0 no forma parte del conjunto imagen de s.

------------



<center>![no sobreyectiva.PNG](https://cdn.steemitimages.com/DQmQmDwaFFvVpZU1LfWpTLR5mp9Facgk5wnJ686oCdnN6QX/no%20sobreyectiva.PNG)</center>


-----


3.- Si una propiedad inductiva   la tiene un primer elemento "0" entonces la tienen todos los números naturales. es decir:

-------

<center>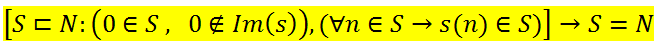![Inductividad.PNG](https://cdn.steemitimages.com/DQmdGXgWigzkg3FtdNeooh5k9TJuRU6bv7SzgaQkat7P6gJ/Inductividad.PNG)</center>


-------


***Nota***: Una propiedad que pueden tener los número naturales es inductiva si al tenerla un número natural entonces, necesariamente la tiene sus sucesor.

-------


Como reconocemos que muchos aspectos pudieran quedar fuera del alcance de algunos lectores, en el siguiente post haremos referencia a la idea de función íntimamente ligada a la definición del Sistema de los Números Naturales. ***En este sentido, el  manejo de las funciones será muy valioso para ayudar a cubrir cualquier vacío que pudiese haber quedado en la descripción que, hasta aquí, hemos desarrollado***. Posteriormente, en otro post, ilustraremos el sistema de los números naturales a través de una demostración, característica esencial del trabajo en álgebra moderna</div>