<div class=text-justify>Hola amigos, quisiera compartirles, por algún tiempo,  una serie de contenidos referidos al álgebra. En este sentido, quisiera comenzar hoy  por una aspecto básico denominado Ley de composición  interna. Este contenido nos permitirá, luego, abordar aspectos, del álgebra moderna, de mayor complejidad como, por ejemplo,  lo son las estructuras algebraicas:  grupos, anillos, cuerpos y los espacio vectoriales. Esto último de suma interés para la ciencia y la tecnología actuales por la vasta cantidad de aplicaciones que de aquellas se desprenden.

-------

<center>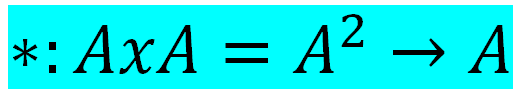![lci def.PNG](https://cdn.steemitimages.com/DQmXeQstrYeWLga7jh7SzsgZF6czdZPzXoQb1jwe2MGaybB/lci%20def.PNG)</center>


------



Ley de Composición interna. Definición
=
Una ley de composición interna definida en un conjunto no vacío A, consiste en una operación que asigna a cada par ordenado de elementos de A un único elemento de A. Lo anterior significa que a cada elemento de AxA le corresponderá un único elemento de A.

<h2>Definición</h2>
Ley de composición interna definida en un conjunto no vacío A, es toda función de AxA en A. La ley de composición interna la denotamos con el símbolo *

<h2>Simbólicamente</h2>

<center>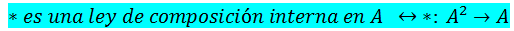![lci 1.PNG](https://cdn.steemitimages.com/DQmeFEcWNG3PHuumWc45tQXeQBpwyMWkw9qcAq89qFTu5bi/lci%201.PNG)</center>

Es decir:

 <center>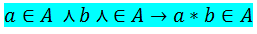![lci 2.PNG](https://cdn.steemitimages.com/DQmaEugjdTC2vgyQAijcXskNUMQNUZYGktLjwk9y1wx9LUU/lci%202.PNG)</center>

Debe quedar entendida la unicidad por que recuerden que * es una función, por definición, es decir, si la imagen existe ésta es única.

-----




***Son ejemplos de leyes de composición interna la adición y la multiplicación en los naturales (N), los enteros (Z), en los racionales (Q), etc. Si sumas, o multiplicas , 2 naturales el resultado será otro natural, lo mismo sucede en Z y en Q, y en general en R*** (conjunto de los números reales).

Las siguiente tabla de doble entrada define una ley de composición interna en el conjunto A.

<center>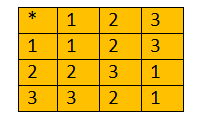![tabla.PNG](https://cdn.steemitimages.com/DQmWsiLBvCXiem3wgLZSLqDLvCAxxouz4KMSUUHZFdASNbL/tabla.PNG)</center>

---------

Nótese como cada par del producto AxA es un elemento de A. AsÍ, ,  1 * 1=1, 1 * 2=2, etc., es por ello que las leyes de composición interna, se les llama también ***leyes cerradas o de clausura*** 

Veamos un ejemplo más.

-----

<center>![EJEMPLO.PNG](https://cdn.steemitimages.com/DQmPjvrH6cU7SbSQQr5q32FNwc4hptN3ieKnYxPB6wRJj52/EJEMPLO.PNG)</center>

-----


En RxR se define * mediante  

  (a,b)*(c,d)=(a+c, b+d)

Esta es una ley interna llamada suma ordinaria de pares ordenados y se efectúa sumando en el conjunto de los números reales (R), componente a componente. Como cada par ordenado reales caracteriza un vector en el plano, con origen en sistema cartesiano, resulta que el significado geométrico esta ley de composición interna en RxR consiste en la diagonal del paralelogramo cuyos lados son los vectores dados, tal como se observa en la siguiente ilustración:</div>


<center>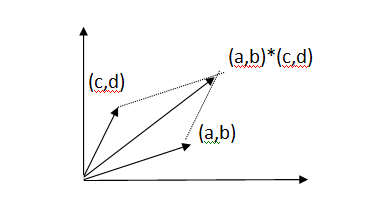![suma de vectores.PNG](https://cdn.steemitimages.com/DQmNii6dtPLwDGrPujyGSzWB8jriYWEEYxZrrcbaAx27J6q/suma%20de%20vectores.PNG)</center>

-------

> ***Buenos amigos hasta acá nuestro contenido del día, en nuestra próxima publicación empezaremos a abordar las estructuras algebraicas. Hasta entonces...***



<h2>Biblografía</h2>

***Rojo A. (1996). Algebra I. Editorial Ateneo. Argentina***