Matrices 2. Operaciones
spanish·@josmar2511·
0.000 HBDMatrices 2. Operaciones
<div class=text-justify>Hola mis estimados amigos. Bienvenidos, nuevamente, a nuestro rincón matemático, les invito a un nuevo paseo por el mundo de las matrices. En esta nueva oportunidad, les quiero compartir lo referido a las operaciones con matrices. Sin más, comencemos nuestro acostumbrado recorrido. ------- <center>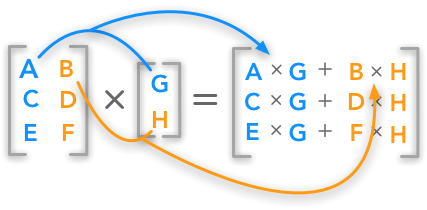</center> <center>[link](https://cdn.steemitimages.com/DQmVD6ZHAUYpPvKC7KZwNsoNcC86DPRyLdfMKQkatcfNZb7/portada.png)</center> ------- <h1>Operaciones con matrices</h1> ------ Antes de iniciar, de manera específica, con las operaciones entre matrices, resulta oportuno señalar lo que tiene que ver con la igualdad de matrices, en este sentido, referimos: ---- <center></center> ------ O sea: (aij) = (bij) si y sólo si aij = bij para cada i y para cada j. --------- Ahora si, vayamos a las operaciones con matrices. <h1>1.- Suma de matrices</h1> ------ Sean (aij) y (bij) dos matrices del mismo orden mxn. La matriz suma se obtiene, genéricamente, como se indica: Sumamos: (aij) + (bij)= (aij + bij) ------ <center></center> ----- <center></center> ------- <center>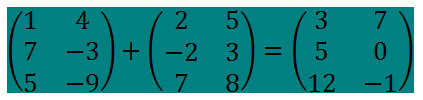</center> ----- <h1>2.- Multiplicación de una matriz por un número</h1> ------ Sean (aij) una matriz de orden mxn y r un número real. Definimos el producto de r por la matriz (aij) como se escribe a continuación: ----- Nótese : r . (aij) = (r.aij) ------ <center></center> ---- <center></center> ------ <center>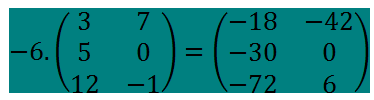</center> ------ <h1>3.- Multiplicación de matrices</h1> ----- Inicialmente, debemos reconocer que no todas las matrices pueden multiplicarse. Es necesario que la matriz que cumple la función de ser el primer factor sea de orden mxn y la segunda matriz, segundo factor da la multiplicación, sea de orden nxp; dicho de otra manera, sólo se pueden multiplicar dos matrices cuando el número de columnas de la primera matriz que multiplica coincide con el número de filas de la segunda matriz. Así, la matriz resultante sera de tamaño , u orden, mxp. ------- <center></center> ---- <center></center> ----- Supóngase que, los consumos anuales de 4 familias X,Y, Z y T en fruta, pescado y queso vienen dados por la matriz A. Los precios de esos mismos productos en los años 1993 y 1994 venían dados por la matriz B. ----- <center>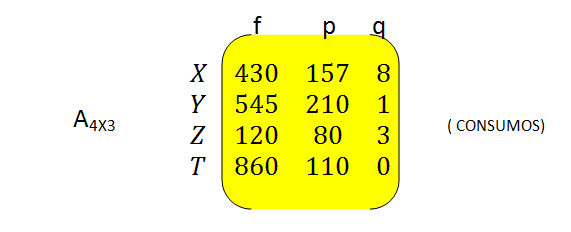</center> ----- <center>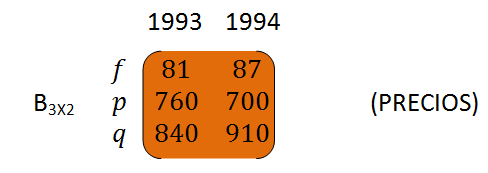</center> ----- La matriz A.B nos dará el gasto en frutas, pescado y queso de cada familia por año, así: ----- <center>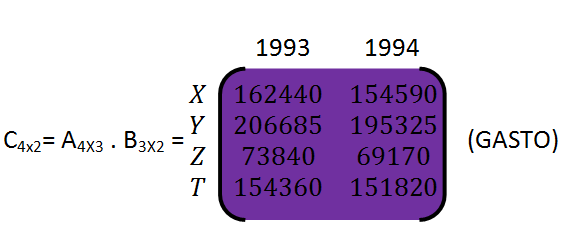</center> ----- Así, por ejemplo, podemos afirmar que la familia Z gastó 73840 bolívares en fruta, pescado y queso en 1993. Mientras que la familia X, en 1994, gastaba 154590 en los mismo 3 alimentos, antes referidos. -------- Veamos, ya para concluir, a modo de afianzar el cálculo del resultado, cómo se obtuvo, por ejemplo, el elemento c11= 154590 de la matriz gasto.</div> ----- <center></center> ------ > ***Bueno amigos, si me han acompañado hasta acá, muchas gracias. Nos vemos en próximo encuentro donde la matemática y steemit, serán, nuevamente, protagonistas. Saludos!!***
👍 eforucom, supu, xyzashu, minminlou, theclub, josmar2511, vensport, soredesi, fredhm, gmart, arausi, yasfer, bouderleire, jeanette38, fotoven, poetavzla, xofia, relatos, panavenezolano, infantiles, efemerides, solmar, vensports, sportsven, newsport, fullnews, poemario, ciroeskandar, minnowsupport, shaniaa01, ramonycajal, cervantes, gargon, purapapita, wilsonlozano, pgarcgo, jgcastrillo19, dulcinea, wartrapa, titin, nelyp, cuvi, elfictron, gabox, teo, lrsm13, fnux, simonmaz, maastro, dayana82, garvi, phaazer1, albagargon, credlonu, yooerlyn, waldo22, mdcomes, yuslindwi, yessenia, noticias, aidnessanchez, davidcentenor, davidcurrele, arepaleaks, arepa.exe, javyeslava.photo, investigate, wilkynson, joso, velazquezboy, reinaseq, lizdeluca, josuepalacios, tsoldovieri, reimerlin, artemisjane26, dechastre, perniachiquito, edwinbasu, tokengold, jkj, spanishchef, maticpecovnik, dcardozo25, sweetdesserts, sophiegeek, reinaldoverdu, sayago, biteosdev, adonisr, angoujkalis, kaux, neymarjr, cyprianj, roinv, steeming-ali, jessiearias, ratspencer, electrodo, arnaldoropeza, patris, ibiza, hijosdelhombre, aneblueberry, magoia, heiditravels, teacher, luisucv34, delegate.lafona, kilianmiguel, fidel-castro, mpandrew, lenin-mccarthy, mariacherries, hectgranate, florharys, soymanu, freecreative, kranga, dinocreative, blocktrades, mys, beleg, imperfect-one, trans-juanmi, jdevora, birresth, darkstar1o9, bohemian.machine, zackarie, carlosrada, josefelix, alex-hm, donasys, wackou, elnefelibato, julian.alejandro, rubedarioh, mike961, coquiunlimited, inedido, edgarjbb, desikaamukkahani, opheliapoe, goodway, rococo20, wolfvanween, rafarosado, soledadjc, boykeren, edu-venezuela, cindycam, deisip67, roseri, lasocia, carmenl,