Mínimo común múltiplo y Máximo común divisor
spanish·@josmar2511·
0.000 HBDMínimo común múltiplo y Máximo común divisor
<div class=text-justify>En el camino de los Naturales a los complejos en el cual ya hemos dado dos pasos muy importantes, los Naturales y los Enteros, nos acercamos cada vez más a un conjunto sumamente importante los Racionales, las fracciones. Sin embargo, hemos abierto un paréntesis que nos ha llevado a algunos aspectos previos y necesarios para estudiar mejor a los racionales. ------ Así hablamos, en la publicaciones anterior, [divisibilidad](https://steemit.com/spanish/@josmar2511/divisibilidad), de los números primos y compuesto , como también de los criterios de divisibilidad. Siguiendo con esos fundamentos previos hoy le corresponde el turno a lo que seguramente recuerdan haber trabajado en su escuela básica, nos referimos al ***Mínimo Común Múltiplo (m.c.m) y al Máximo Común Divisor (M.C.D)***. ---- Antes de entrar, de lleno, a los aspectos anteriores recordemos la ***descomposición en factores primos***. ------ <center></center> <center>[link](https://cdn.steemitimages.com/DQmdaaJa7T7tEx1pgeWhWZJsKoyqy1hfo8YRYWSKDRMqv3J/mcm.jpg)</center> ------ <h1>Descomposición en factores primos</h1> ------ <center></center> ------ Para ello, se divide el número por el menor de sus divisores que sea un número primo. Luego, el cociente obtenido se vuelve a dividir por el menor de sus divisores que sea, igualmente, un número primo y así sucesivamente hasta obtener como cociente un número que sea primo. ------- <center></center> ----- Descomponer en factores primos 37.800: ------ <center>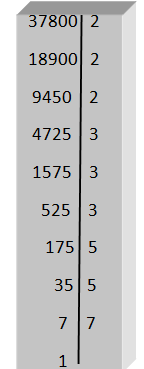</center> ---- Por lo tanto, podemos escribir 37.800 como un producto de factores primos de la forma siguiente: ----- <center></center> ------- <h1>Mínimo Cómún Múltiplo</h1> ------ <center></center> ------ ***Así, el mínimo común múltiplo, por ejemplo, de 6, 8 y 10 es 120, pues 120 es el menor múltiplo común de 6, 8 y 10, respectivamente***. ---- <h1>Cómo determinar el m.c.m</h1> --- Para determinar el mínimo común múltiplo entre varios número dados, simplemente ***descomponemos dichos números en sus factores primos y de dichos factores tomamos los comunes y no comunes con su mayor exponente. Formamos un producto con la selección realizada y el resultado será el m.c.m buscado***. ----- <center></center> ------ Tomemos como ejemplo los tres números anteriores, 6, 8 y 10 y verifiquemos que el m.c.m es 120 aplicando, ahora, el procedimiento descrito. ------ <center>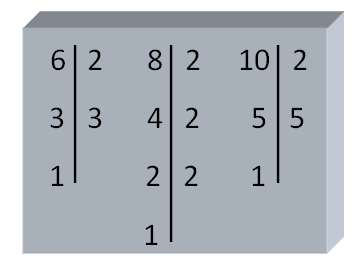</center> ------ Entonces: ----- <center>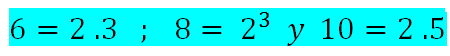</center> ------ Tomando, ahora, los factores comunes y no comunes elevados al mayor exponente, resulta: ----- <center>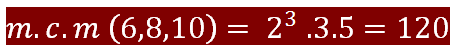</center> ------- <h1>Máximo Cómún Divisor</h1> ---- <center></center> ----- Así, por ejemplo, ***si consideraos, nuevamente, los números 6, 8 y 10, tenemos que el M.C.D, entre dichos números es 2***, pues es el 2 el mayor divisor común existente entre 6, 8 y 10. ---- <h1>Cómo determinar el M.C.D</h1> ---- Para determinar el máximo común divisor entre varios números, descomponemos dichos números en sus factores primos. De dichos factores seleccionamos solamente los factores comunes y el producto de dichos factores será el M.C.D buscado. ----- <center></center> ------- Tomemos, nuevamente, como ejemplo los ***tres números anteriores, 6, 8 y 10 y verifiquemos que el M.C.D es 2*** aplicando, ahora, el procedimiento antes descrito. ------- <center></center> ------ Entonces: ----- <center>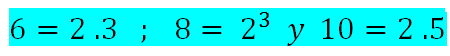</center> ----- Luego, al seleccionar los factores comunes, con el menor exponente, resulta: ----- <center></center> ------ Nótese, que ***solamente el 2 un factor común entre los tres números seleccionados y sólo debemos considera el de menor exponente***, como ya lo habíamos resaltado. ------ Bueno amigos, hasta acá nuestra publicación del día. Ahora, ya estamos preparados para, en nuestra próxima publicación, empezar conocer debidamente al conjunto de los números racionales.</div> ---- > .***..Hasta entonces!!***
👍 maulid, steeming-hot, votes4minnows, laissez-faire, marina007, jadabug, samotonakatoshi, ezravandi, hdu, imisstheoldkanye, delabo, hankoeok, accelerator, josmar2511, vensport, team, fredhm, gmart, soredesi, arausi, yasfer, bouderleire, jeanette38, fotoven, poetavzla, xofia, relatos, panavenezolano, infantiles, efemerides, solmar, vensports, sportsven, newsport, fullnews, poemario, ciroeskandar, minnowsupport, ylich, shaniaa01, delpilar, sergiopocasluces, la-colmena, curie, aidarojaswriter, gabriellecd, rafartista, milkabustamante, bohemian.machine, gabyoraa, felixjfarfan, aumonde, yisusgtr, emperorhyspania, jimmyvidal, stimu, duocover, salvadorhr18, aullidodecisne, el-panal, elelobos, javierh95, arar5, fantastictwins, iamsaray, naturalbornk, liberosist, ascorphat, vact, diebaasman, aboutyourbiz, cryptokrieg, reaverza, trixie, chrisluke, dashfit, locikll, hotsteam, pinksteam, skycae, gunboat, ninjace, zipporah, c-squared, anwenbaumeister, operahoser, hiddenblade, niouton, schroders, hendrikdegrote, clweeks, kendallron, moksamol, choogirl, jayna, ggd3yydze, cepul, joendegz, stahlberg, mattiarinaldoni, lazybird, alexworld, sarez, hansmast, didic, tombstone, neumannsalva, drmake, avizor, whoib, clement.poiret, javier.dejuan, gabrielatravels, ilovecryptopl, lola-carola, mininthecity, psygambler, gmedley, edjesus, gordon92, reizak, zlatkamrs, teukurival, kenadis, maticpecovnik, bflanagin, trang, eu-id, lekang, allcapsonezero, dokter-purnama, onemedia, ambitiouslife, travisung, revo, eurodale, cryptononymous, shayekh2, reverseacid, nicephoto, zerotoone, tensor, aaronleang, joshman, cryptocopy, breakout101, epic4chris, reitsportdokus, photographybd, theinspiration, yaelg, arcange, raphaelle, mindstabber, anatere, isisvima, peaceandwar, thecastle, thescubageek, doifeellucky, historiasamorlez, wackou, drifter1, alvin0617, electrodo, juanhlb, cryptofuwealth, longer, sumotori, torico, mrbarckhoff, jiujitsu, danaedwards, shinedojo, gracelbm, combatsports, steemph.manila, rye05, massivevibration, mammasitta, rival, macoolette, eric-boucher, nicole-st, yomismosoy, goodway, kafupraise, jbrrd, xanderslee, faithfullwills, lk666, oghie, ivan-g, gpcx86, yashshah991, wilmer14molina,