# Introduction
 저는 **대수기하학** 및 **정수론** 을 블로그에서 심도깊게 다루는 것을 최종 목표로 하고 있습니다. 

내용이 어렵기도 하고 다양한 수준의 독자들을 고려해야 하기 때문에 기본적인 대수학 강의를 먼저 할 예정입니다. 위에 언급한 분야들을 연구하기 위해서는 **선형대수학, 실해석학, 복소해석학, 대수학, 위상수학, 미분기하학** 등의 선수 지식들이 필요한데, 필요하다면 위상수학 정도는 포스팅 해 드릴수 있습니다. (하지만 그림 그리기 귀찮아..)

강의글을 쓸 때 증명을 정말 세세하게 할지 생각했는데 생각해보니 의미가 없는거 같아요. 어짜피 공부는 책으로 하는거고 좋은 reference 들이 많으니.. 그래서 수학 토막상식 (이라고 하기엔 어려울지도..)을 전달하고 수학적 흥미를 유발한다는데 의미를 두고 포스팅을 할 것 같아요.

Steemit Markdown은 Latex 가 지원이 안되네요.. 왠만한 equation 이나 statement 는 그냥 특수문자로 쓰고, diagram 은 Latex 코드를 이미지 파일로 rendering 해서 첨부 할거에요.

잡설이 길어지네요. 아무튼 시작합니다.

### 본론에 들어가기 앞서:
수학에 관심이 있다면 영어를 잘하는게 중요하거든요. 좋은 reference 들은 죄다 영어, 프랑스어, 등등.. 외국어를 잘하는게 중요해요. 그래서 우선 영어로 설명하고 한국어로 후술 하는 방식으로 할게요.

일단 독자분들이 **function** (함수) (sometimes it is called a **map** or **mapping**. 저는 *map* 이라는 표현을 더 좋아해요) 이나 **set** (집합) 이 뭔지 알고 있다고 가정할게요.
∃ 는 'there exists (~가 존재한다,존재해서)',  ∀ 는 'for all (모든 ~에 대해서)' 이라는 뜻이고, *s.t.* 는 such that 의 축약어 입니다.

## What is  a **Group**?
일단 독자분들이 **function** (함수) (sometimes it is called a **map** or **mapping**. 저는 *map* 이라는 표현을 더 좋아해요) 이나 **set** (집합) 이 뭔지 알고 있다고 가정할게요.
오늘은 대수학의 기본중의 기본인 **Group theory** (군론)에 대해서 강의를 하겠습니다. 수학 물리 등등 많은 분야에서쓰이는 개념입니다. 오늘은 **Group** (군)의 정의와 간단한 예시를 배워봅시다.

자, Group을 정의 해 보겠습니다.

### Definition of a Group:
![ql_e10850539de50538dbe4d19510891ce8_l3.png](https://steemitimages.com/DQmRA5DSm1a2wT3hgb1jPbjHvjHshyW7FyAQ1zgrvoKx6MX/ql_e10850539de50538dbe4d19510891ce8_l3.png)

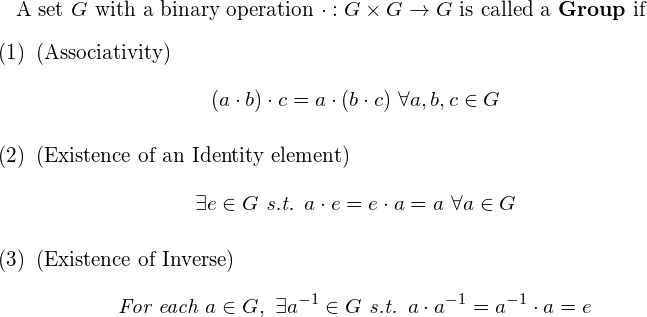
이게 무슨 소릴까요.. 벌써부터 혼란스러운 독자분들을 위해 각각의 항목에 대해 설명 드리겠습니다. 첫번째로,  
>A set *G* with a binary operation · : *G×G→G*

라는 표현이 있는데요, binary operation · : *G×G→G* 이라는 것은, 집합 *G* 위에서 이루어지는 **이항연산(두개의 항을 연산한다)**을 의미해요. 

(*G×G* 는*G*의 *Cartesian product* 입니다. 쉽게 말해서 *G*의 모든 순서쌍(ordered pair)들의 집합이죠.)
>*G×G*={(*a,b*)| *a,b*∈*G*}

다시 말해서, '이항연산'이라는 표현은 집합 *G*에 있는 '두개의 원소'를 뽑아서 연산을 하면 *G*에 있는 '하나의 원소'가 된다는 것이에요.

쉬운 이해를 위해 예시를 들어볼게요. ℤ를 모든 정수들의 집합으로 정의하고,
> ℤ={···,-2,-1,0,1,2,···})

 \+ 를 우리가 잘 알고있는 덧셈 (usual addition) + 로 정하겠습니다. + 는 두개의 숫자를 더하는 연산이죠. 다시 말해서 **두 숫자의 순서쌍을 다른 숫자로 보내주는 함수**입니다. 그러면 +는 ℤ×ℤ 위에서 정의된 ℤ로 가는 함수가 되고 따라서 ℤ 위에서의 이항연산이 되죠. 예를 들어, +는 (2,3)을 5로 보내줍니다. (2+3=5 의 재해석..)

마지막으로 위의 Group 정의에 나와있는 1, 2, 3번 조건들은 각각 **결합법칙, 항등원의 존재성, 역원의 존재성** 인데요, 다들 고등학교 수학시간에 배웠으리라고 생각해서 자세한 설명은 안할게요. 

이것도 마찬가지로 예시를 들어서 설명하는게 이해가 빠를거 같아요. 위에서와 마찬가지로 ℤ에 대해서 생각해 보죠.  정수 *a,b,c*∈ℤ 에 대하여
>(a+b)+c=a+(b+c) (결합법칙; 예: (2+3)+5=2+(3+5)=10)
>0+a=a+0=a (덧셈에 대한 항등원은 0; 예: 0+2=2+0=2)
>a+(-a)=(-a)+a=0 (a의 역원은 -a; 예: 3+(-3)=-3+3=0)

가 성립하는 것을 알 수 있습니다.

Group (군)의 정의를 끝내기 전에, 몇가지 알아야 할 사실들을 짚고 넘어갈게요 (Remarks):

### Remark
*G* 가 연산 ·에 대하여 Group 이라고 하겠습니다. (또는, 이를 "(*G*,·) 이 Group이 된다"고 간략하게 쓰기도 합니다) 그럼 다음이 성립합니다:
>*G*의 항등원 *e*는 유일합니다 (e' 가 *G*의  또다른 항등원이라면, *e=e*' ).
>각각의 원소 *a∈G* 에 대하여 역원 *a*^{-1}는 유일합니다.

(둘 다 쉽게 체크 가능)

### Notation (표기법)
이항연산을 덧셈 +로 쓰면 +에 대한 역원(Inverse)는 -*a* 로 쓰고 (additive notation),
이항연산을 곱셈 ·으로 쓰면 · 에 대한 역원은 *a*^{-1} 로  주로 씁니다 (multiplicative notation).
(2의 덧셈에 대한 역원은 -2이고, 3의 곱셈에 대한 역원은 1/3이라고 표기하는 것을 생각해보세요. 당연하죠.)

### Remark
위에서 살펴본 바로 알 수 있듯이 모든 정수들의 집합 ℤ는 연산 +에 대해서 군이 됩니다! 이때 (ℤ,+) 가 군이 된다고 표현합니다. 

자, 생각보다 군은 쉽습니다, 유치원 때 부터 배워왔고 우리 생활 가까이에 있다는걸 알 수 있죠. 하지만 수학을 심각하게 공부해보면 어려운 군들이 많습니다.
다음 시간에는 군의 쉬운 예제들을 몇가지 들어보겠습니다.


### 이 글의 모든 저작권은 @kjs105 에게 있음을 알려 드립니다. 스크랩 시 링크 및 출처는 분명하게 해주세요.