# Introduction
저번 포스팅에서 정수 *n*에 대하여 ℤ/*n*ℤ 를 정의했었는데요, 아직은 우리가 quotient group 개념을 모르기에 equivalence relation 을 이용하여 정의를 했었습니다.

오늘은 **equivalence relation**의 개념을 알아보고 ℤ/*n*ℤ 의 예시를 들어 설명해 보겠습니다. 그냥 넘어가려니 찝찝해서 결국 강의를 하게 되네요.. 

Equivalence relation을 정의하기에 앞서 **(binary) relation** 을 정의하겠습니다:

## Definition
![ql_16625dd3f51775da833696cc45a4ce5f_l3.png](https://steemitimages.com/DQmVe56WeLvjDViZTJ3dNYf1z8SNTkwWRcDPTqp2DoPq8mu/ql_16625dd3f51775da833696cc45a4ce5f_l3.png)

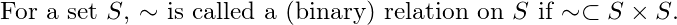
이게 무슨 소리일까요.. 어떤 집합 *S*에 대하여 *S×S*의 부분집합이면 relation 이라고 하네요. 즉 순서쌍들의 집합이라는 거죠.

이해가 안되면 뭐라고 했죠? 예시를 들으라고 했죠.

### Example

*S*=ℝ 이라고 둘게요. (ℝ은 모든실수들의 집합, the set of real numbers)

모두들 잘 아시다시피 우리는 두개의 실수의 **대소비교**를 할 수 있습니다. 예를 들어, 2보다 3이 크고 √3 보다 √5가 크다는건 누구나 알 수 있죠. 이때 부등호 기호를 쓰죠? 부등호 >,<는 초등학생도 알고 있는 **relation** (on ℝ) 입니다. (사실 좀 더 나아가서 order relation on ℝ 입니다)

#### 나올 수 있는 예상 질문:
엥? 그런데 저기 위에 있는 정의를 보면 어떤 집합 *S*에 대하여 *S×S*의 부분집합이면 relation 이라고 했는데, 부등호가 어떤 집합의 부분집합이 될 수 있나요?

### Answer:
네, 될 수 있습니다. 가령 예를 들어, *2*<*3* 이라는 관계가 만족되는 것을 알 수 있죠. 이것을 (*2,3*)∈< 으로 해석 할 수 있죠. 마찬가지로 (√*3*,√*5*)∈< 입니다. 
이렇게 해석을 하면 당연히 <⊂ℝ×ℝ 임을 확인할 수 있습니다.

Relation을 정의하고 잘 이해했으니, 이제 **equivalence relation**을 다음과 같이 정의할 수 있습니다:

## Definition
![ql_6753de6dbac06d6ecaaf6c3b9593717b_l3.png](https://steemitimages.com/DQmTMGcFLQeP7vBZ1vLmcGh7avNVAFQWSWqa5Na5FSxs9uy/ql_6753de6dbac06d6ecaaf6c3b9593717b_l3.png)

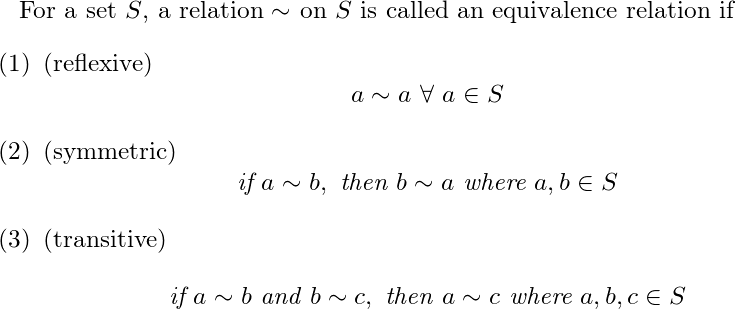
Relation 중에서 Reflexive, Symmetric, Transitive 인 것들을 equivalence relation 이라고 합니다.

> 제가 위에 들었던 예시 부등호 <는 아쉽게도 equivalence relation이 아닙니다. 왜냐하면 *1*<*1* 은 성립하지 않기 때문이죠 (so not reflexive).

>  ≤는 어떨까요? 모든 *r*에 대하여 *r*≤*r* 이 성립하기 때문에 reflexive 입니다. 하지만 *2*≤*3* 이 *3*≤*2* 를 보장하지 않으므로  symmetic 이 아닙니다.

(사실 위의 두 예시는 order relation이 됩니다)

등호 =는 equivalence relation이 됩니다. 구독자 여러분들은 한번 체크해보시기 바랍니다.

### Example
자 그럼 저번 시간에 정의했던 ≡ (mod n) 이 equivalence relation이 되는지 증명해 보겠습니다: (≡ mod n 을 congruence relation, 합동 관계 라고 부릅니다)

> 우선, 정수 *a,b,n* 에 대하여 *a*≡*b* (mod *n*)를 *n*|*a-b* (*n*이 *a-b*를 나눈다) 로 정의했었습니다.
따라서, ≡ (mod n)은 ℤ 위에서 relation이 됩니다.

> *n*|*0*, *0*=*a-a* 이므로 모든 *a*에 대하여 *a*≡*a* (mod *n*)이 성립하여 Reflexive 입니다.

> 만약 정수 *a*,*b*에 대하여 *a*≡*b* (mod *n*) 이면 *n*|*a-b* 이고 *a-b*=*b-a* 이므로 *n*|*b-a*가 되어
*b*≡*a* (mod *n*)  가 됩니다. (Symmetric)

> 정수 *a*,*b*,*c*에 대하여 *a*≡*b* (mod *n*), *b*≡*c* (mod *n*) 이면 *a*-*b*=*nk*, *b*-*c*=*nl*  for some integers *k*,*l* 이고, 따라서  *a*≡*c* (mod *n*) 입니다. (Transitive)

따라서 증명이 끝납니다.

마지막으로 연습문제 하나를 소개하고 끝내겠습니다. 한번 증명해 보시길 바랍니다.

### Exercise
Let *X* be the set of Cauchy sequence in ℚ, where ℚ: the set of rational numbers.
Define a relation ~ on *X* by 
> {a_n}~{b_n} if lim a_n=lim b_n

Show that ~ is an equivalence relation on *X*.

다음 시간에는 집합 *S*를 equivance relation on S 로 자른다(**quotient**)는 개념을 배우겠습니다. 

감사합니다.

## 이미지를 제외한 이 글의 모든 저작권은 @kjs105 에게 있습니다. 이미지는 quicklatex.com 에서 직접 코드를 입력하여 render 하였습니다. 무단 전재 및 배포를 금합니다.