If I start writing down the numbers
<center>
1, 1, 2, 3, 5,  8, 13, 21 ...
</center>
you will probably instantly recognize them as Fibonacci numbers. A quick reminder,  adding any two adjacent numbers generates the next Fibonacci number. So since 1+1 =2  we get that 2 is Fibonacci number, then 1+2=3 so we get that 3 is a Fibonacci numbers.

You probably already read about the connection between the Fibonacci numbers and the golden ratio. However, there are plenty more interesting properties. Today we will look at a `Mathemagical' statement which you can use to read someone's mind :o)


<center>
![381px-Mind-reading-Russell-Morgan.jpeg](https://steemitimages.com/DQmRZM2iN8FfCTbgf2mY2qW6ynaG8r7oPhuaWwLxaBUnpqx/381px-Mind-reading-Russell-Morgan.jpeg)
</center>





# Mathemagic of Fibonacci numbers

Let me start with the `Magical'  statement:

**Mathemagical statement** *Take any two different Fibonacci numbers (they do not have to be adjacent Fibonacci numbers) and then add them together.  Let's call this number X. Suppose you would only tell me X then without knowing which Fibonacci numbers you chose I can determine the Fibonacci numbers you used to get X.* 

To convince you a bit let's first show this with an example. So suppose you are only allowed to use Fibonacci numbers les or equal to 5. Then let's look at all the possibilities

<center>
1+1=2
1+2=3
1+3=4
2+3=5
1+5=6
2+5=7
3+5=8
</center>

You see that for any any whole number between 1 and 9 there is a unique pair of Fibonacci numbers.  You might then think that the following is true: any number greater than one can be written as a unique combination of two different Fibonacci numbers. But this is **not true**. For example, 12 cannot be expressed as the sum of two Fibonacci numbers. 

# Proof by contradiction

 So how do we go about proving this Mathemagical statement. We will prove the Mathemagical statement by using proof by contradiction. This means that will assume that the contrary  of the Mathemagical statement is true and then show that this implies that something which we know should be true is not true.  Let us clarify this with an example: suppose you want to prove that a needle is sharp. Then if you would apply a proof by contradiction you would assume that it is not sharp. So if the needle is not sharp then if I use it to poke my finger then no blood should come out. However, when I used it to poke my finger a fair amount of blood came out. So the initial assumption that the needle is not sharp is incorrect and we conclude that the needle is sharp.  

# Proof of the Mathemagical statement

So how do we formulate the contrary  of the Mathemagical statement? In this setting the contrary means  that the sum of two Fibonacci numbers can be expressend in two (or more) ways. So there  exist four different Fibonacci numbers which we will denote by 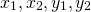![x1x2y1y4](https://steemitimages.com/DQmbn9ciAtk4Aqb9raBoXfULocByHLLAuvguFYrAMcniQbd/ql_9f82429df54831a6c10f174fbd6ad51e_l3.png)  such that

<center>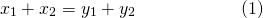![ql_4a3535016849ed0ea07a6d92eacd162c_l3.png](https://steemitimages.com/DQmRacBZJvhuh92ZXTmzR2Np9utkBSZ76PR2JdTaVwcURnh/ql_4a3535016849ed0ea07a6d92eacd162c_l3.png)                             </center>  

One of these Fibonacci numbers 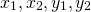![x1x2y1y4](https://steemitimages.com/DQmbn9ciAtk4Aqb9raBoXfULocByHLLAuvguFYrAMcniQbd/ql_9f82429df54831a6c10f174fbd6ad51e_l3.png) has to be the biggest. Without los of generality we can assume that 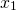![x1](https://steemitimages.com/DQmf5MYdihLf5PRRRYvcnZ2UsXFgbSsYfp763SatpKa4Dgg/ql_7f909dba34eb9e5fbc8395f030896b8e_l3.png) is bigger than the Fibonacci numbers 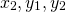 ![ql_9332084f50db513c6cf2d0166d7f674d_l3.png](https://steemitimages.com/DQmZvtASMpNQFDmckijgT9CjKy7TEJB399emnisY5sejFGz/ql_9332084f50db513c6cf2d0166d7f674d_l3.png). We now need to introduce some notation. We will  denote the nth Fibonacci number by 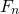 ![Fn](https://steemitimages.com/DQmTpyW8x74w42ra3a2keKQKLggf4RL6dRW2QSa243z1vJx/ql_1151d5e53c2f1b16d3974094ab31f0c3_l3.png). Recalling how Fibonacci numbers are generated we have for 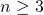![ng3](https://steemitimages.com/DQmPjFsEwfu7YNS8irTwgt3ieGgHt6bmVqYeWoWNtRKCouq/ql_6f22234a615bb07d1f1be7ee1130f5d5_l3.png) that

<center> 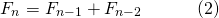 ![ql_23046ce8ad7e1fab6ddc7967e80e2768_l3.png](https://steemitimages.com/DQmVQqJp4Jhia1mPzMHhei5UH6Modxd1PBKExYPFmDf7p7w/ql_23046ce8ad7e1fab6ddc7967e80e2768_l3.png) </center>


We know that that there must exists a k such that 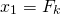 ![ql_97e7ba56d098674f55195cb10aa9be07_l3.png](https://steemitimages.com/DQmVq3WJjyRFkCYy2ddA7BF8AH1w171f7wCgerm8h3bThRB/ql_97e7ba56d098674f55195cb10aa9be07_l3.png). Since all Fibonacci numbers are positive we then get 

<center>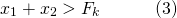![ql_d89816358aeb6fd7dfd2a91f5877d1ac_l3.png](https://steemitimages.com/DQmTyhoLk5sW8w7shjcKoTeS7SVxAtrKzxWwf81d7K1RrF9/ql_d89816358aeb6fd7dfd2a91f5877d1ac_l3.png)
</center>


Since 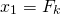![ql_97e7ba56d098674f55195cb10aa9be07_l3.png](https://steemitimages.com/DQmVq3WJjyRFkCYy2ddA7BF8AH1w171f7wCgerm8h3bThRB/ql_97e7ba56d098674f55195cb10aa9be07_l3.png)  is the largest Fibonacci numbers and since ![ql_530df7ecf22669448a0efed609c86f52_l3.png](https://steemitimages.com/DQmSoW1kAVoXBnwPc9GxMMcSSHq1Gzij8YZn3LNAdPXLdM6/ql_530df7ecf22669448a0efed609c86f52_l3.png) are  different Fibonacci numbers we know that 

<center>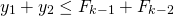![ql_0834e2713b7409b526931bcdfd14ca59_l3.png](https://steemitimages.com/DQmP6FnZ2dj5HUaAzLYHJW9og4F5vac3PmXrpfqAABCUehN/ql_0834e2713b7409b526931bcdfd14ca59_l3.png)</center>

Using (2) we get that
<center> ![ql_4bc4f6879729958e98c7c443a9147eb3_l3.png](https://steemitimages.com/DQmRbcPQ16Z9bmHXLyjTyS7eg5GxhA17xTrkPgzHXu8EceG/ql_4bc4f6879729958e98c7c443a9147eb3_l3.png)</center>

Inserting the inequalities (3) and (4) in the equality (1) we get that

<center>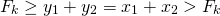![ql_71f00c26e12f65c1b5f47b222db83093_l3.png](https://steemitimages.com/DQmVFUZqtrpBogqxL4E8hYjH26brppu5qjzGwRaRCZ3bi9W/ql_71f00c26e12f65c1b5f47b222db83093_l3.png)</center>

Just to make it a bit clearer let 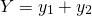![ql_01143b8c4490404059f7d7a3cfa7a9b7_l3.png](https://steemitimages.com/DQmXyyS8Bwk7J1Hy499wbinXSHcdsGgRFyumD1LjzH7YQp8/ql_01143b8c4490404059f7d7a3cfa7a9b7_l3.png). Then we get that

<center>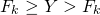![ql_018ac8246dc43725342640bbe3dfe9be_l3.png](https://steemitimages.com/DQmbmGrnXAcMWZ32Cv3mQBwXRKLpmchVWwW28BP7UW6Tu9w/ql_018ac8246dc43725342640bbe3dfe9be_l3.png)</center>

This cannot be true! So have completed the contradiction and in doing so shown the Mathemagical statement. 


# The *little fibs* card trick and the Mathemagical statement

<center>
![Welles-Sandburg-1942.jpg](https://steemitimages.com/DQmanyJupVgTP4KkWbLL19sCxvQqrHxuVK3VdFjzzfKCvez/Welles-Sandburg-1942.jpg)
[Source](https://en.wikipedia.org/wiki/Card_manipulation#/media/File:Welles-Sandburg-1942.jpg)
</center>

This Mathemagical statement has actually been implemented in a card trick, called the *little fibs trick*.  

The magicians shuffles a deck and presents you with a pile of cards. You then selects  two cards. The magician then asks you to add the values of these cards. The values are determines as followd: ace=1, 2=2, 3=3, ..., 10=10, jack=11, queen=12 and king =13 (suits have no value). When you tell the magician the value of the sum  the magician can tell you which cards you selected. 

So how does this trick work? The non-mathematical part is that the magician shuffled the deck in such a way that you could only select from a pile of cards which correspond to Fibonacci numbers. From there on it is just mathematics. So the name of this trick has a double meaning since  *little fibs* means little lie but  it also is a short notation for *little* fibonacci numbers where *little* means low.

Here is a numberphile  [video](https://www.youtube.com/watch?v=4izjrtR8Ozg) showing/explaining the procedure in detail and a bit of the maths. 


# Zeckendorf's theorem

Our Mathemagical statement gives rise to the question under what conditions can any positive whole number be represented as the sum of Fibonacci numbers. The Zeckendorf's theorem answers this question. It states that every positive whole number can be uniquely represented as a Fibonacci number or as the sum of different Fibonacci numbers which do not include consecutive Fibonacci numbers.  So we have the following informal statement 
<center>
*in a very specific sense the Fibonacci numbers form the unique building blocks of the whole numbers*.
</center>
<hr>

## Sources 

This is a bit based on the [numberphile video](https://www.youtube.com/watch?v=4izjrtR8Ozg) about  *the little fibs* magic trick. The proof does not appear in this video. However, somebody put a proof in the comments section of the numberphile video. That proof uses a mathematical technique called induction. This is not necessary. So I think my proof is shorter and easier.

Equations made using [quicklatex](http://quicklatex.com/). It is free to use.

Top picture: [Marvelous feats in mind reading, Litography,  U.S. Printing Co., Russell-Morgan Print (1900), Cincinnati & New York](https://commons.wikimedia.org/wiki/File:Mind-reading-Russell-Morgan.jpeg)

## Further reading

For a proof of the Zeckdorf theorem you can check this [wiki page](https://en.wikipedia.org/wiki/Zeckendorf's_theorem).


<hr>

# Thank you!

Thanks for being so kind to read my post. You are awesome! Please follow me if you enjoyed it. If you have any questions just post them below and I will answer them. Or if you might have a nice topic you want me to cover also let me know below. In my next post I think I will write about continuous functions.  :o)

<hr>

<center>
## Owl tax



![IMG_20171229_171029.jpg](https://steemitimages.com/DQme1bHPxrd7J6RYfkqpvu8dgE66ZKWYjmg7swAYqeqXhRT/IMG_20171229_171029.jpg)


 A few months ago, I visited London.  I found this amazing taxidermy of a Tawny owl in the British Natural History museum.
</center>