I've wanted to write a post about this for a long time; I haven't because its a complex subject for SteemIt, it involves math and won't be very exciting.  But it is about maximizing the odds of increasing your wealth and after some of the comments on one of my recent posts about Andy Hoffman giving up on Gold and gambling by going all-in on Bitcoin [Here](https://steemit.com/steemsilvergold/@matthewwarn/andy-hoffman-gives-up-on-gold), I decided to carve out some time today and post it.  I can feel most of you are giving up already as I type this and that's ok because I've decided I need to review this as well for my own family's benefit.  So today will be a very high level overview of a very complex subject.  

**What Is the Kelly Criterion?**

Basically it is a formula used to determine the optimal size of a series of bets or investments in order to maximize the logarithm of wealth.

<center>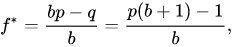![](https://steemitimages.com/DQmNtmMrcaVJpY1c6QLKG9n623tDLxQQy8mU2jFFw9JAoRJ/image.png)</center>

- f * is equal to the fraction of your current bankroll or account to wager
- b is the net odds received on the wager ("b to 1"); that is, you could win $b (on top of getting back your initial bet or investment) 
- p is the probability of winning
- q is the probability of losing (just 1 − p)

It was described by [J. L. Kelly, Jr](https://en.wikipedia.org/wiki/John_Larry_Kelly_Jr.), a researcher at Bell Labs, in 1956.  

<center>![JohnLKellyJr.png](https://steemitimages.com/DQmW8M8MTmmwTioe9VNJDckCRKJEnqyN6k46fy67FKExyzd/JohnLKellyJr.png)</center>

<center>[Source](https://en.wikipedia.org/wiki/John_Larry_Kelly_Jr.)</center>

If you want to simplify the process or just don't care about the math, there are several tools available to do the math for you simply by searching in Google.  I have an excel spreadsheet that I wrote for myself and that I use but I found one online [Here](http://www.albionresearch.com/kelly/).

**Some History**

John Kelly, who worked for Bell Labs, originally developed the Kelly Criterion to assist AT&T with its long distance telephone signal noise problems.  The method was quickly published as ["A New Interpretation Of Information Rate"](http://www.turtletrader.com/kelly.pdf) (1956). However, he also knew of the potential for the method to be applied to other disciplines and once the gambling community got wind of it, they realized its potential as an optimal betting system in horse racing. It enabled pony gamblers to maximize the size of their bankroll over the long term (which is easier said than done). Today, many people use it as a general money management system for not only gambling but also investing in the stock market and recently I personally have been applying it to Cryptocurrencies.  [Warren Buffett](https://seekingalpha.com/article/3411266-warren-buffett-and-the-art-of-focus-investing), [Bill Gross](https://seekingalpha.com/article/69579-edward-thorp-and-bill-gross-how-to-play-your-cards-in-todays-market) & [Ed Thorpe](http://www.valueinvestingworld.com/2013/05/ed-thorp-jack-schwager-and-kelly.html) have all be quoted as using the Kelly Criterion in their investing decisions. 

<center>![download.jpg](https://steemitimages.com/DQmVmt4swzKorKHs5dZAYBY5hC65NWJ2eqkWSjrEMNrDTp2/download.jpg)</center>
<center>[Source](http://www.inforrm.com/interesting-benefits-of-betting-on-horse-racing/)</center>

**In Practice**

For example, if a trader loses $100 on their losing trades and gains $100 on their winning trades, and 60 percent of all trades are winning trades, the Kelly criterion indicates an optimal trade size equal to 20 percent 0.60 − 0.40 = 0.20.

As another example, if a trader wins $200 on their winning trades and loses $100 on losing trades, and the probability of winning and losing are both equal to 50 percent, the Kelly criterion indicates an optimal trade size equal to 25 percent of capital: 0.50 − (0.50/2) = 0.25.

It is also important to note that having all of your trades on at once using this method is also a sure fire way to go broke over a long enough period of time.  You can reduce the trade size % to further minimize your downside risk.  However, increasing your trade size will bring the risk of losing all of your money to nearly 100% as you increase your bet or investment size.  

**In The End**

When the odds are heavily in your favor, profit from the opportunity in front of you. Be greedy when others are fearful and be fearful when others are greedy.  No formula or strategy is perfect, but the Kelly Criterion is a good mathematical guidepost.  

Since no investment is a sure thing, going "all-in" on any investment will mathematically guarantee you of losing all of your money over a long enough period of time.  

<center>![download.jpg](https://steemitimages.com/DQmXTmKBhRDp1cmSC7ypVgp2Y7uhHrWnW3xFF33CTvy41yq/download.jpg)</center>

Pros of the Kelly Criterion:

- Tells your right away whether your odds of making a profit are in your favor or not
- Provides a range of upper and lower values for bankroll allocation decisions
- Comparisons across opportunities are possible

Cons:

- The method requires common sense (a problem for many today)
- Garbage in Garbage out (If your assumptions are wrong, the odds will be wrong and you could be taking significantly bad risks)
- Recommendation relies heavily on your accuracy to determine probabilities and outcomes

@matthewwarn

![DQmZr15ypNrceRJ7qxzHY3zkz9GkDYoGvgNhieh79HT8ZDu.png](https://steemitimages.com/DQmSr1TUAu8AMXYHaBEAc9PCdUPzodxBDjqD5icVjKp4YqT/DQmZr15ypNrceRJ7qxzHY3zkz9GkDYoGvgNhieh79HT8ZDu.png)