Conics in Polar Coordinates: Unified Theorem for Conic Sections
steemstem·@mes·
0.000 HBDConics in Polar Coordinates: Unified Theorem for Conic Sections
https://youtu.be/eUvzyxCfJCw In this video I go over further into Conic Sections and this time go over a more “Unified” theorem for conics that has the benefit of being written down as a simple formula in Polar Coordinates. From my earlier videos on Conic Sections, I went over the conventional theorems for defining Parabolas, Ellipses, and Hyperbolas; which were defined in Cartesian or Rectangular Coordinates. But the issue with the conventional theorems is that Parabolas were defined with a Focus and a Directrix, while Ellipses and Hyperbolas were defined as having two Foci. A more unified approach is to use just one theorem that encompasses all of the conic sections. I go over a summary of such a theorem and which just involves a Focus and a Directrix. The Theorem states that the ratio of the distance from a point to the Focus divided by the distance from the point to the Directrix is equal to e and is called the Eccentricity. When e = 1 the conic is a parabola; when e > 1 the conic is a Hyperbola; and when e < 1 the conic is an ellipse. In this video I go just over a summary of this theorem but in later videos I will go over the proof to show that this does in fact represent conic sections as typically defined in my earlier videos. I also show that this more Unified Theorem has the benefit that when the focus is placed at the origin (or Pole), then this theorem can be written in a short and simple equation in Polar Coordinates. Depending on where the Directrix is, the formula will be slightly modified; which I will explain in more detail in a later video so stay tuned for that as well! This is a great video in both revisiting conic sections but also in explaining how sometimes we can produce more efficient theorems when changing up the coordinate system, so make sure to watch this video! --- Watch Video On: - 3Speak: [https://3speak.tv/watch?v=mes/rgqddsxj](https://3speak.tv/watch?v=mes/rgqddsxj) - Odysee: [https://odysee.com/@mes:8/conics-in-polar-coordinates-unified:2](https://odysee.com/@mes:8/conics-in-polar-coordinates-unified:2) - BitChute: [https://www.bitchute.com/video/eUvzyxCfJCw/](https://www.bitchute.com/video/eUvzyxCfJCw/) - Rumble: [https://rumble.com/v2assuo-conics-in-polar-coordinates-unified-theorem-for-conic-sections.html](https://rumble.com/v2assuo-conics-in-polar-coordinates-unified-theorem-for-conic-sections.html) - DTube: [https://d.tube/#!/v/mes/y5nlpi8i](https://d.tube/#!/v/mes/y5nlpi8i) - YouTube: [https://youtu.be/eUvzyxCfJCw](https://youtu.be/eUvzyxCfJCw) Download PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIh5lCPTNTcPRSp-JVdw --- # View Video Notes Below! --- >Download these notes: Link is in video description. >View these notes as an article: https://peakd.com/@mes >Subscribe via email: http://mes.fm/subscribe >Donate! :) https://mes.fm/donate > >Reuse of my videos: >- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video. > >Fight back against censorship: >- Bookmark sites/channels/accounts and check periodically >- Remember to always archive website pages in case they get deleted/changed. > >Join my private Discord chat room: https://mes.fm/chatroom > >Check out my Reddit and Voat math forums: >- Reddit: https://reddit.com/r/AMAZINGMathStuff >- Voat: https://voat.co/v/AMAZINGMathStuff > >Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook >Follow along my epic video series: >- #MESScience: https://mes.fm/science-playlist >- #MESExperiments: https://peakd.com/mesexperiments/@mes/list >- #AntiGravity: https://peakd.com/antigravity/@mes/series >-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept! >- #FreeEnergy: https://mes.fm/freeenergy-playlist > >--- > >NOTE #1: If you don't have time to watch this whole video: > >- Skip to the end for Summary and Conclusions (if available) >- Play this video at a faster speed. >-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed) >-- Try 4X+ speed by browser extensions or modifying source code. >-- **Browser extension recommendation: https://mes.fm/videospeed-extension** >-- See my tutorial to learn more: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website >- Download and read video notes. >- Read notes on the Hive blockchain #Hive >- Watch the video in parts. > >NOTE #2: If video volume is too low at any part of the video: > >- Download this browser extension recommendation: https://mes.fm/volume-extension --- # Conic Sections in Polar Coordinates 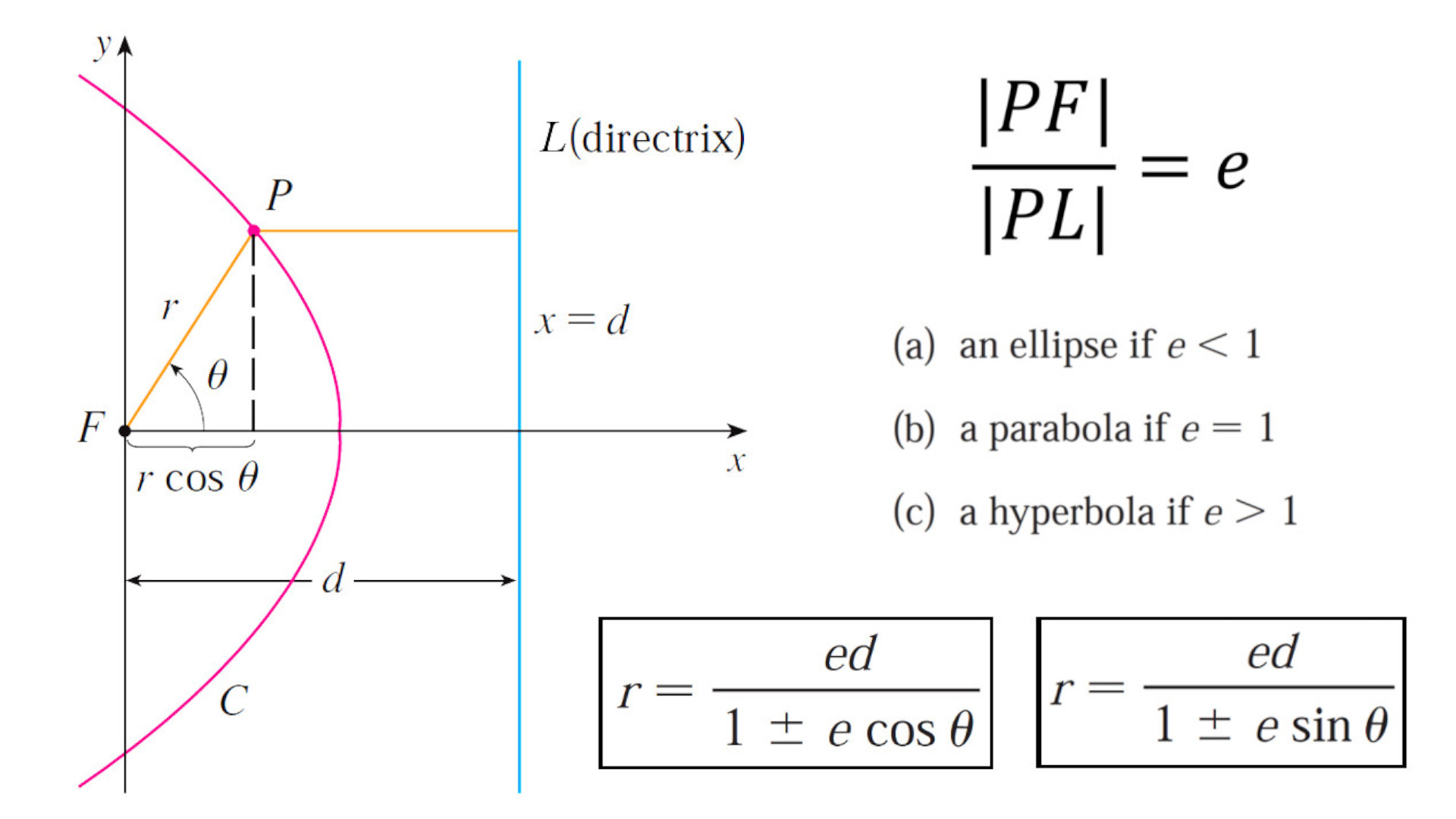 Recall that parabolas, ellipses, and hyperbolas are called conic sections because they result from intersecting a cone with a plane as shown below: 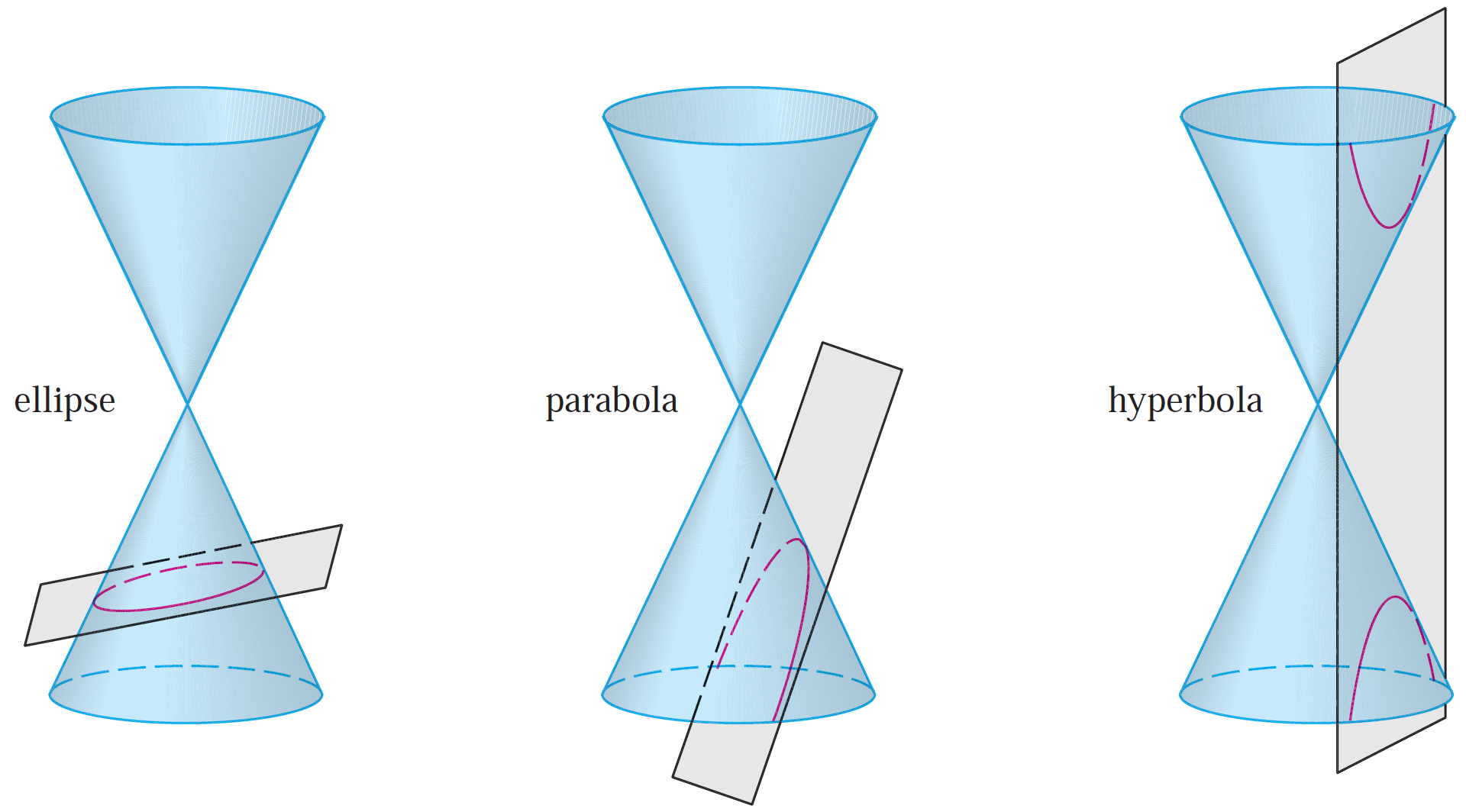 Also recall from my earlier videos that we defined the parabola in terms of a focus and directrix, but instead defined the ellipse and hyperbola in terms of two foci. Parabola: The distance to the foci and to a straight line (the Directrix) are Equal. 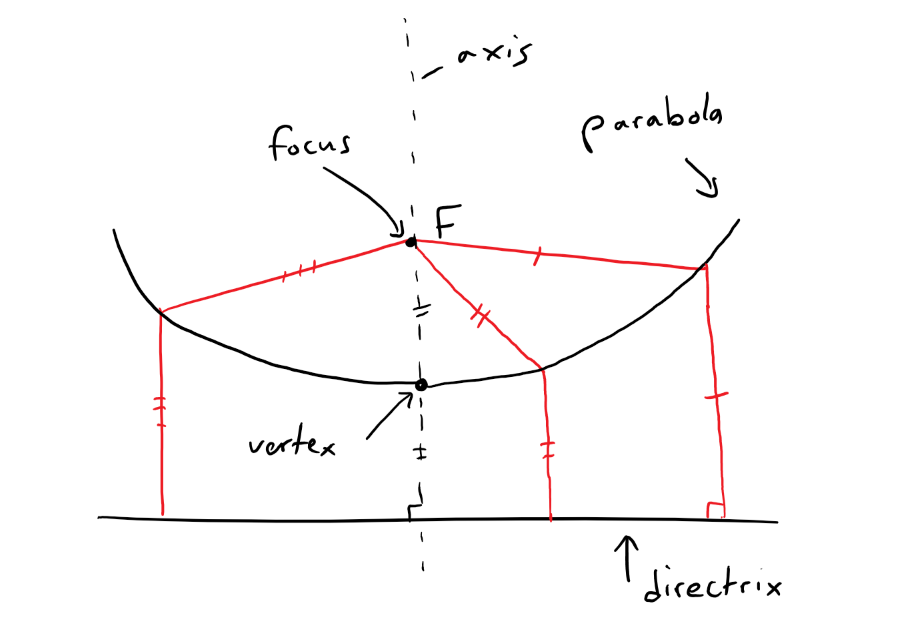 Ellipse: The Sum of the Distances to the Two Foci are Constant. 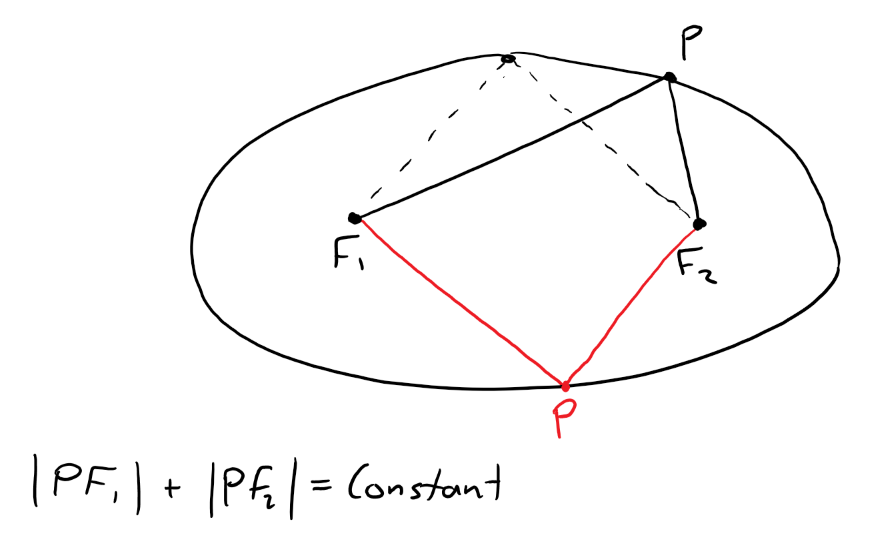 Hyperbola: The Difference of the Distances to the Two Foci are Constant. 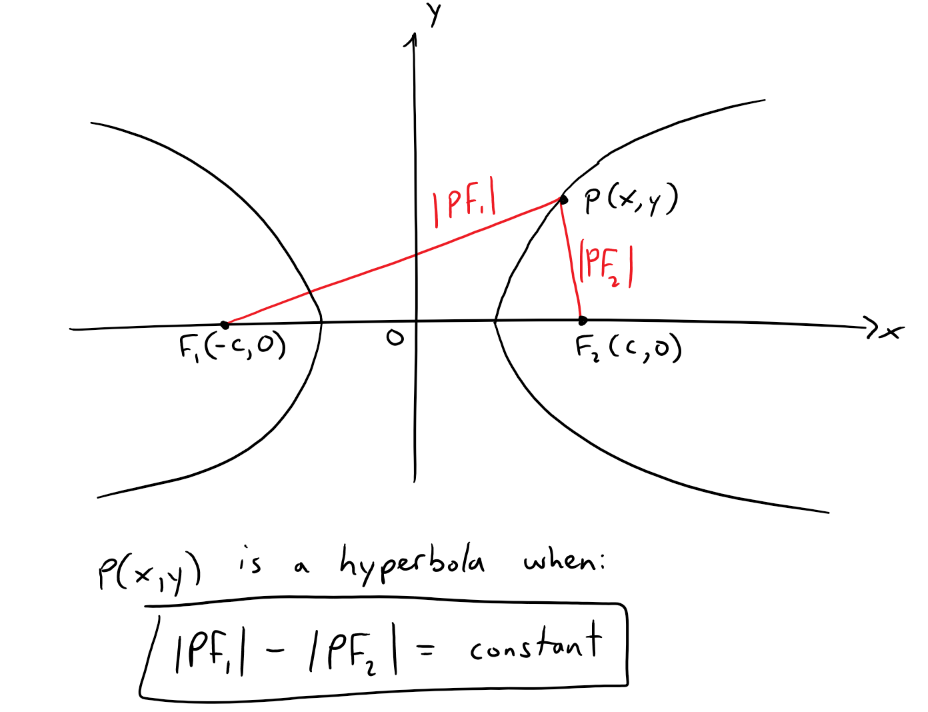 But in this video I explain a more unified treatment of all three types of conic sections in terms of A focus and directrix. Furthermore, if we place the focus at the origin, then a conic section has a simple polar equation, which provides a convenient description of the motion of planets, satellites, and comets. ## THEOREM: Let F be a fixed point (called the focus) and L be a fixed line (called the directrix) in a plane. Let e be a fixed positive number (called the eccentricity). The set of all points P in the plane such that: 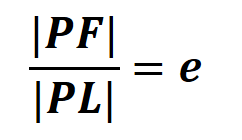 (that is, the ratio of the distance from F to the distance from L is the constant e) is a conic section. The conic is: a) An ellipse if e < 1. b) A parabola if e = 1. c) A hyperbola if e > 1. **MES Note:** -- The eccentricity e is always positive since it is just the ratio of the distances. -- I will prove this theorem in a later video(s) so stay tuned! The Theorem is illustrated below: 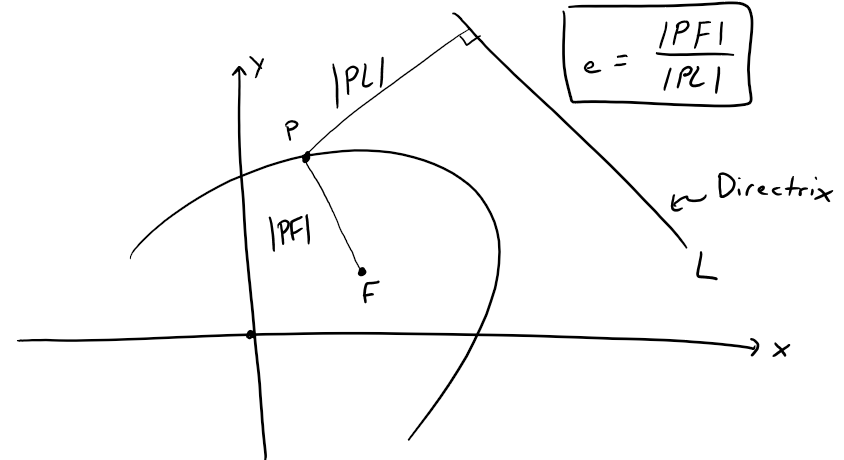 ## THEOREM in Terms of a Simple Polar Equation: A polar equation of the form: 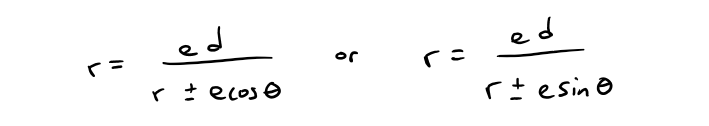 represents a conic section with eccentricity e and the Focus at the origin. The conic is an ellipse if e < 1, a parabola if e = 1, or a hyperbola if e > 1. **The following figures illustrate the different polar equations for various conics:** 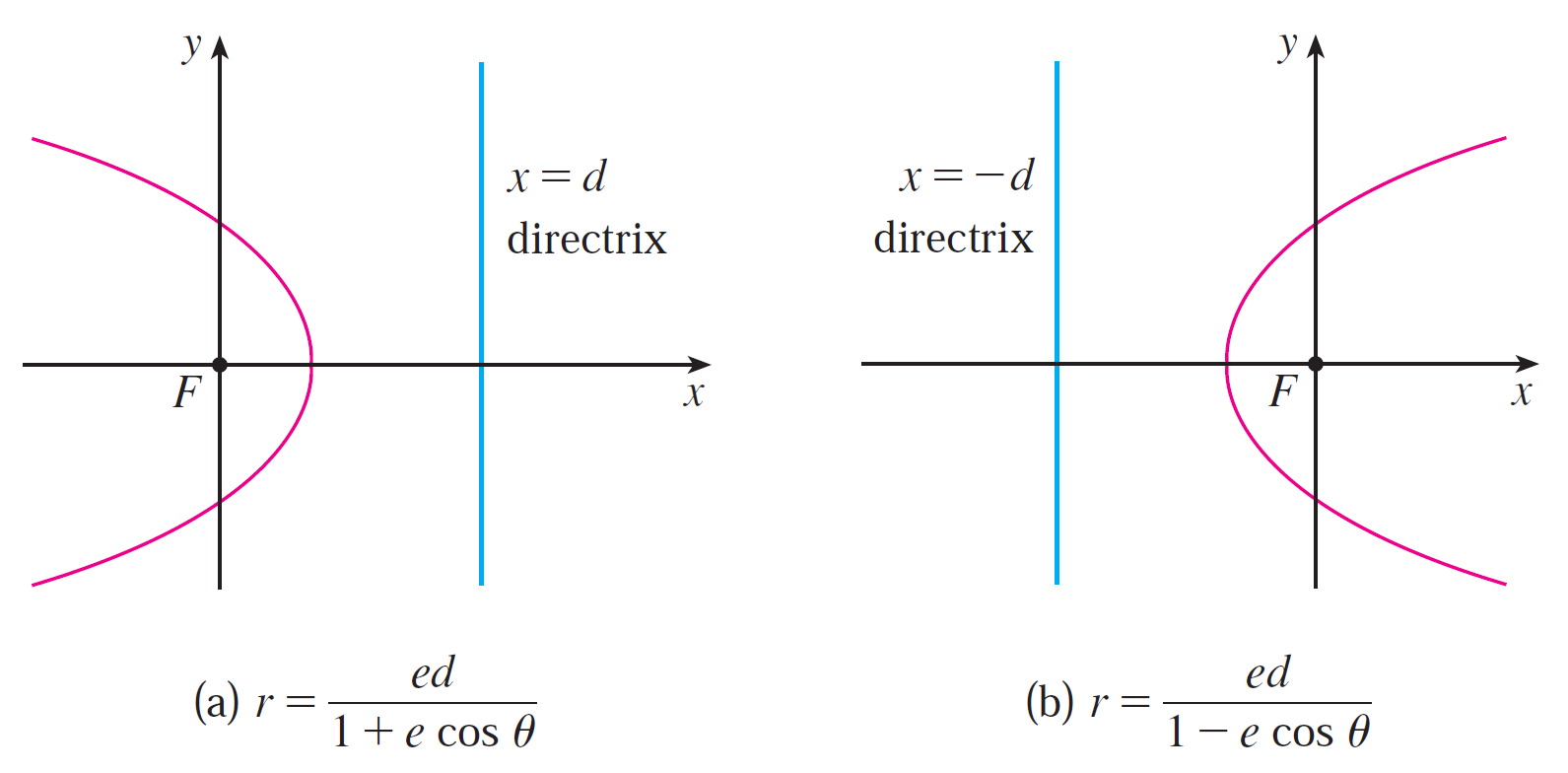 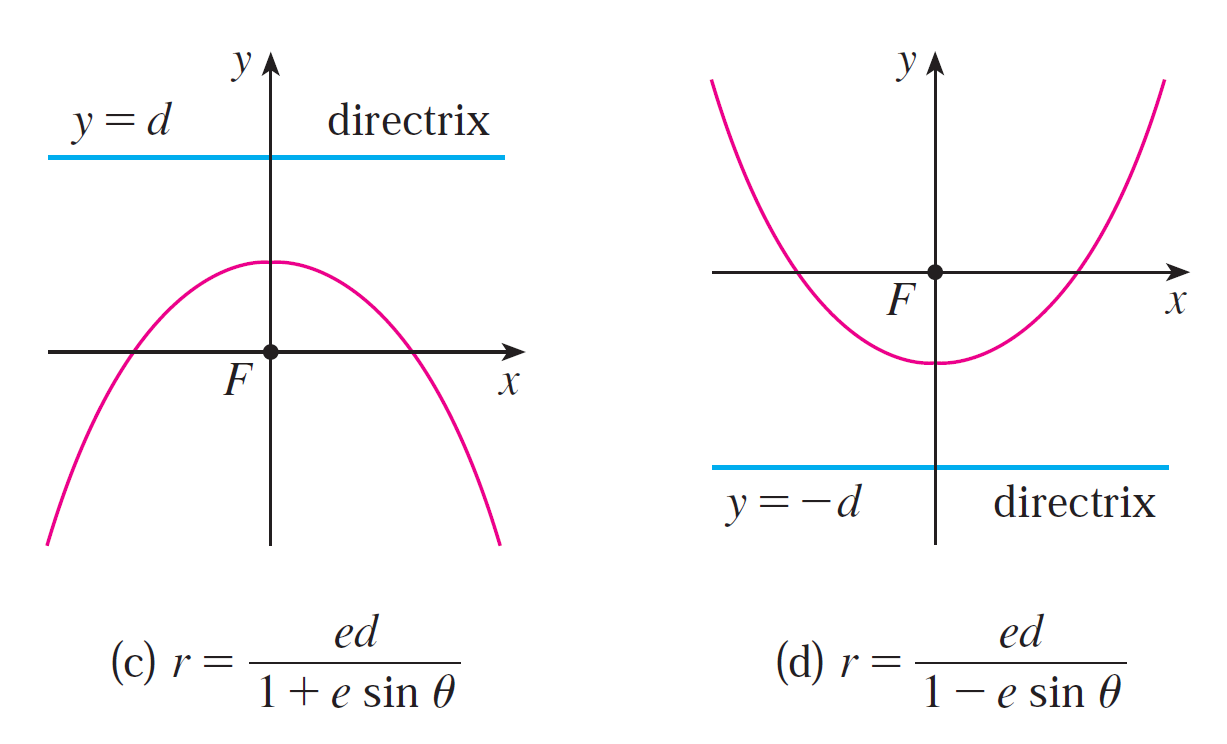 **MES Note:** I will also expand on the different variations of the polar equations for conics in a separate video so stay tuned! Last but not least, recall the connection between Polar Coordinates and Cartesian or Rectangular Coordinates: 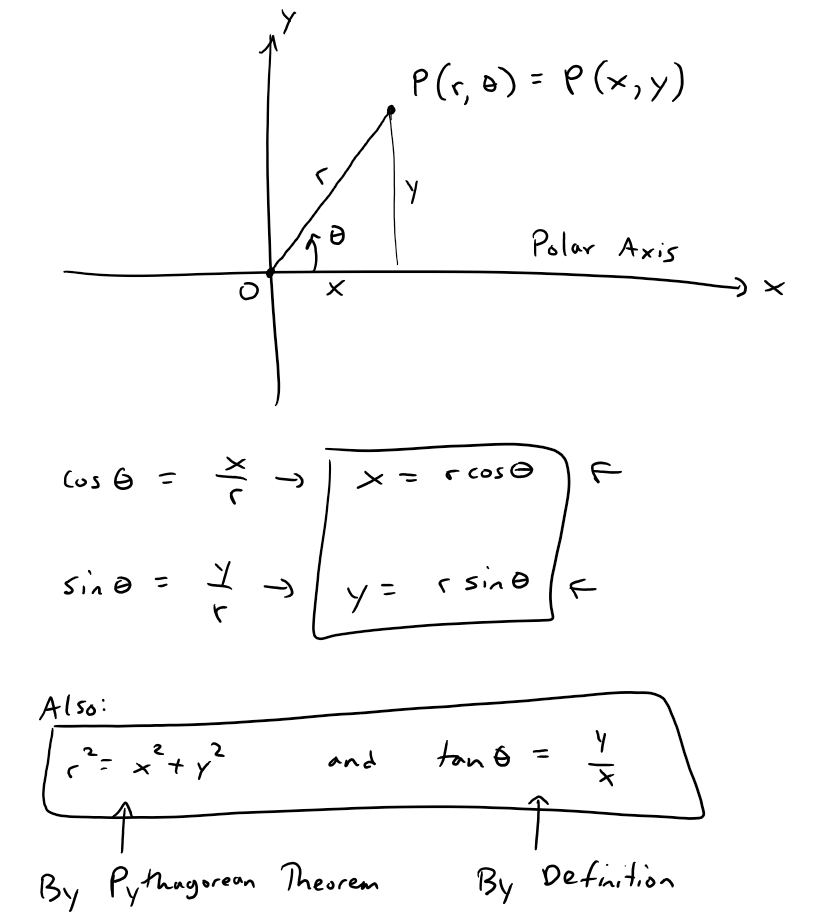 Note: These equations are valid for all angles, and in fact are the general definitions of sine and cosine. For example, if we had an obtuse angle (between p/2 and p radians or 90° and 180°), the relation between Cartesian and Polar coordinates remains the same. 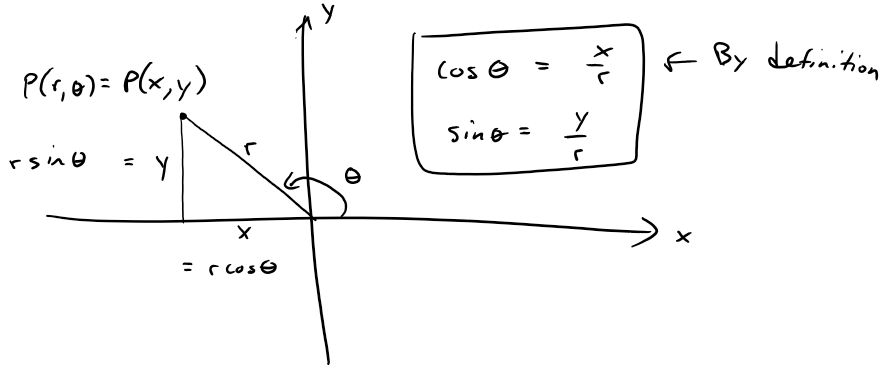 The only difference here is that the cosine function is negative for obtuse angles, and hence the x-coordinate will be negative. 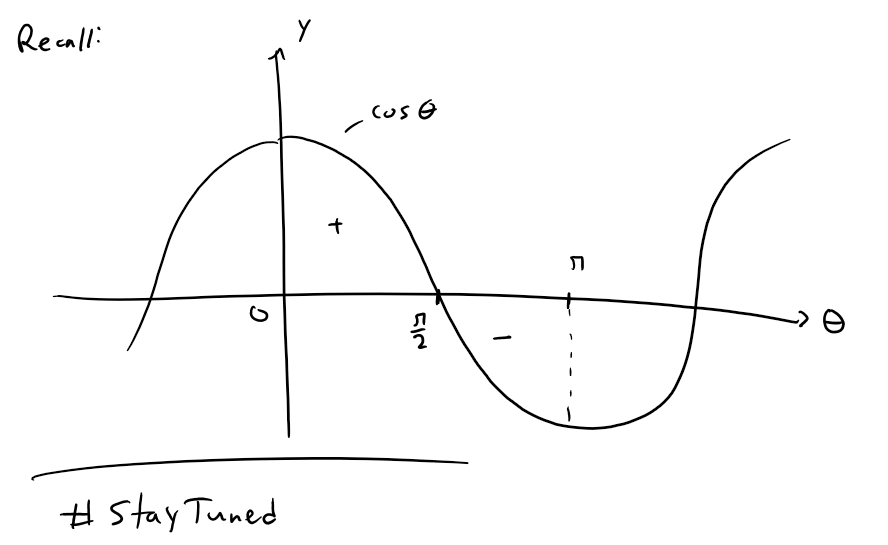
👍 mes, benie111, arslanmustafa, titusfrost, agar, cmp2020, astronomyizfun, cub1, dahbou, itsok, mathiew, trumpman, steemstem, lafona-miner, kryzsec, amavi, dber, gentleshaid, hadji, fredrikaa, abigail-dantes, dysfunctional, leczy, altherion, ertwro, juanjdiaz89, jamhuery, dna-replication, bogh, steemstem-bot, alexander.alexis, ovij, jagsarathore, stemd, voter,