Differential Equations: Population Growth: Logistic Equation: Example 1 (Notes)
mathematics·@mes·
0.000 HBDDifferential Equations: Population Growth: Logistic Equation: Example 1 (Notes)
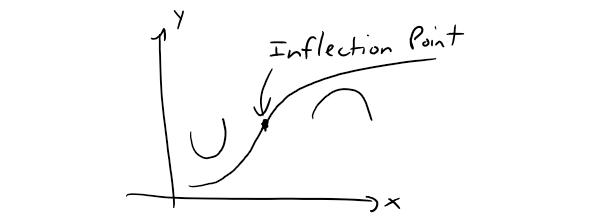
https://youtu.be/FMFTLa8URDg In this video I go over an example on the Logistic Equation for Population Growth and this time analyze a direction field for the equation. The direction field is a good way of seeing how many different solutions to the differential equation behave. The interesting characteristics of the directional field is that the solutions move from the P(t) = 0 equilibrium solution to the P(t) = K (the carrying capacity) equilibrium solution. Also the highest growth rate occurs at half the carrying capacity. The last characteristic I will prove in my next video so stay tuned for that! --- Watch on DTube: https://d.tube/#!/v/mes/tu4500x7 Watch on BitChute: https://www.bitchute.com/video/4DCM0VB4f8K1/ Download PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIhtQpCYjfbY-iusRKGg --- # View Video Notes Below! --- >Download These Notes: Link is in Video Description. >View These Notes as an Article: https://steemit.com/@mes >Subscribe via Email: http://mes.fm/subscribe >Donate! :) https://mes.fm/donate > >Reuse of My Videos: >- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video. > >Fight Back Against Censorship: >- Bookmark sites/channels/accounts and check periodically >- Remember to always archive website pages in case they get deleted/changed. > >Join my private Discord Chat Room: https://mes.fm/chatroom > >Check out my Reddit and Voat Math Forums: >- Reddit: https://reddit.com/r/AMAZINGMathStuff >- Voat: https://voat.co/v/AMAZINGMathStuff > >Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook >Follow My #FreeEnergy Video Series: https://mes.fm/freeenergy-playlist >Watch my #AntiGravity Video Series: https://mes.fm/antigravity-playlist >Follow My #MESExperiments Video Series: https://mes.fm/experiments-playlist> > >--- > >NOTE: If you don't have time to watch this whole video: > >- Skip to the end for Summary and Conclusions (If Available) >- Play this video at a faster speed. >-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed) >-- Try 4X+ Speed by Browser Extensions, HookTube.com, Modifying Source Code. >-- **Browser Extension Recommendation: https://mes.fm/videospeed-extension** >- Download and Read Notes. >- Read notes on Steemit #GetOnSteem >- Watch the video in parts. --- # Example: Draw a direction field for the logistic equation with k = 0.08 and carrying capacity K = 1000. What can you deduce about the solutions? 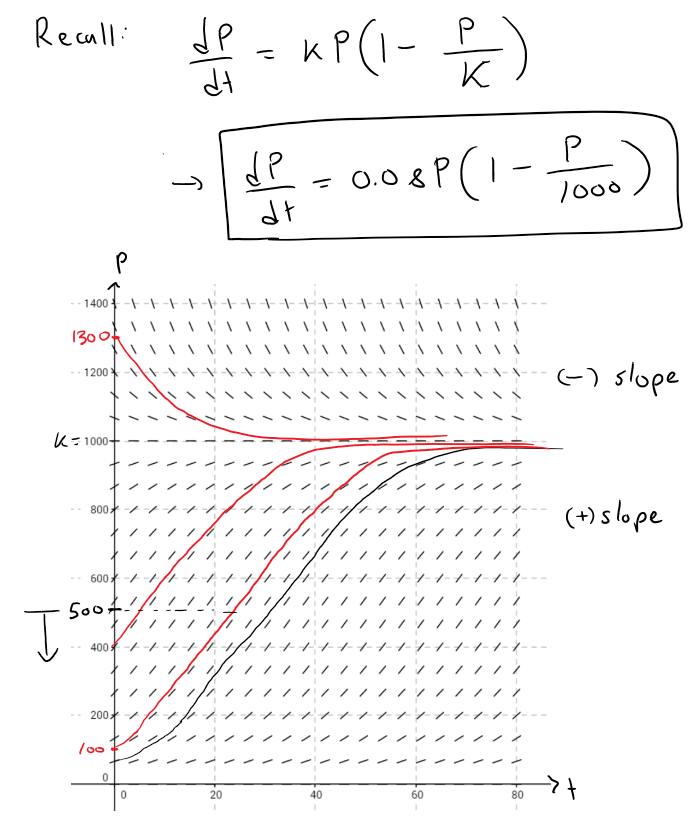 The logistic equation is autonomous (dP/dt depends only on P, not t), so the slopes are the same along the horizontal line. As expected the slopes are positive for 0 < P < 1000 and negative for P > 1000. The slopes are small when P is close to 0 or 1000 (the carrying capacity). Notice that the solutions move away from the equilibrium solution P = 0 and move toward the equilibrium solution P = 1000. 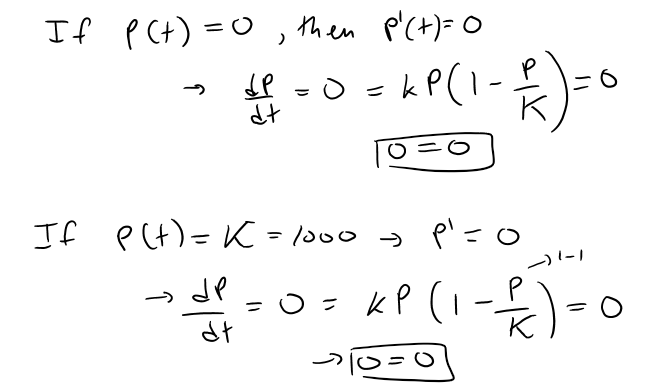 Let's use the direction field to sketch solution curves with initial populations P(0) = 100, 400, and 1300. Notice that solution curve that start below P = 1000 are increasing and those that start above P = 1000 are decreasing. The slopes are greatest when P ≈ 500. - In fact we can prove that all solution curves that start below P = 500 have an inflection point when P is exactly 500. - Recall that an inflection point is when the 2nd derivative changes signs, i.e. changes concavity. - I will go over this in my next video, so stay tuned!