<liketuimages>
<center>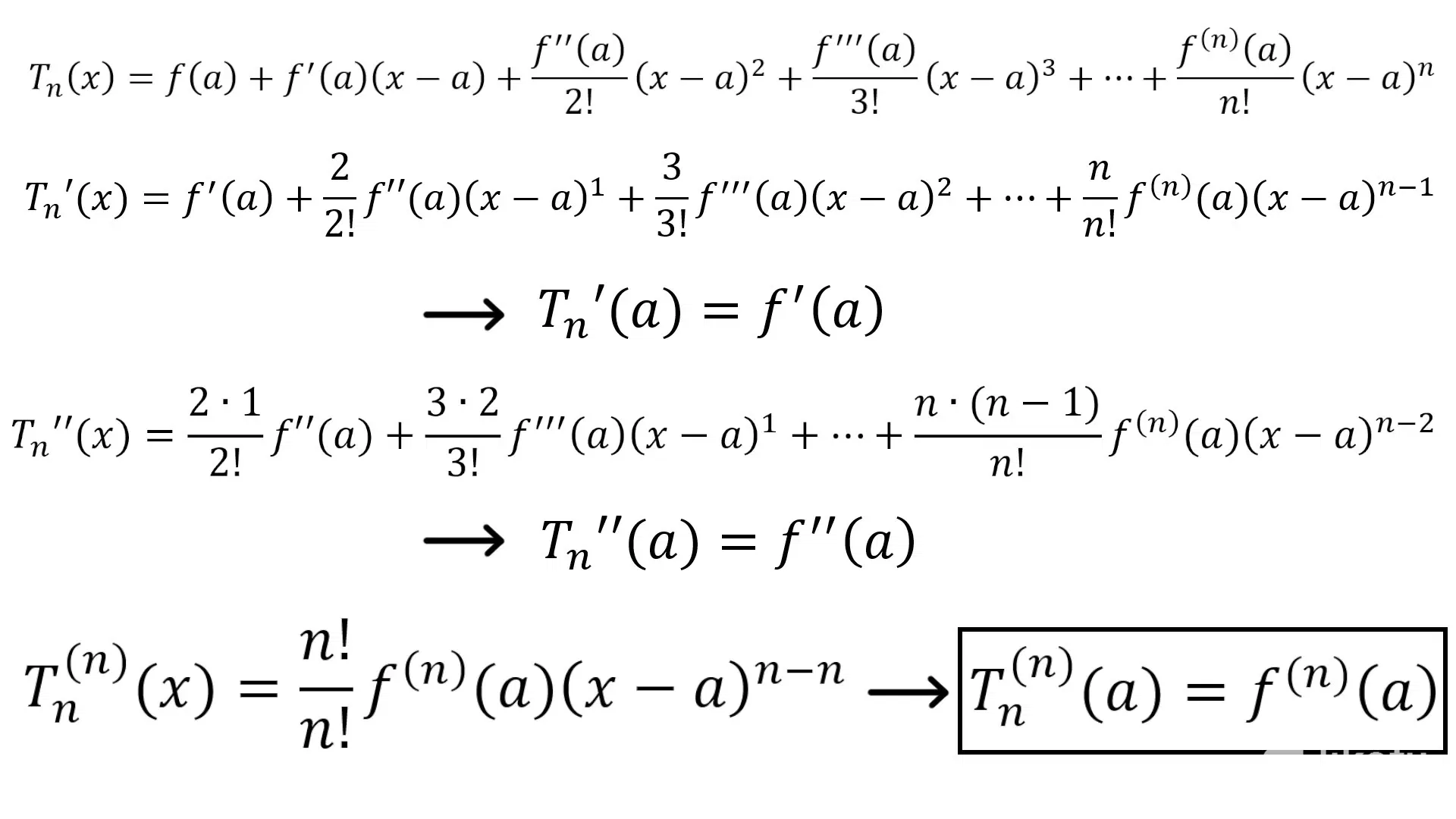
![HN9E9FJXYao82Qnx_7_Exercise_1_Taylor_Derivatives.webp](https://cdn.liketu.com/media/mes/images/HN9E9FJXYao82Qnx_7_Exercise_1_Taylor_Derivatives/HN9E9FJXYao82Qnx_7_Exercise_1_Taylor_Derivatives.webp)
</center>
</liketuimages>

In this video I prove that the derivatives of a Taylor Polynomial are equal to the derivatives of the corresponding function used in the approximation when x = a. This is because any derivative at x = a of any Taylor polynomial cancels out all the terms (since a - a = 0) except the first term, which is just the corresponding derivative of f at x = a. [https://youtu.be/UqWf2PE1OeE](https://youtu.be/UqWf2PE1OeE)

---

For the best experience view this post on [Liketu](https://liketu.com/@mes/exercise-1-taylor-derivatives-equal-the-functions-derivatives-at-x-a)