Laboratory Project: An Elusive Limit
hive-128780·@mes·
0.000 HBDLaboratory Project: An Elusive Limit
https://youtu.be/pwcubhBludE ▶️ [Watch on 3Speak](https://3speak.tv/watch?v=mes/mpbajmmt) - [Odysee](https://odysee.com/@mes:8/laboratory-project-an-elusive-limit:2) - [BitChute](https://www.bitchute.com/video/PLEhi1Tr1GNG/) - [Rumble](https://rumble.com/v1rc6d8-laboratory-project-an-elusive-limit.html) - [YouTube](https://youtu.be/pwcubhBludE) - [PDF notes](https://1drv.ms/b/s!As32ynv0LoaIiL8FaIRCuICnLYyMZg) In this video I go over the Laboratory Project titled An Elusive Limit. Laboratory Projects are interesting math projects at the end of some sections of my calculus book, and in this case at the end of the section on Taylor and Maclaurin Series. The project I cover involves solving the limit of a function that has a difference in the numerator and denominator; and both include trigonometric sine and tangent functions, as we well as inverse trigonometric sine and tangent functions. The interesting part of all of these functions is that as **x** approaches **0**, then they all approach **0** in about the same rate so that their values are near identical to a high level of digits precision. This makes the resulting differences in the numerator and denominator of the function cancel out most of the digits and thus we are left with only a few correct decimal places. This makes the resulting calculations highly dependent on the level of precision of the calculator being used, and in most cases the calculator won’t be able to brute force calculate the function at values very close to **x = 0**. In this case we can still solve the limit in several ways, either by using a computer algebra system (CAS) to solve derivatives or power series of the numerator and denominator, and thus be able to use methods such as l’Hospital’s Rule or other limit laws and algebra manipulation. This effectively means that if we can’t compute the function directly we can instead focus on simplifying or transforming the numerator and denominator into their equivalent but different formulations, which may allow for the limit to be solved through algebraic or calculus means. This is a very interesting tutorial involving the use of calculators and understanding the levels of precision to be certain that the calculations are correct, so make sure to watch this video! The topics covered in this video are listed below with their time stamps. - @ 1:12 - Topics to Cover 1. @ 1:33 - Laboratory Project: An Elusive Limit - 6 Questions 2. Solutions - @ 3:13 - Solution to Question 1 - @ 19:51 - Solution to Question 2 - @ 21:14 - Solution to Question 3 - @ 28:40 - Solution to Question 4 - @ 41:12 - Solution to Question 5 - @ 43:13 - Solution to Question 6 --- ### [Video sections playlist](https://www.youtube.com/playlist?list=PLai3U8-WIK0Gzt0ZAIWwnyZr91b7BGoGR) - [Infinite Sequences and Series playlist](https://www.youtube.com/playlist?list=PLai3U8-WIK0EXHAJ3vRg0T_kKEyPah1Lz) --- # View Video Notes Below! --- >[Become a MES Super Fan](https://www.youtube.com/channel/UCUUBq1GPBvvGNz7dpgO14Ow/join) - [Donate](https://mes.fm/donate) - [Subscribe via email](http://mes.fm/subscribe) - [MES merchandise](https://mes.fm/store ) >- [MES Links webpage](https://mes.fm/links) - [MES Links Telegram](https://t.me/meslinks) - [MES Truth](https://mes.fm/truth) > >**Reuse of my videos:** >- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video. >>**Fight back against censorship:** >- Bookmark sites/channels/accounts and check periodically. >- Remember to always archive website pages in case they get deleted/changed. > >**Recommended Books:** ["Where Did the Towers Go?"](https://mes.fm/judywoodbook) by Dr. Judy Wood > >**Join my forums:** [Hive community](https://peakd.com/c/hive-128780) - [Reddit](https://reddit.com/r/AMAZINGMathStuff) - [Discord](https://mes.fm/chatroom) > >**Follow along my epic video series:** [MES Science](https://mes.fm/science-playlist) - [MES Experiments](https://peakd.com/mesexperiments/@mes/list) - [Anti-Gravity](https://peakd.com/antigravity/@mes/series) ([MES Duality](https://peakd.com/antigravity/@mes/antigravity-part-6-video-1-objects-in-rotation-defy-mainstream-physics-mes-duality-concept)) - [Free Energy](https://mes.fm/freeenergy-playlist) - [PG](https://peakd.com/pg/@mes/videos) > >--- > >**NOTE 1:** If you don't have time to watch this whole video: > >- Skip to the end for Summary and Conclusions (if available) >- Play this video at a faster speed. >-- TOP SECRET LIFE HACK: Your brain gets used to faster speed! >-- [MES tutorial](https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website) >- Download and read video notes. >- Read notes on the Hive blockchain $HIVE >- Watch the video in parts. >-- Timestamps of all parts are in the description. > >**Browser extension recommendations:** [Increase video speed](https://mes.fm/videospeed-extension) - [Increase video audio](https://mes.fm/volume-extension) - [Text to speech](https://mes.fm/speech-extension) ([Android app](https://mes.fm/speech-android)) – [Archive webpages](https://chrome.google.com/webstore/detail/archive-page/gcaimhkfmliahedmeklebabdgagipbia) --- # Laboratory Project: An Elusive Limit  ## Calculus Book Reference Note that I mainly follow along the following calculus book: >**Calculus: Early Transcendentals Sixth Edition by James Stewart** Note that "Laboratory Projects" are interesting math projects at the end of several sections in my calculus book, and in this case it is at the end of the section on Taylor and Maclaurin Series. --- ## Topics to Cover 1. Laboratory Project: An Elusive Limit - 6 Questions 2. Solutions - Solution to Question 1 - Solution to Question 2 - Solution to Question 3 - Solution to Question 4 - Solution to Question 5 - Solution to Question 6 --- # Laboratory Project: An Elusive Limit This project deals with the function:  ## Question 1 Use your **computer algebra system (CAS)** to evaluate **f(x)** for **x = 1**, **0.1**, **0.01**, **0.001**, and **0.0001**. Does it appear that **f** has a limit as **x → 0**? ## Question 2 Use the CAS to graph **f** near **x = 0**. Does it appear that **f** has a limit as **x → 0**? ## Question 3 Try to evaluate **lim<sub>x→0</sub> f(x)** with l'Hospital's Rule, using the CAS to find derivatives of the numerator and denominator. What do you discover? How many applications of l'Hospital's Rule are required? ## Question 4 Evaluate **lim<sub>x→0</sub> f(x)** by using the CAS to find sufficiently many terms in the Taylor series of the numerator and denominator. Use the command **"taylor"** in Maple or **"Series"** in mathematica. ## Question 5 Use the limit command on your CAS to find **lim<sub>x→0</sub> f(x)** directly. Most computer algebra systems use the method of **Question 4** to computer to compute limits. ## Question 6 In view of the answers to **Questions 4** and **5**, how do you explain the results in **Questions 1** and **2**? --- ## Solution to Question 1 The Calculus book solutions manual states it used the Maple mathematics or CAS software program, which has **10** digits of precision, to calculate the following table of values for **f(x)**.  The results of this project will vary depending on the CAS and precision level. In this case, it appears that as **x → 0<sup>+</sup>**, then **f(x) → 10/3**. Note that f is an even function, thus **f(x) → 10/3** as **x → 0<sup>-</sup>** and thus as **x → 0**. We can show that f is an even function, that is **f(-x) = f(x)**, as follows:   When I did the same calculations using Microsoft Excel, I get the following table of values. >https://1drv.ms/x/s!As32ynv0LoaIiL5bYefBaVp2LGff5Q?e=cJkUr1 >Retrieved: 15 October 2020 >Archive: Not available 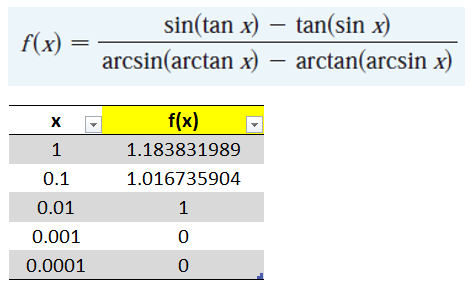 >Note that Excel uses 15 digits of precision. Using the Desmos calculator, we get the following. >[https://www.desmos.com/calculator/vhwpqsail1](https://www.desmos.com/calculator/vhwpqsail1) >Retrieved: 17 October 2020 >Archive: https://archive.vn/wip/IIUpm 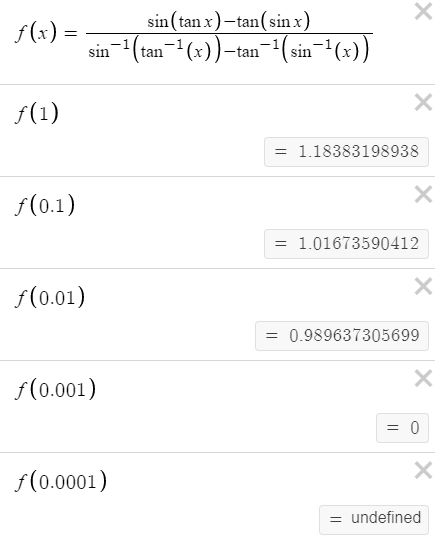 >Note that Desmos uses a dynamic system between **15** and **17*8 digits of precision. We can summarize below the different calculation methods: >Maple, **10** digits of precision: **f(x) → 10/3** as **x → 0**. > >Excel, **15** digits of precision: **f(x) → 0** as **x → 0**. > >Desmos, **15** to **17** digits of precision: **f(x) → undefined** as **x → 0**. Thus, it is not clear if **f** has a limit or not as **x → 0**. --- ## Solution to Question 2 The graph of **f** near **x = 0**, from the solutions manual, is shown below. 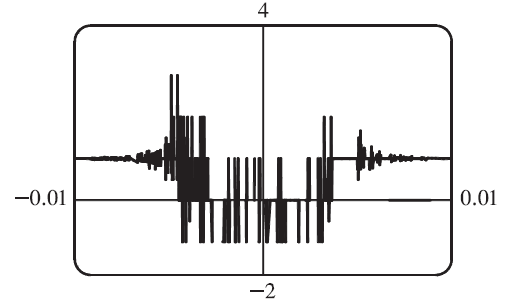 The graph is inconclusive about the limit of **f** as **x → 0**. Likewise, the graph of **f** using the Desmos calculator is also unclear. >[https://www.desmos.com/calculator/vhwpqsail1](https://www.desmos.com/calculator/vhwpqsail1) 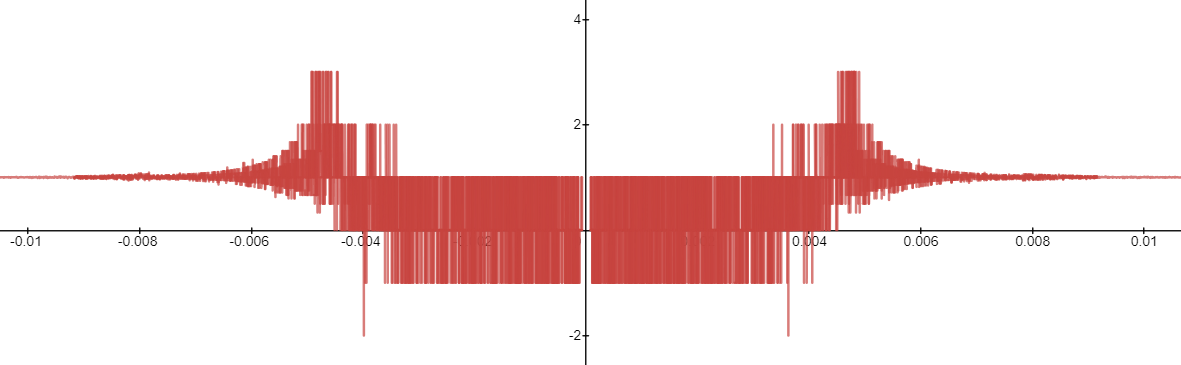 --- ## Solution to Question 3 If we take the limit as **x → 0** we get the indeterminate form **0/0**. 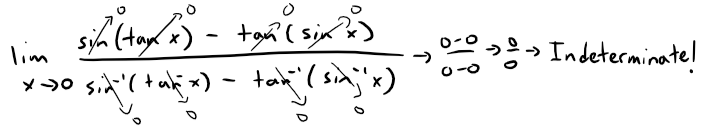 Thus we can apply l'Hospital's rule, referenced from my earlier video. >[https://youtu.be/FhFWfVUBXC4](https://youtu.be/FhFWfVUBXC4) >Retrieved: 3 October 2020 >Video notes archive: https://archive.vn/qiZ5r  Since the Laboratory Project asks us to use a CAS to solved the derivatives of the numerator and denominator, we can use the amazing Wolfram Alpha website. The first **6** derivatives all yield a limit of the indeterminate form **0/0**. Finally, on the seventh application of l'Hospital's Rule we obtain non-zero values! >[https://www.wolframalpha.com/input/?i=7th+derivative+of+sin%28tan+x%29-tan%28sin+x%29+at+x%3D+0](https://www.wolframalpha.com/input/?i=7th+derivative+of+sin%28tan+x%29-tan%28sin+x%29+at+x%3D+0) >Retrieved: 17 October 2020 >Archive: https://archive.vn/wip/fSor5  >[https://www.wolframalpha.com/input/?i=7th+derivative+of+asin%28atan+x%29-atan%28asin+x%29+at+x%3D+0](https://www.wolframalpha.com/input/?i=7th+derivative+of+asin%28atan+x%29-atan%28asin+x%29+at+x%3D+0) >Retrieved: 17 October 2020 >Archive: https://archive.vn/wip/QGgUI 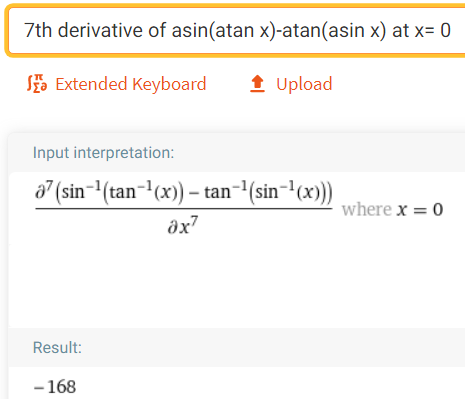 Thus the limit is: 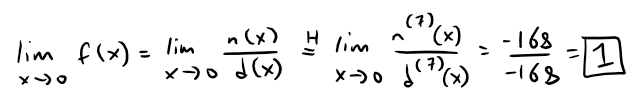 Note that **n(x)** and **d(x)** are the numerator and denominator, respectively, of **f(x)**. --- ## Solution to Question 4 We are now asked to solve the limit using a CAS to determine the Taylor series of the numerator and denominator. Using our trusty Wolfram Alpha calculator, we can determine the Taylor series centered at **x = 0**, i.e. the Maclaurin series, for both the numerator and denominator. >[https://www.wolframalpha.com/input/?i=Taylor+series+of+sin%28tan+x%29+-+tan%28sin+x%29](https://www.wolframalpha.com/input/?i=Taylor+series+of+sin%28tan+x%29+-+tan%28sin+x%29) >Retrieved: 17 October 2020 >Archive: https://archive.vn/wip/E5VUH 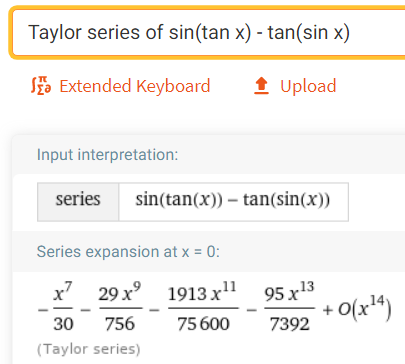 >[https://www.wolframalpha.com/input/?i=Taylor+series+of+asin%28atan+x%29+-+atan%28asin+x%29](https://www.wolframalpha.com/input/?i=Taylor+series+of+asin%28atan+x%29+-+atan%28asin+x%29) >Retrieved: 17 October 2020 >Archive: https://archive.vn/wip/5atb2  Note that the **O** is termed the **"Big O Notation"** and used to indicate that the series has a maximum absolute value beyond the evaluated terms. In our case **O(x<sup>14</sup>)** indicates the series sum of the remaining terms has a maximum value at of a constant multiplied by **|x<sup>14</sup>|** when **x** is close to **0**. >Learn more on here: https://en.wikipedia.org/wiki/Big_O_notation Thus, evaluating the limit of the Taylor series, we have: 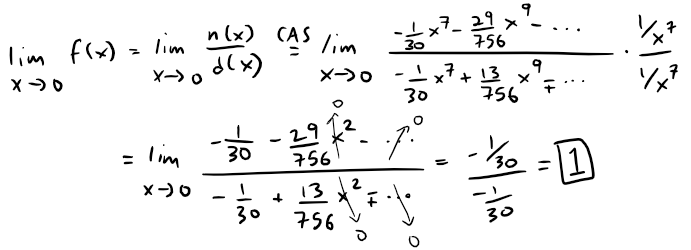 Note that we could've also applied l'Hospital's Rule to the Taylor series **7** times to obtain the same result as **Question 3**. 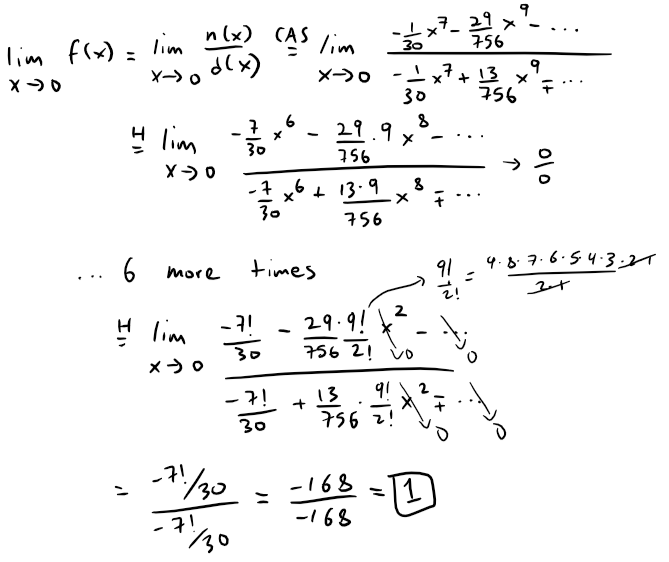 **Calculation check:** >**7! = 5,040** >**-7!/30 = -168** This result agrees with the result in **Question 3**. --- ## Solution to Question 5 If we calculate the limit directly using Wolfram Alpha we get the correct answer. >[https://www.wolframalpha.com/input/?i=limit+of+%28sin%28tan%28x%29%29+-+tan%28sin+x%29%29%2F%28asin%28atan+x%29+-+atan%28asin+x%29%29+as+x+approaches+0](https://www.wolframalpha.com/input/?i=limit+of+%28sin%28tan%28x%29%29+-+tan%28sin+x%29%29%2F%28asin%28atan+x%29+-+atan%28asin+x%29%29+as+x+approaches+0) >Retrieved: 17 October 2020 >Archive: https://archive.vn/18SGs 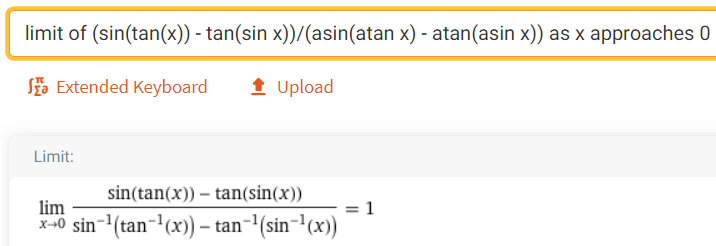 --- ## Solution to Question 6 The strange results (with only **10** to **17** digits of precision) from **Question 1** and **2** must be due to the fact that the terms being subtracted in the numerator and denominator are very close in value when **|x|** is small. Thus, the differences are imprecise (have few correct digits). We can see this is the case by comparing the graphs of the terms in the numerator as well as comparing the terms in the denominator. When we zoom in near **x = 0** we see that the values of the terms are almost identical and to any level of zoom we get to. >[https://www.desmos.com/calculator/vhwpqsail1](https://www.desmos.com/calculator/vhwpqsail1) 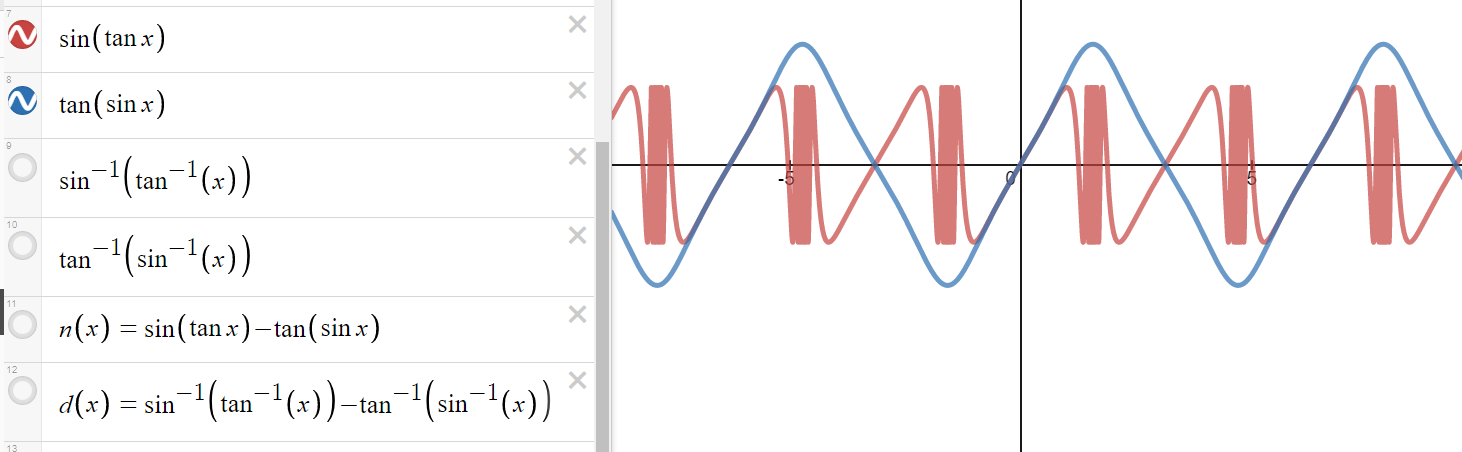  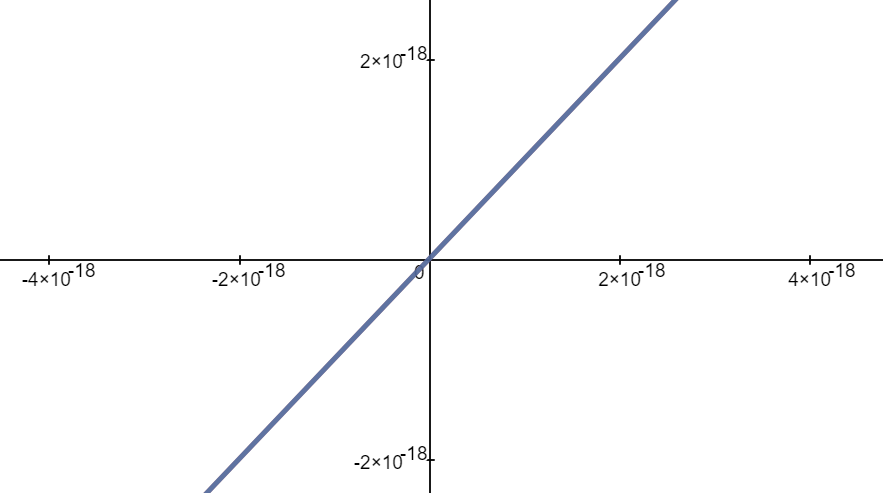 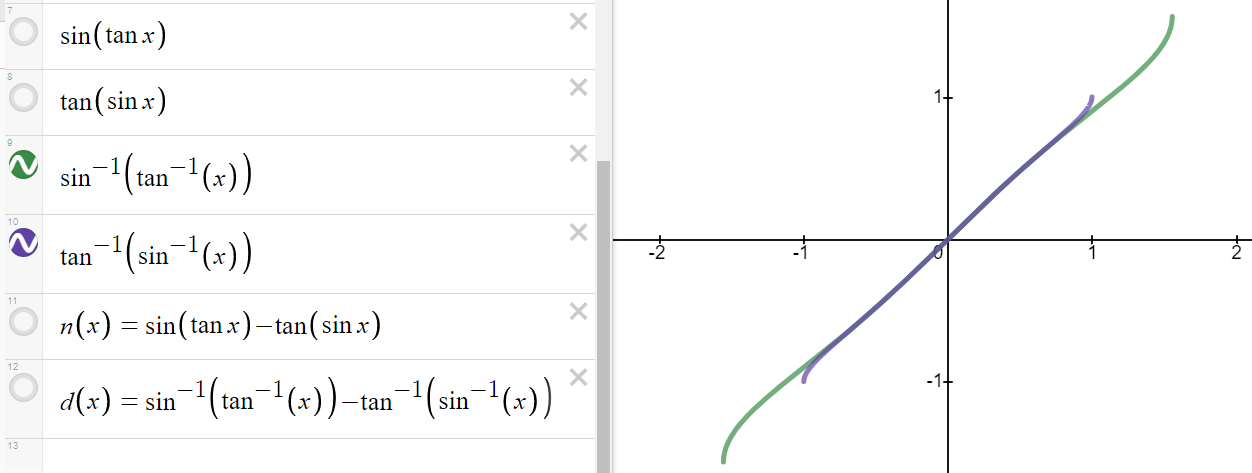 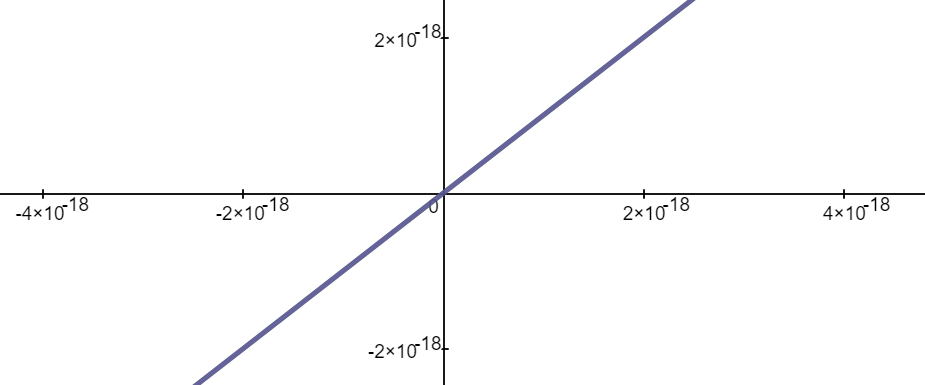 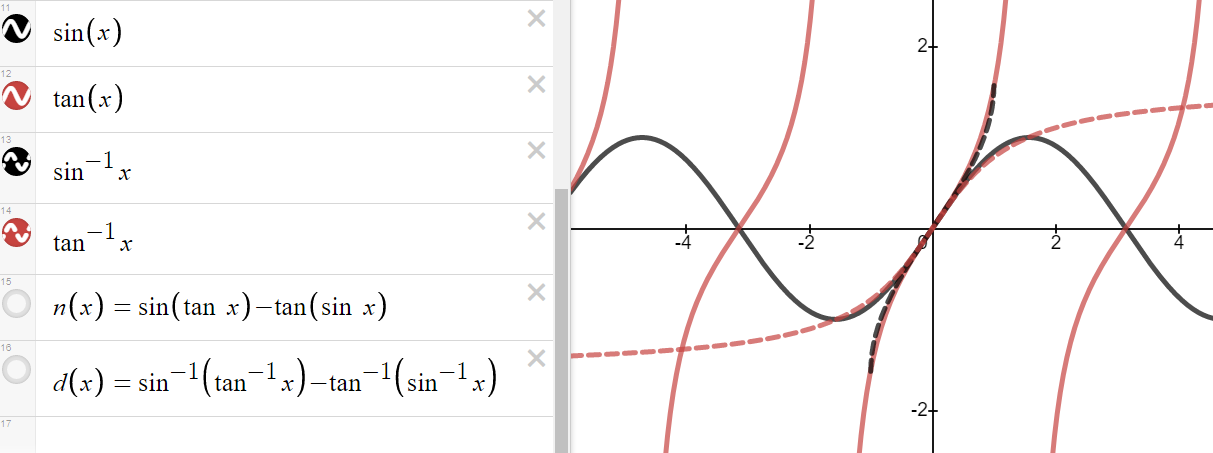 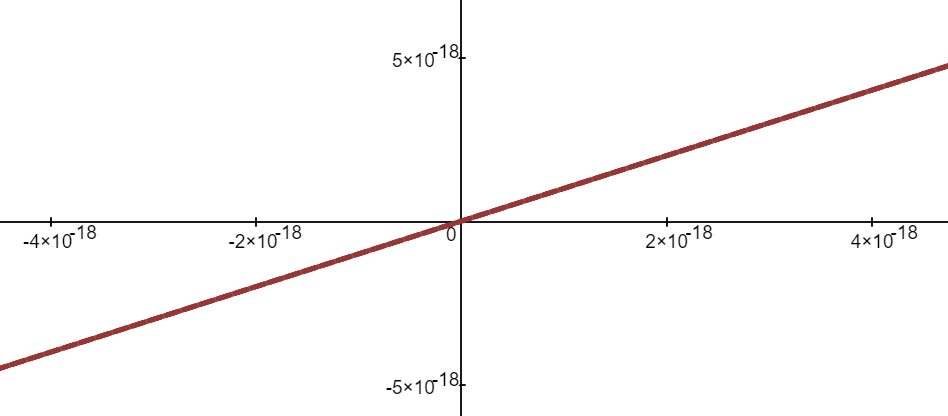 Thus, the terms themselves are near identical when zooming in beyond even the level of precision of most calculators. To illustrate what this means, consider the following calculations of **10** digits of precision: Division: >Exact: > >**0.000012345<u>279</u>** >**÷ 0.000012345<u>111</u>** >**= 1.000013608<u>626</u>** > >Calculator: > >**0.000012345** >**÷ 0.000012345** >**= 1.000000000** Difference: >Exact: > >**0.000012345<u>279</u>** >**- 0.000012345<u>111</u>** >**= 0.000000000<u>168</u>** > >Calculator: > >**0.000012345** >**- 0.000012345** >**= 0.000000000** And dividing differences that are rounded to **0** is undefined, i.e. get the indeterminate form **0/0**. #InterestingStuff
👍 tonimontana, limka, stemcur, jk6276, vxc.stem, mintrawa, kriang3tee, imtase, baiboua, akioexzgamer, french-tech, yuza, paopaoza, ten-years-before, puza, crypto.story, univers.crypto, steementertainer, nalexadre, baneenabear, jesusjacr, alphacore, ripperone, mmmmkkkk311, partitura.stem, edkarnie, ctime, freddio.sport, forensic911, stemisaria, holovision, jerrybanfield, lyndsaybowes, quinnertronics, artgrafiken, stem.curate, gadrian, jessica.steem, balticbadger, samuel.steem, quantumdeveloper, maruskina, nalacanecorso, axel-blaze, pecoshop, boomalex, peterpanpan, meppij, gadrian-sp, lynds, mes, poomps,