Symmetry in Integrals: Even vs. Odd Integrals
hive-128780·@mes·
0.000 HBDSymmetry in Integrals: Even vs. Odd Integrals
https://youtu.be/NbwJOQnT1eM In this video I go over the theorem on integrating symmetric functions which greatly simplifies integration. For even functions the integral from -a to a is just two times the integral from 0 to a. For odd functions, the integral from -a to a is simply zero. In this video I also provide a simple proof of this theorem while utilizing the substitution rule for integrals and properties of definite integrals. --- Watch Video On: - DTube: [https://d.tube/#!/v/mes/QmWGTkvBD7TaAkvaXBNaWQcdjefeQ5CVdnWdCRpoV7kGMu](https://d.tube/#!/v/mes/QmWGTkvBD7TaAkvaXBNaWQcdjefeQ5CVdnWdCRpoV7kGMu) - BitChute: [https://www.bitchute.com/video/mzaI5s9UHjRy/](https://www.bitchute.com/video/mzaI5s9UHjRy/) - YouTube: [https://youtu.be/NbwJOQnT1eM](https://youtu.be/NbwJOQnT1eM) Download Video Notes: https://1drv.ms/b/s!As32ynv0LoaIg4F51YbelcJqdjDD2w?e=24lko7 --- # View Video Notes Below! --- >Download these notes: Link is in video description. >View these notes as an article: https://peakd.com/@mes >Subscribe via email: http://mes.fm/subscribe >Donate! :) https://mes.fm/donate > >Reuse of my videos: >- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video. > >Fight back against censorship: >- Bookmark sites/channels/accounts and check periodically >- Remember to always archive website pages in case they get deleted/changed. > >Join my private Discord chat room: https://mes.fm/chatroom > >Check out my Reddit and Voat math forums: >- Reddit: https://reddit.com/r/AMAZINGMathStuff >- Voat: https://voat.co/v/AMAZINGMathStuff > >Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook >Follow along my epic video series: >- #MESScience: https://mes.fm/science-playlist >- #MESExperiments: https://peakd.com/mesexperiments/@mes/list >- #AntiGravity: https://peakd.com/antigravity/@mes/series >-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept! >- #FreeEnergy: https://mes.fm/freeenergy-playlist > >--- > >NOTE #1: If you don't have time to watch this whole video: > >- Skip to the end for Summary and Conclusions (if available) >- Play this video at a faster speed. >-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed) >-- Try 4X+ speed by browser extensions or modifying source code. >-- **Browser extension recommendation: https://mes.fm/videospeed-extension** >-- See my tutorial to learn more: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website >- Download and read video notes. >- Read notes on the Hive blockchain #Hive >- Watch the video in parts. > >NOTE #2: If video volume is too low at any part of the video: > >- Download this browser extension recommendation: https://mes.fm/volume-extension --- # Symmetry in Integrals  ## Integrals of Symmetric Functions Theorem Suppose f is continuous on [-a, a]. (a) If f is even, meaning f(-x) = f(x), then: 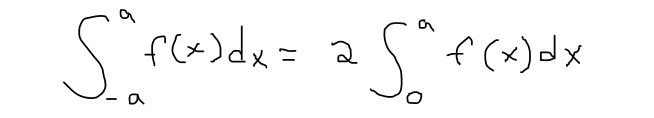 (b) If f is odd, meaning f(-x) = - f(x), then: 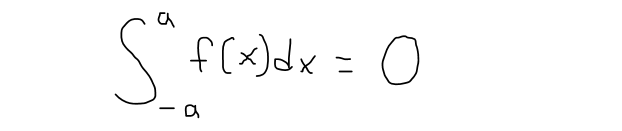 **Proof:** 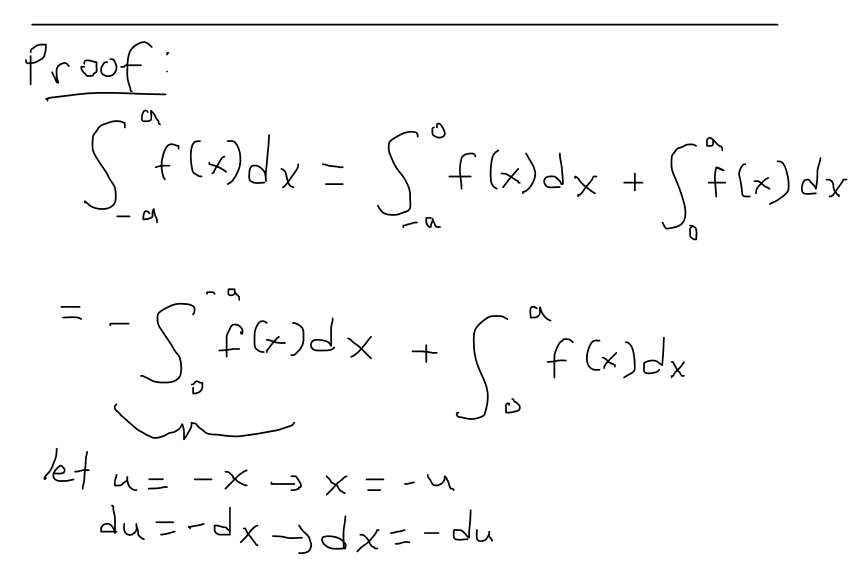 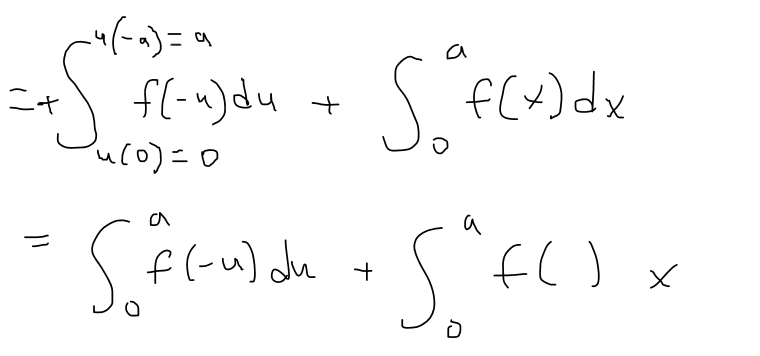  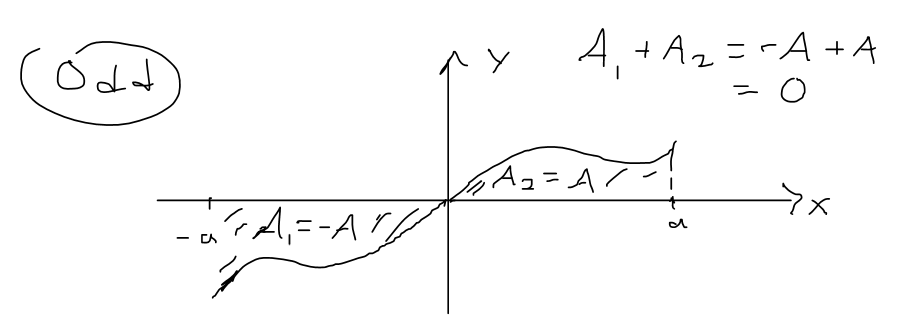
👍 davidlionfish, edkarnie, stemisaria, vlemon, delso, zemiatin, koskl, proboards, themanny, fulltimebot73, fulltimebot6, fulltimebot7, fulltimebot23, fulltimebot31, fulltimebot43, fulltimebot52, memen, fulltimebot16, fulltimebot18, fulltimebot4, fulltimebot27, fulltimebot14, fulltimebot65, supersoldier, fulltimebot, lizardslayer, proboards2, fulltimebot62, fulltimebot50, fulltimebot5, fulltimebot70, fulltimebot75, fulltimebot47, fulltimebot10, fulltimebot12, fulltimebot17, fulltimebot22, fulltimebot40, fulltimebot42, fulltimebot63, teacherspet, curie, gunthertopp, bestofph, skycae, kendallron, pinas, thelordsharvest, postpromoter, alaqrab, steemiteducation, crystalhuman, edu-venezuela, epicdice, justtryme90, roseri, affiedalfayed, misterbob, blue-pencil, nateaguila, schoolforsdg4, esaia.mystic, sandracabrera, vittoriozuccala, alanasteemit, srijana-gurung, jk6276, azizbd, gmedley, reizak, womenempowerment, aboutyourbiz, socialbot, ph1102, call-me-howie, kenadis, foxyspirit, mowemu, randomblock1, zerotoone, musicvoter, arnilarn, brutledge, steemegg, goblinknackers, lordjames, carn, javier.dejuan, bitrocker2020, florian-glechner, eztechwin, didic, c0wtschpotato, gabrielatravels, takowi, ambitiouslife, schroders, zipporah, cheese4ead, breakout101, cryptofiloz, revo, fernando.lubezki, healthexpert, shaunmza, stickchumpion, reverseacid, blueorgy, briggsy, pechichemena, bscrypto, newtrailers, bradleyarrow, phgnomo, iamjadeline, bluemaskman, motherofalegend, bflanagin, arnel, upme, stahlberg, drmake, upfundme, begood2me, joshmania, modernzorker, nehomar, soufianechakrouf, gravii4, ufm.pay, uwelang, pulleyhead, mahdiyari, torico, onemedia, mxzn, stayoutoftherz, tazbaz, hijosdelhombre, spoke, travisung, dashfit, steemjet, chris4210, sustainablyyours, bil.prag, camiloferrua, sankysanket18, misan, myfreebtc, hairgistix, musicvoter2, the.success.club, steveconnor, diana.catherine, locikll, allcapsonezero, hansmast, psygambler, vact, apsu, operahoser, bloom, braveboat, tommyl33, hendrikdegrote, itchyfeetdonica, palasatenea, tombstone, kimzwarch, misia1979, featheredfriend, anwenbaumeister, driptorchpress, teukurival, nutman, pushpedal, hanggggbeeee, ilazramusic, iansart, rambutan.art, gwilberiol, minimining, bernardino, positiveninja, jancharlest, dronegraphica, filosof103, bibkchhetri, ppss, deeanndmathews, kalinka, gordon92, orthodoxnudism, fearlessgu, qberry, cryptononymous, venalbe, tngflx, garudi, dokter-purnama, trang, solarphasing, dacx, deathlyhorror, outtheshellvlog, cecilian, matt-a, blewitt, ilovecryptopl, honeycup-waters, yangoldberg, redcube, forester-joe, chickenmeat, neumannsalva, khan.dayyanz, kibela, battebilly, dechastre, miroslavrc, kylealex, rem-steem, shimozurdo, yourtop3, freetissues, felt.buzz, jlsplatts, lightflares, saboin, marcocasario, kork75, rbalzan79, thepeakstudio, punchline, hanshotfirst, theregularguy, steemwizards, jimshorts, nerdnews, vera-vaders-ea, karaoke1850, notb4mycoffee, silverwhale, hanzappedfirst, weirdnews, kylo-ren, hanshotfirst-sm, techslut, thatindianlady, majes.tytyty, robibasa, ibt-survival, ralph-rennoldson, sanderjansenart, bluefinstudios, loliver, titan-c, drlobes, reggaesteem, justinparke, sweetpea, ericburgoyne, rival, pladozero, lextenebris, lordvader, olusolaemmanuel, peaceandwar, thescubageek, fatkat, binkyprod, danile666, alvin0617, prapanth, buttcoins, dearw, macoolette, leilanyarevalo, vegan.niinja, danaedwards, shinedojo, knightbjj, mammasitta, massivevibration, bennettitalia, steem.consultant, vaultec, steveblucher, eric-boucher, nicole-st, esthersanchez, deisip67, rajib2k5, lk666, oghie, genoner, wishmaiden, drawmeaship, alinabarbu, flatman, xanderslee, nwjordan, indayclara, guada1, dream.trip, jagged, fulltimebot57, fulltimebot29, fulltimebot15, fulltimebot37, fulltimebot66, fulltimebot45, fulltimebot56, fulltimebot33, fulltimebot61, fulltimebot60, fulltimebot64, fulltimebot34, exterminator, fulltimeangel, fulltimebot24, fulltimebot11, fulltimebot1, fulltimebot2, fulltimebot30, fulltimebot32, fulltimebot25, fulltimebot55, fulltimebot72, fulltimebot74, goldenchild, perfectstorm, townmayor, mes,