Point-To-Line Distance Formula: Algebraic Proof
mathematics·@mes·
0.000 HBDPoint-To-Line Distance Formula: Algebraic Proof
https://youtu.be/tngPrM2d-OM In this video I go over deriving the formula for the shortest distance between a point and a line. There are several different ways of deriving this, and in this video I use an algebraic derivation. This method involves using the fact that the shortest distance between a point and a line is the line that is perpendicular to the other line. Thus both lines are negative reciprocals of each other. Combined with the Pythagorean theorem to obtain the square of the distance in determines of the squares of the differences in x and y, we can then play around with some algebra to obtain our final formulation. Note the general proof used in this video involves a derivation which is not valid for vertical or horizontal lines BUT the final result still holds true nonetheless! This is actually a very interesting result and illustrates how we must always use mathematical rigor regardless of whether the final formula is valid for cases that weren't valid in the proof methodology; so make sure to watch this video! Watch Video On: - BitChute: [https://www.bitchute.com/video/1L5Z9FfNjir5/](https://www.bitchute.com/video/1L5Z9FfNjir5/) - 3Speak: [https://3speak.tv/watch?v=mes/xlgrdbnc](https://3speak.tv/watch?v=mes/xlgrdbnc) - DTube: [https://d.tube/#!/v/mes/tigaernv](https://d.tube/#!/v/mes/tigaernv) - YouTube: [https://youtu.be/tngPrM2d-OM](https://youtu.be/tngPrM2d-OM) Download PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIhv8AcV6RCgPi8zuO4g --- # View Video Notes Below! --- >Download these notes: Link is in video description. >View these notes as an article: https://peakd.com/@mes >Subscribe via email: http://mes.fm/subscribe >Donate! :) https://mes.fm/donate >Buy MES merchandise! https://mes.fm/store > >Reuse of my videos: >- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video. > >Fight back against censorship: >- Bookmark sites/channels/accounts and check periodically >- Remember to always archive website pages in case they get deleted/changed. > >Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook >Subscribe to MES Truth: https://mes.fm/truth > >Join my forums! >- Hive community: https://peakd.com/c/hive-128780 >- Reddit: https://reddit.com/r/AMAZINGMathStuff >- Voat: https://voat.co/v/AMAZINGMathStuff >- Discord: https://mes.fm/chatroom > >Follow along my epic video series: >- #MESScience: https://mes.fm/science-playlist >- #MESExperiments: https://peakd.com/mesexperiments/@mes/list >- #AntiGravity: https://peakd.com/antigravity/@mes/series >-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept! >- #FreeEnergy: https://mes.fm/freeenergy-playlist >- #PG (YouTube-deleted series): https://peakd.com/pg/@mes/videos > >--- > >NOTE #1: If you don't have time to watch this whole video: > >- Skip to the end for Summary and Conclusions (if available) >- Play this video at a faster speed. >-- TOP SECRET LIFE HACK: Your brain gets used to faster speed! >-- **Browser extension recommendation: https://mes.fm/videospeed-extension** >-- See my tutorial to learn more: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website >- Download and read video notes. >- Read notes on the Hive blockchain #Hive >- Watch the video in parts. >-- Timestamps of all parts are in the description. > >Browser extension recommendations: > >- Increase video audio: https://mes.fm/volume-extension >- Text to speech: https://mes.fm/speech-extension --- # Point-to-Line Distance Formula: Algebraic Proof 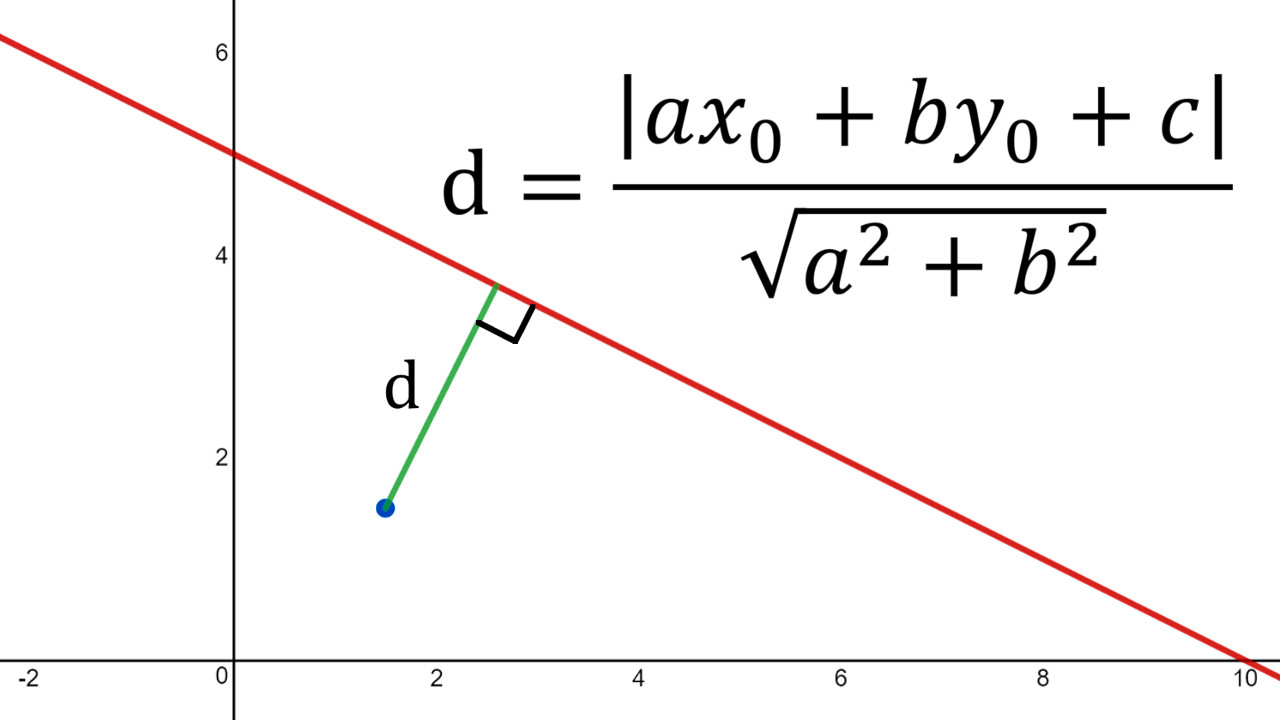 Recall the equation of a line, as well as the fact that a perpendicular line has a slope which is a negative reciprocal to the other line. 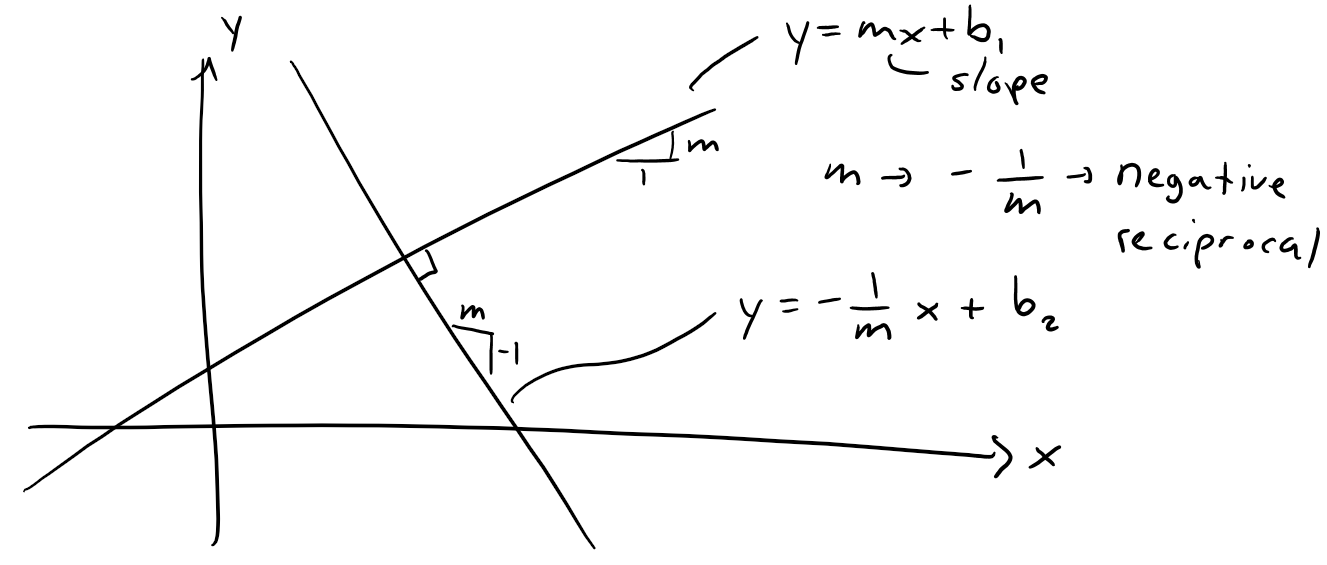 The general equation of a line is written as follows: 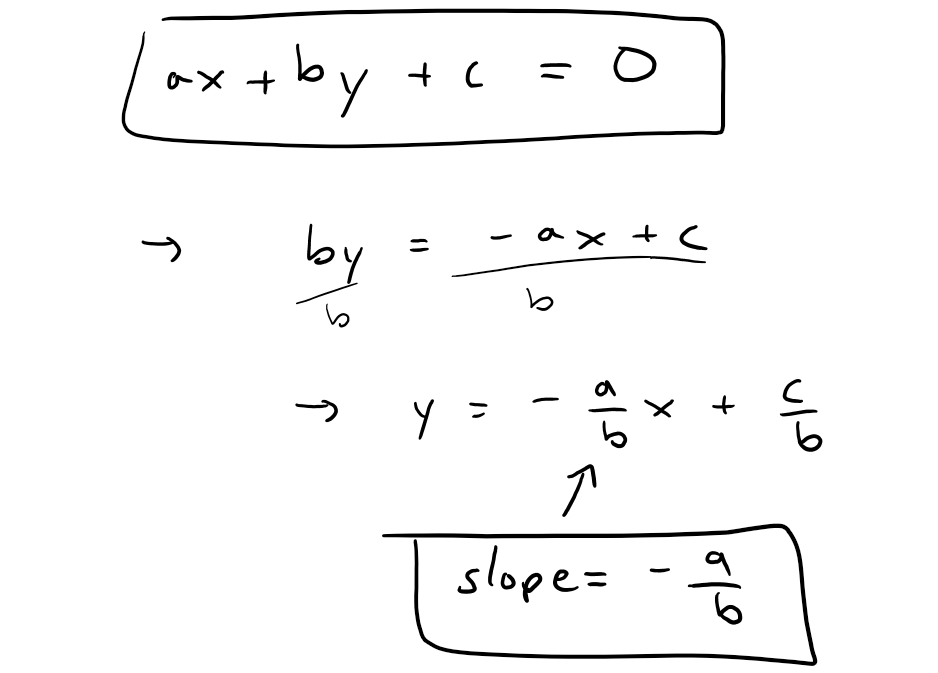 Where: a, b, c are constants. Now, if we wanted to find the shortest distance from a point to a line, we have 3 different scenarios we have to account for: **1. Distance from a Horizontal Line, a = 0.** 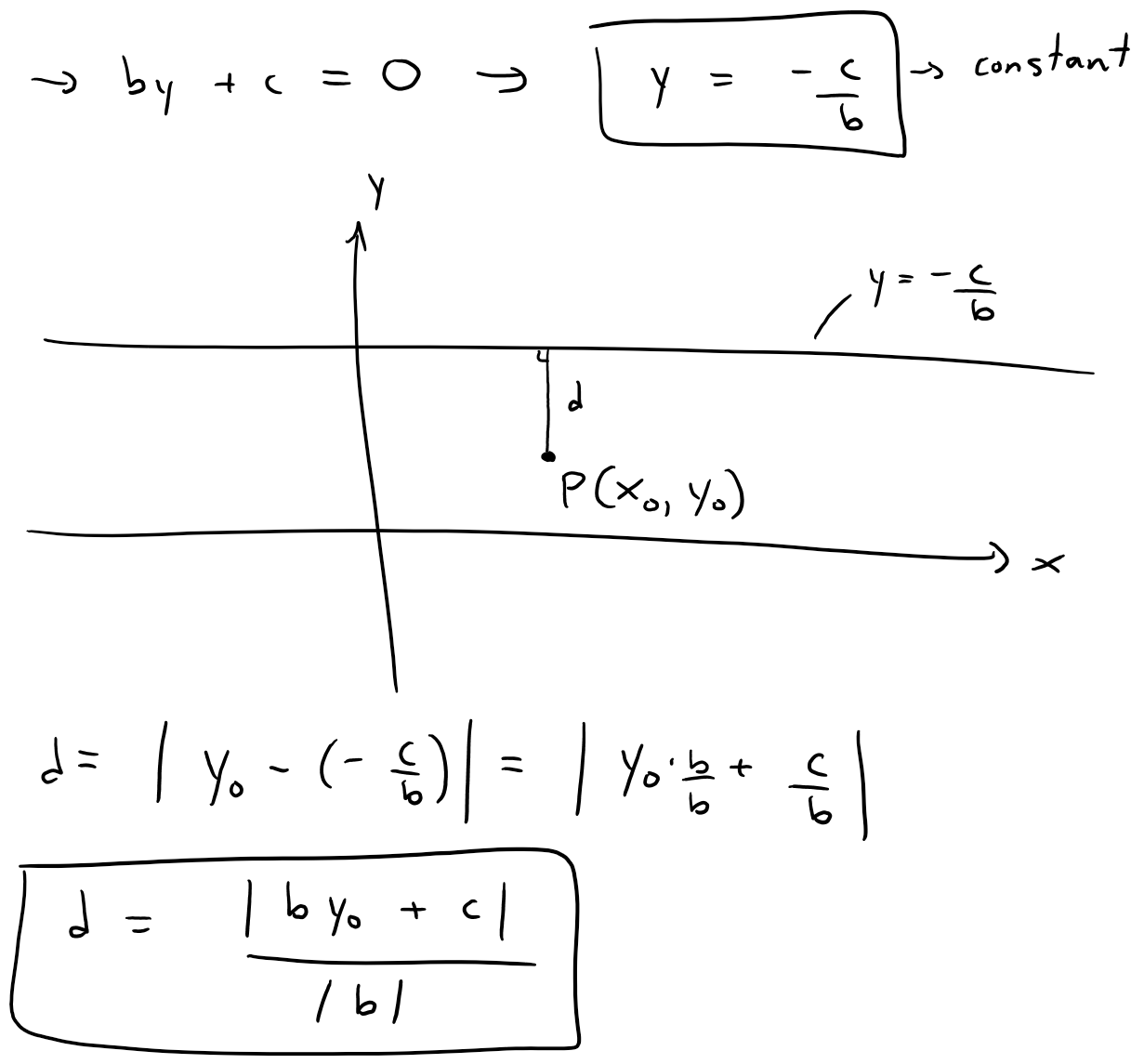 **2. Distance from a Vertical Line, b = 0.** 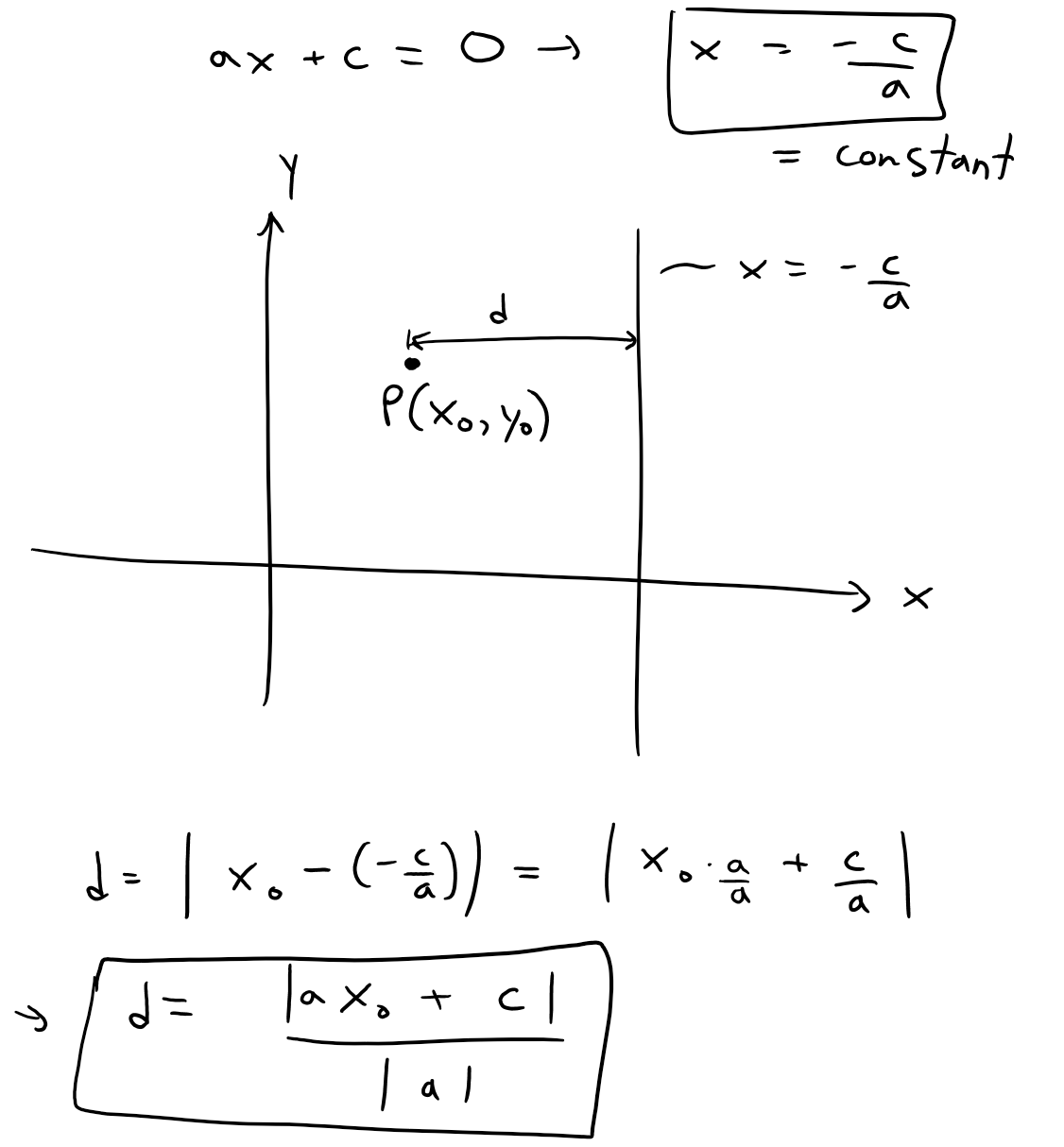 **3. Distance to a Slanted Line, i.e. a and b are non-zero.** Note: While this proof is not valid for when a or b equal 0 (because the negative reciprocals would involve dividing by 0 or by infinity which are not defined), the final result nonetheless gives the same result for both horizontal and vertical lines! The shortest distance from a point to a line is the line segment that is perpendicular to the line, thus their slopes are negative reciprocals of each other! 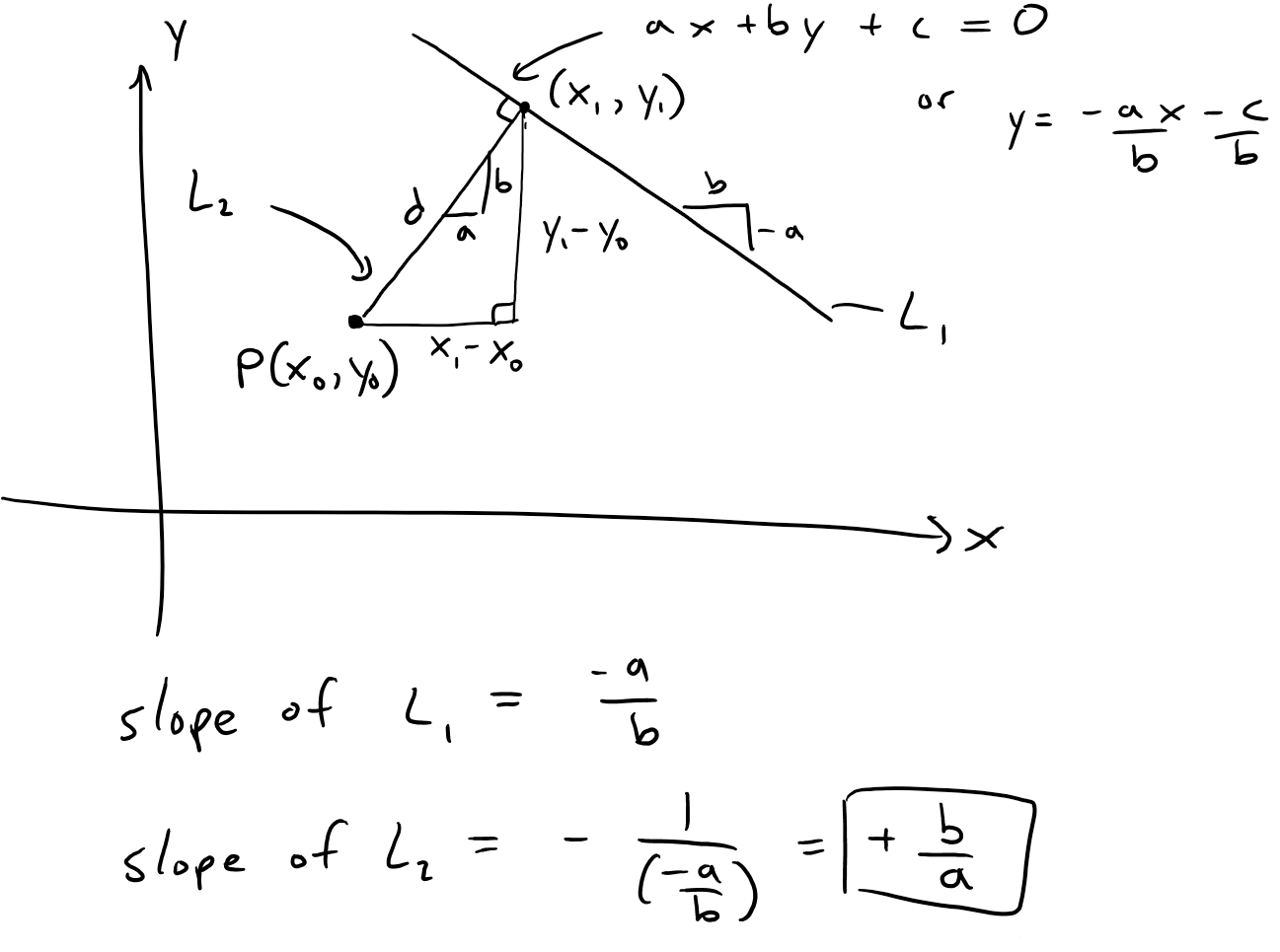 Also note that the slope of L<sub>2</sub> is just the rise over run of the two points. 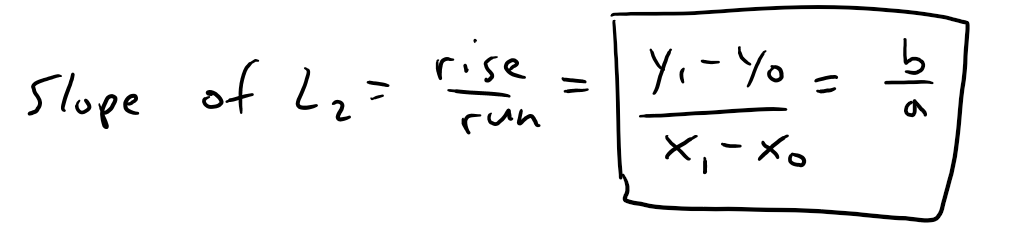 From Pythagoras we have: 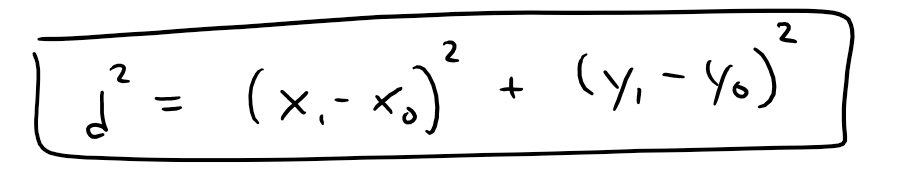 Now what we want to do is to find an expression that for distance, d, that removes x<sub>1</sub> and y<sub>1</sub> . One way to go about this is to rearrange the above slope formula to maintain "squared differences" as in the distance formula. 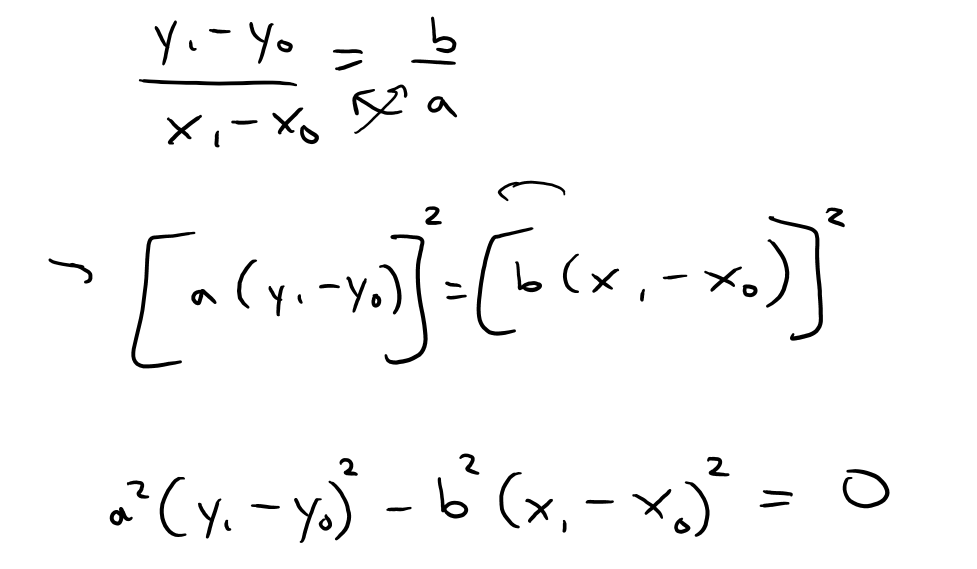 Note that this formula isn't that useful, but luckily there is another way to obtain squared differences! 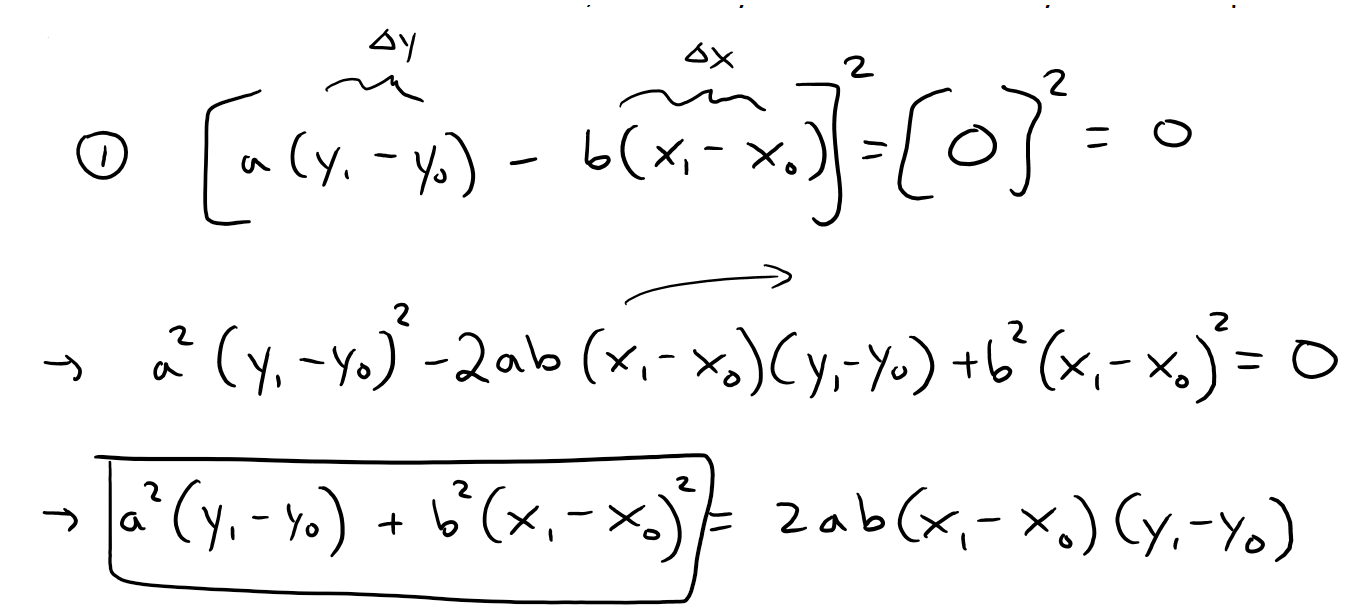 Now this is actually very useful, because we can obtain "2ab…" term in multiple different methods, such as: 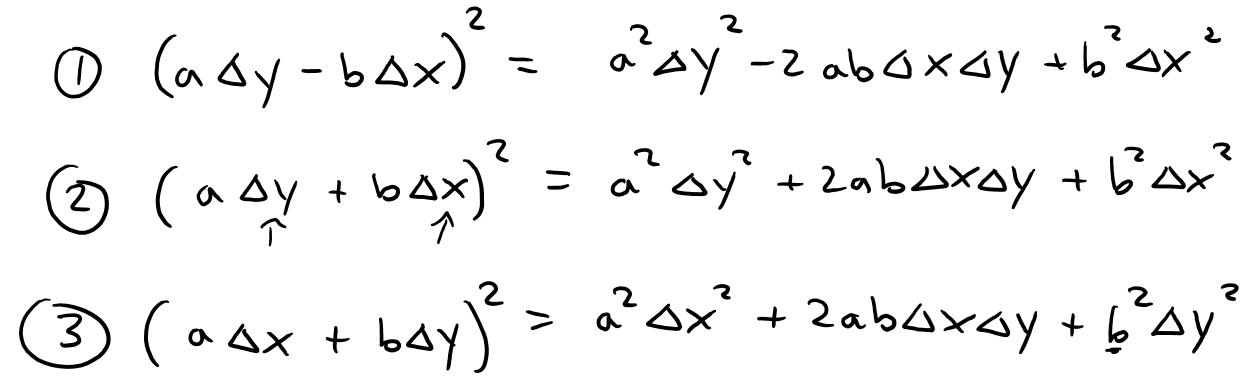 Thus if we use the 3rd option, we can have a common factor of (a<sup>2</sup> + b<sup>2</sup>) as shown below, # Amazing! 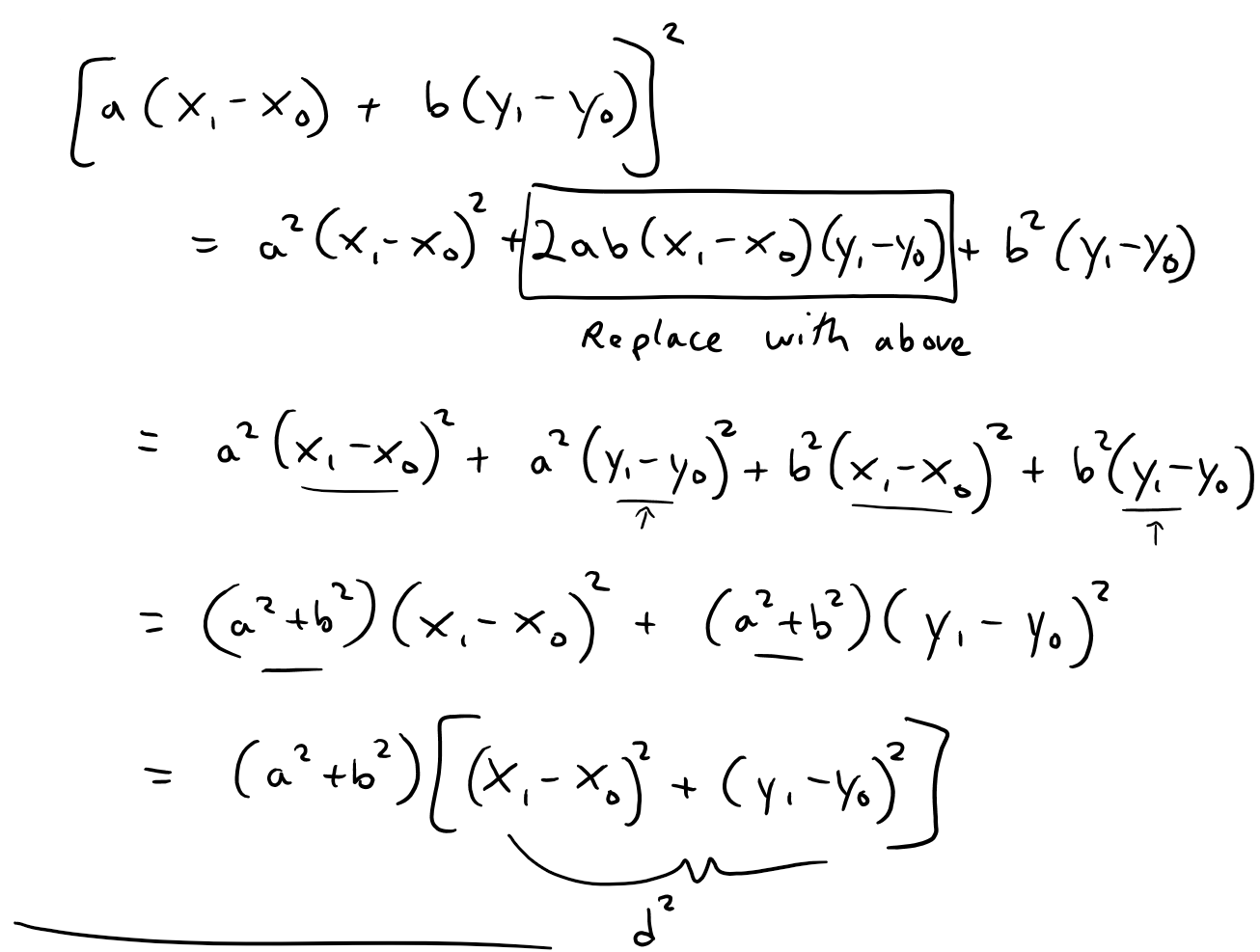 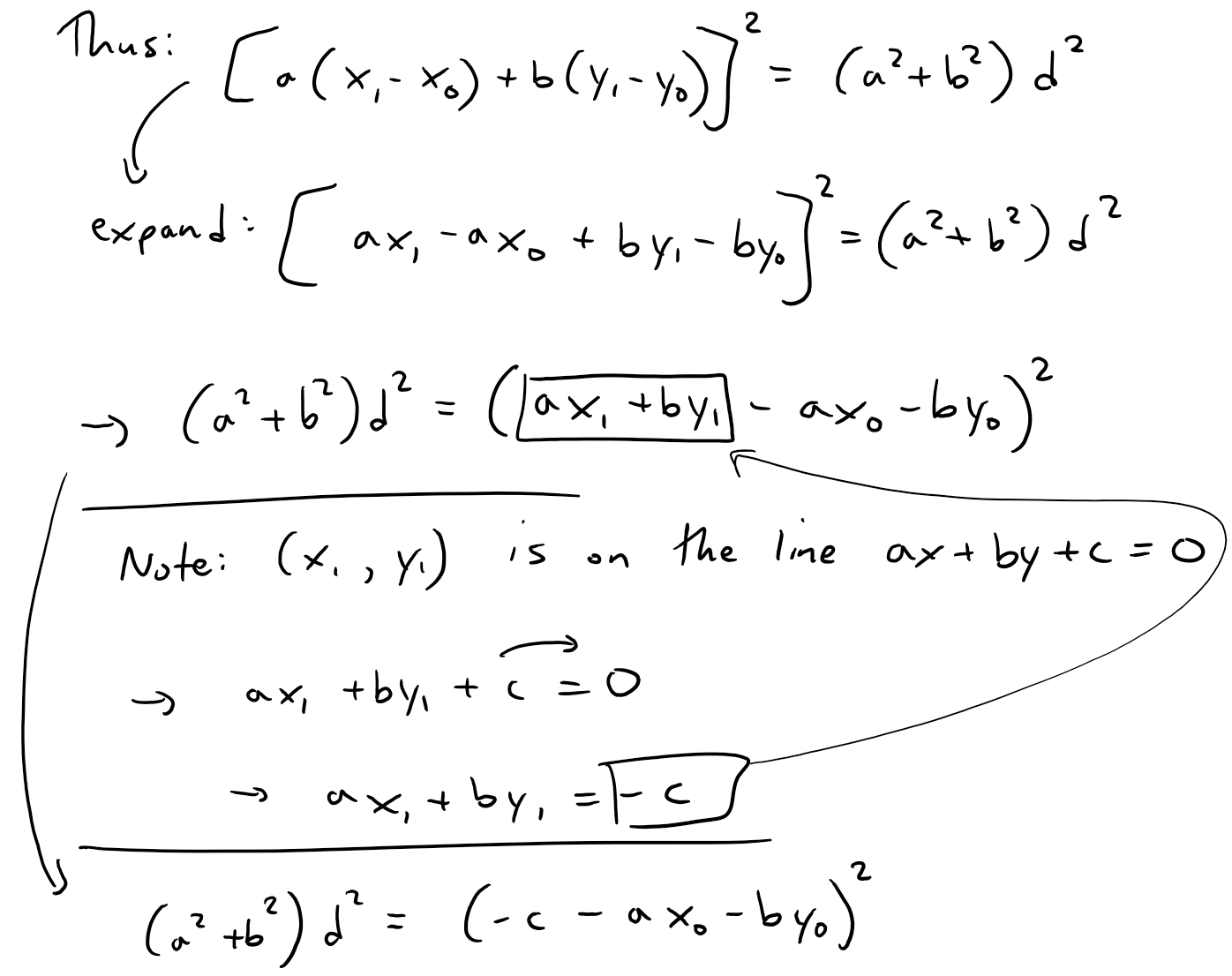 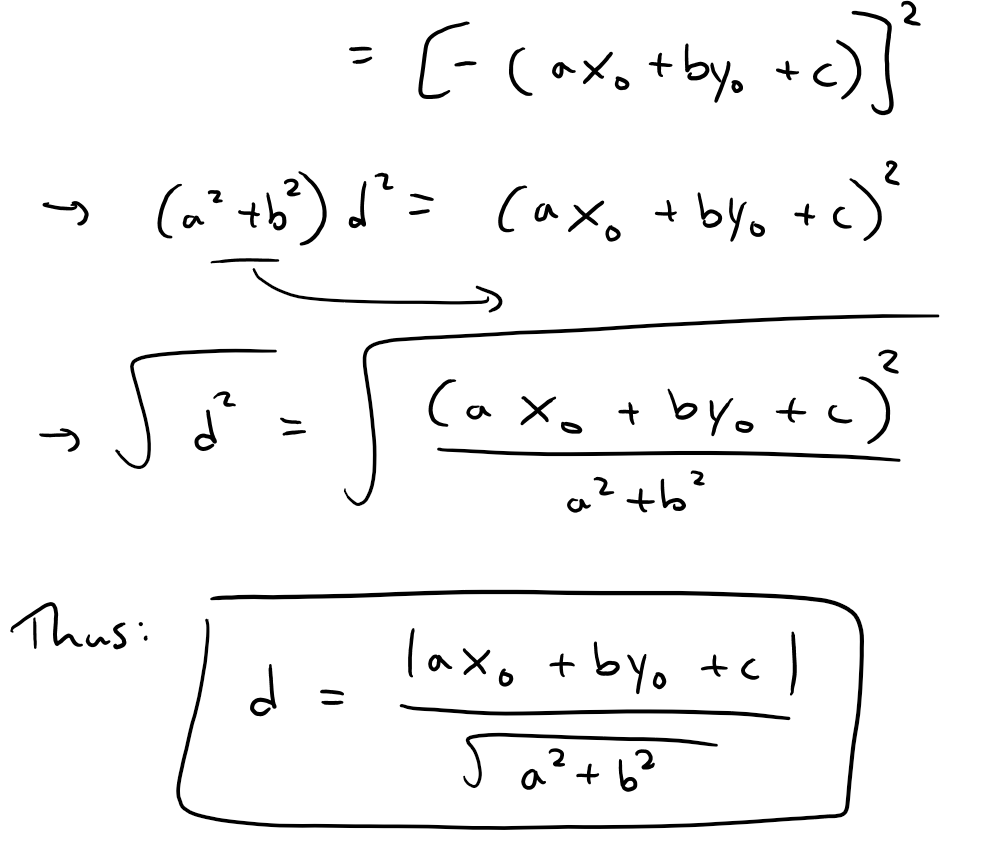 Note that as explained above, this formula nonetheless works for distances to horizontal or vertical lines, even though the proof was not valid for them. 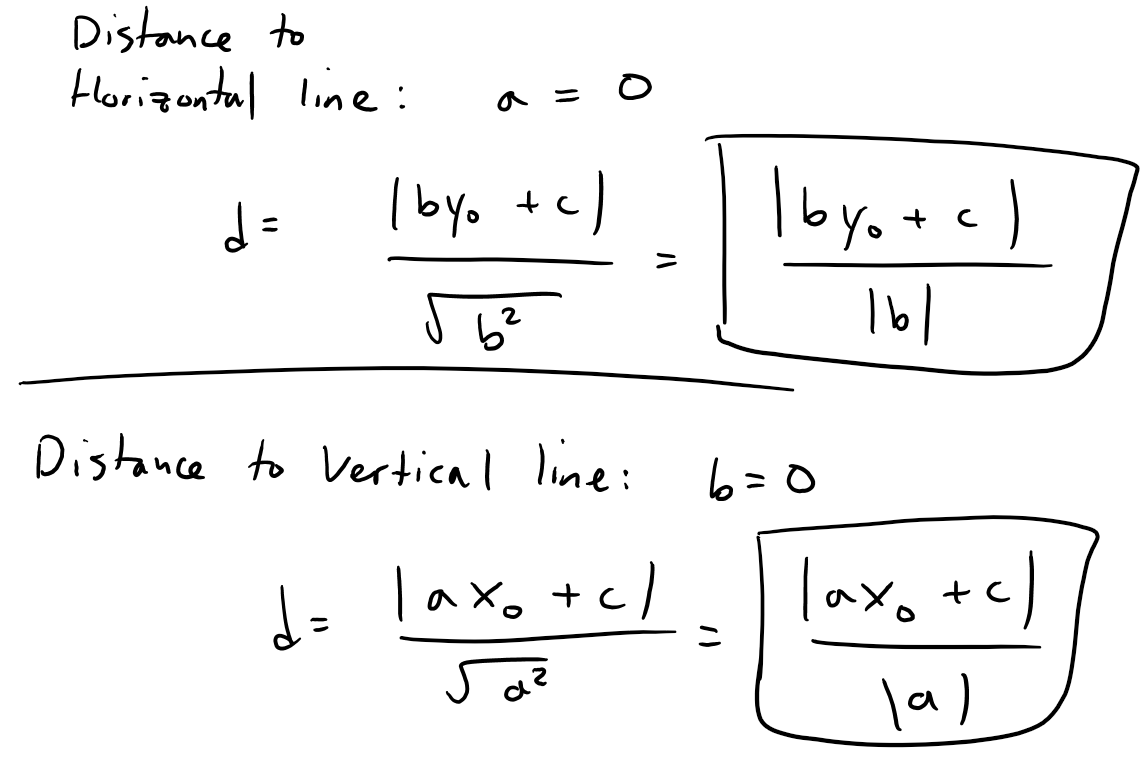 This is actually a great example of showing that we always need to apply mathematical rigor in our derivations regardless of whether the end result will be the same, because not always will we be this lucky, and may end up with large errors that build up! # LifeLessonForEverything