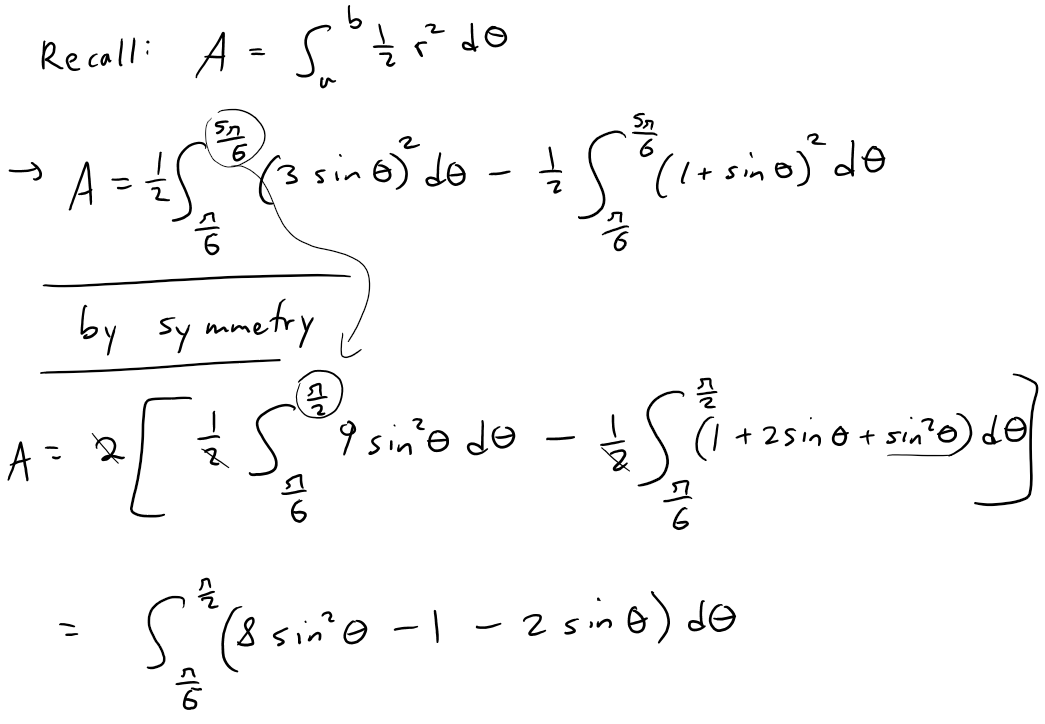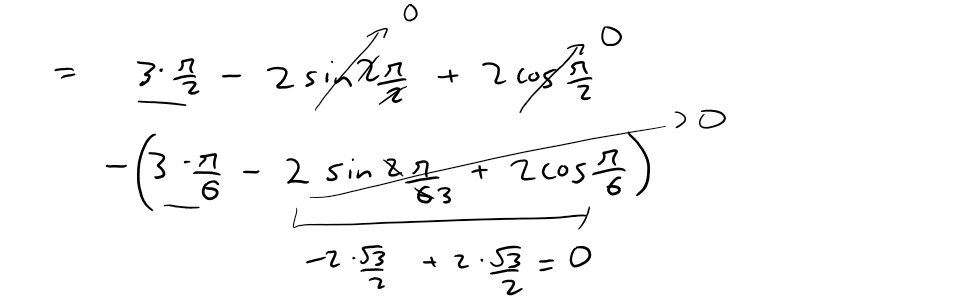Polar Coordinates: Area: Example 2: Cardioid and Circle
mathematics·@mes·
0.000 HBDPolar Coordinates: Area: Example 2: Cardioid and Circle
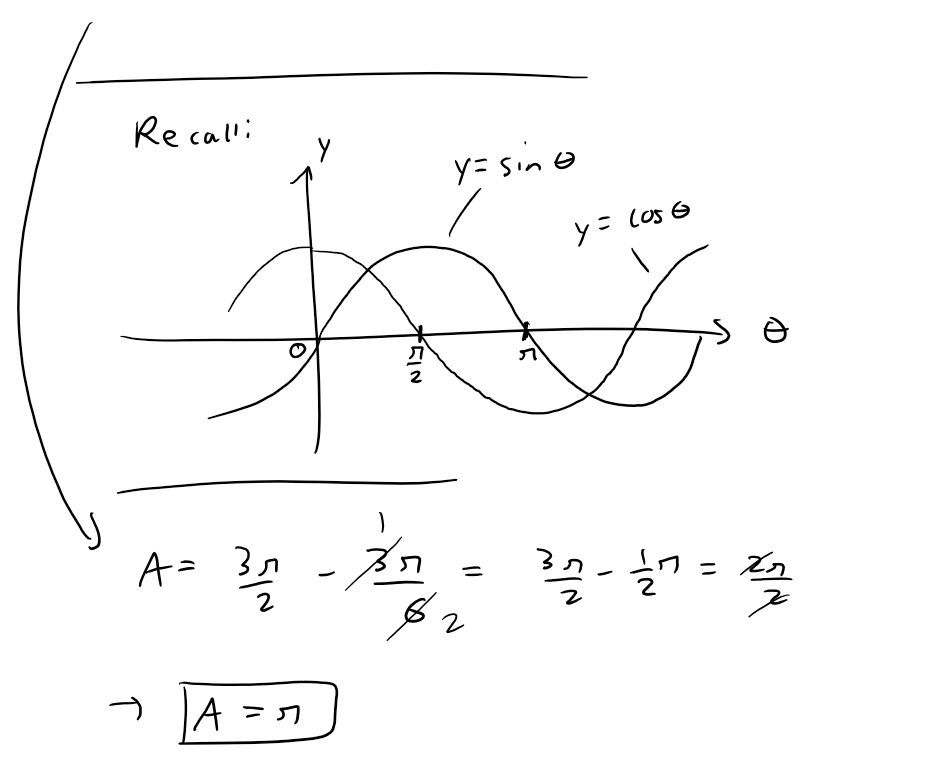
https://youtu.be/vSzxzNn3EiA In this video I go over another example on calculating the area of polar curves and this time find the area enclosed by a circle yet separated by a cardioid. The Cardioid, or Heart in Greek, is the same formula I had previously graphed in my earlier example video. To save time, I plot both of the graphs together by using the Desmos calculator to obtain the resulting area we need to calculate. The first step in solving for the area is to find the points at which they intersect. From there we can apply the formula for the area of a polar curve which I covered in my earlier video, but this time we solve for the area of a polar circle, and then subtract from it the area of the polar cardioid. This is a very important video in understanding how to go about solving in detail the area enclosed by two polar curves, so make sure to watch this video! Watch Video On: - 3Speak: [https://3speak.tv/watch?v=mes/uhjxusmt](https://3speak.tv/watch?v=mes/uhjxusmt) - BitChute: [https://www.bitchute.com/video/Pg69pmLYeSGy/](https://www.bitchute.com/video/Pg69pmLYeSGy/) - DTube: [https://d.tube/#!/v/mes/ss1oi8l6](https://d.tube/#!/v/mes/ss1oi8l6) - YouTube: [https://youtu.be/vSzxzNn3EiA](https://youtu.be/vSzxzNn3EiA) Download PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIhvVAKCYLCqdXeyXJow --- # View Video Notes Below! --- >Download these notes: Link is in video description. >View these notes as an article: https://peakd.com/@mes >Subscribe via email: http://mes.fm/subscribe >Donate! :) https://mes.fm/donate >Buy MES merchandise! https://mes.fm/store >More links: https://linktr.ee/matheasy > >Reuse of my videos: >- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video. > >Fight back against censorship: >- Bookmark sites/channels/accounts and check periodically >- Remember to always archive website pages in case they get deleted/changed. > >Recommended Books: >- "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook > >Subscribe to MES Truth: https://mes.fm/truth > >Join my forums! >- Hive community: https://peakd.com/c/hive-128780 >- Reddit: https://reddit.com/r/AMAZINGMathStuff >- Discord: https://mes.fm/chatroom > >Follow along my epic video series: >- #MESScience: https://mes.fm/science-playlist >- #MESExperiments: https://peakd.com/mesexperiments/@mes/list >- #AntiGravity: https://peakd.com/antigravity/@mes/series >-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept! >- #FreeEnergy: https://mes.fm/freeenergy-playlist >- #PG (YouTube-deleted series): https://peakd.com/pg/@mes/videos > >--- > >NOTE #1: If you don't have time to watch this whole video: > >- Skip to the end for Summary and Conclusions (if available) >- Play this video at a faster speed. >-- TOP SECRET LIFE HACK: Your brain gets used to faster speed! >-- MES tutorial: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website >- Download and read video notes. >- Read notes on the Hive blockchain #Hive >- Watch the video in parts. >-- Timestamps of all parts are in the description. > >Browser extension recommendations: > >- Increase video speed: https://mes.fm/videospeed-extension >- Increase video audio: https://mes.fm/volume-extension >- Text to speech: https://mes.fm/speech-extension >--Android app: https://mes.fm/speech-android --- # Example Find the area of the region that lies inside the circle r = 3sinθ and outside the cardioid r = 1 + sinθ. 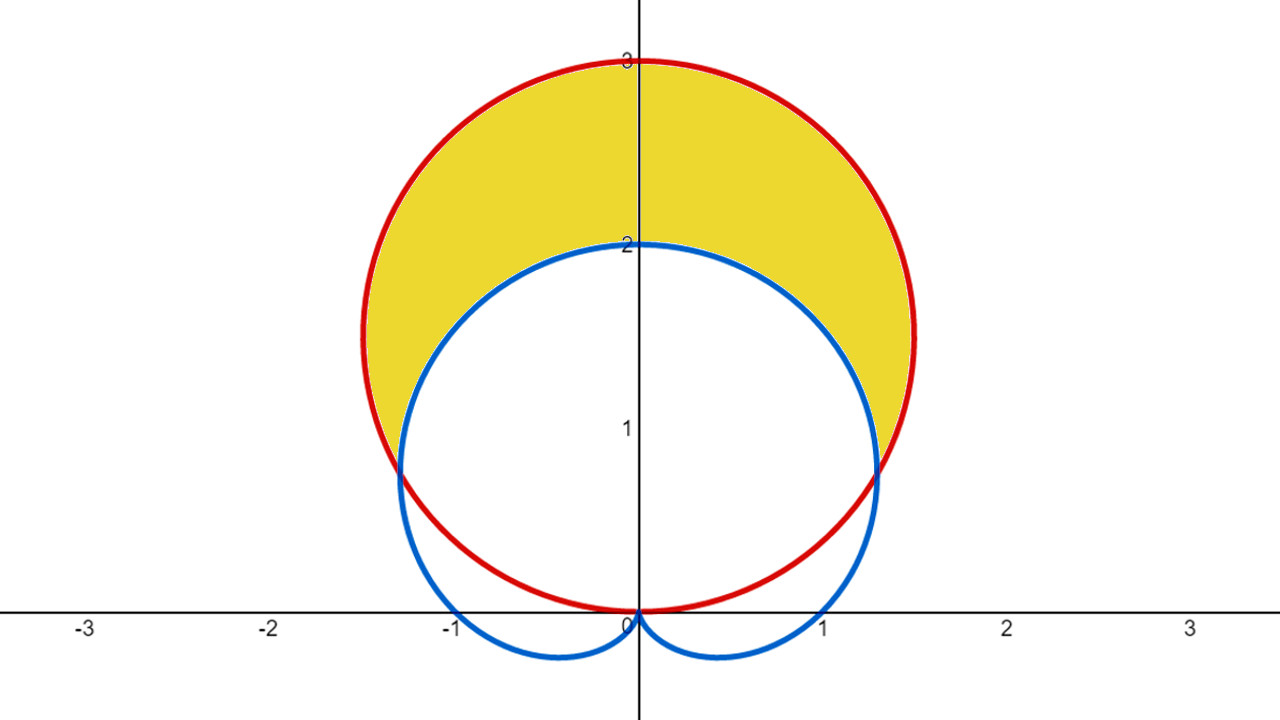 ## Solution The cardioid (see video Polar Coordinates: Example 7) and the circle are graphed below: https://www.desmos.com/calculator/sui9fimg2l 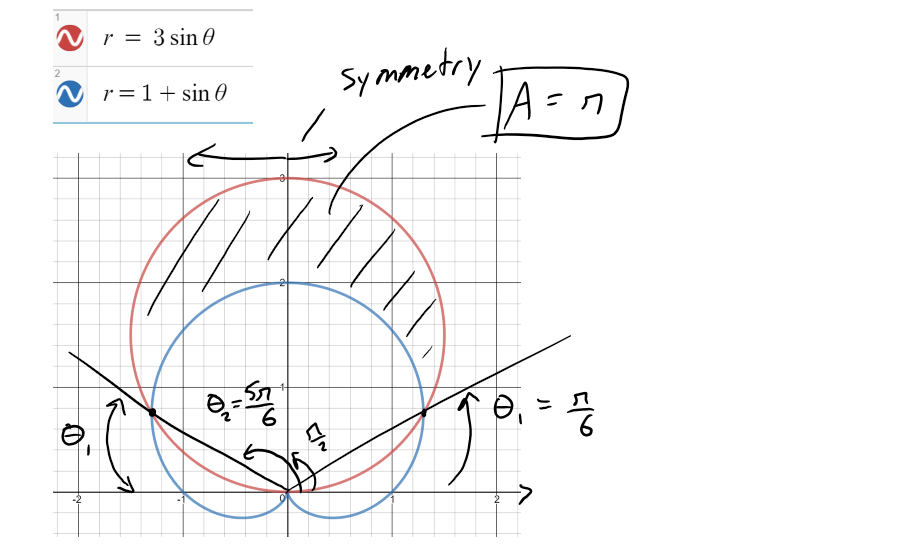 We need to find the points in which the circle and cardioid intersect: 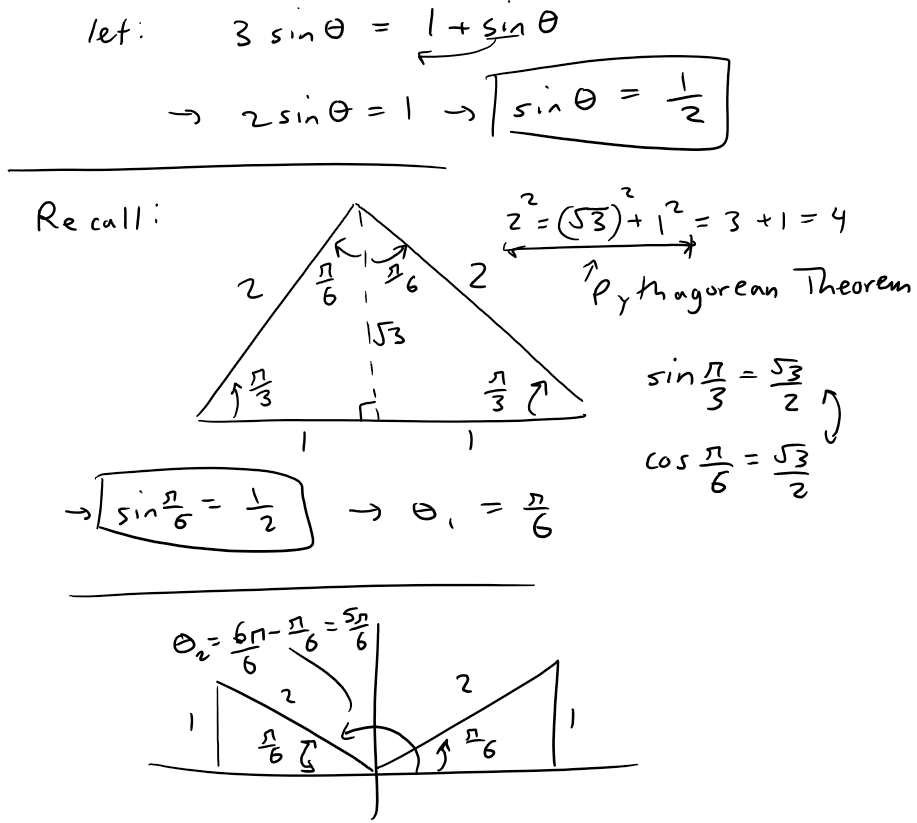 The area can be obtained by subtracting the area inside the cardioid from θ = π/6 to θ = 5π/6 from the area inside the circle from π/6 to 5π/6.