<div class="text-justify">

![1.PNG](https://cdn.steemitimages.com/DQmQQDqMYR2xRGUMpXQCiePT3FnBk4nPVPZ3JHMQEfvunVF/1.PNG)

![1.PNG](https://cdn.steemitimages.com/DQmPoMv1HFZPeh7PePSDqYhAepMPk48tp1yM7BxRRWxLe6a/1.PNG)

Saludos a toda la comunidad científica y académica de Steemit, en esta oportunidad se da continuidad a la temática de **Funciones**, esta vez abordando el tópico de la **Función Inversa**, un saber matemático de gran relevancia en la Matemática. Para ello debemos recordar algunos aspectos relacionados, en primer lugar, tiene que ver con la noción de *inverso*, en este caso hablando genéricamente nos referimos al *elemento simétrico*, concepto que acompaña muchas definiciones en el ámbito de la Matemática, presentado en su formalidad desde la perspectiva algebraica. Para el caso de las *operaciones matemáticas* **adición** y **multiplicación** este elemento se particulariza con nombres específicos, para la primera se denomina *elemento opuesto* y para la segunda *elemento inverso*, y los cuales al *operar* con su elemento espejo, por llamarlo de alguna forma nos resulta el *elemento neutro*.

En el caso de las funciones, ocurre un hecho similar de una manera que se detallará en la presente publicación, asimismo, se abordará con las formalidad del caso y fundamentalmente desde la visión algebraica su definición, propiedades, representación gráfica, al tiempo que se planteará un ejemplo que permita visualizar la aplicación del concepto de *función inversa*. Otro de los aspectos que recomiendo tener presentes para la comprensión del saber que se compartirá a continuación tiene que ver con las *relaciones inversas* - [ver aquí](https://steemit.com/spanish/@reinaseq/relaciones-binarias-nociones-fundamentales) - recordemos que **toda función es una relación aunque no toda relación es una función**, por lo cual se verifica la misma definición salvo que en el caso de las funciones como ya sabemos, deben cumplir con las condiciones de *existencia de imagen* y *unicidad de imagen*.

Se invita a los lectores al disfrute académico de las nociones que se compartirán a continuación. Comencemos.

![2.PNG](https://cdn.steemitimages.com/DQmSgmmgM7rC1CPgLucQpCVkJ2eqqcn5eNHasGmcn9TMfhk/2.PNG)

La *función inversa* también se conoce como *función recíproca* o *función invertible* y como ya se ha indicado, genéricamente hablando como *función simétrica*, cuya definición formal, es

Sean la funciones *f:A⟶B* se define la *función inversa* de la siguiente manera

![2.PNG](https://cdn.steemitimages.com/DQmd3f6bunVW8DioTxHavN9BYStyCTJ3j7teB5ynjnta8zG/2.PNG)

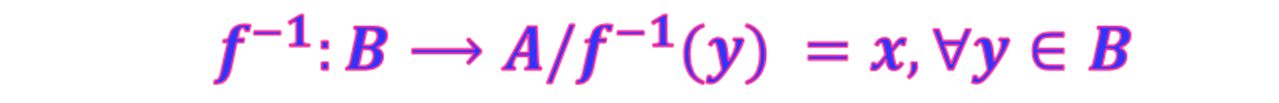
Gráficamente se representa como sigue

![3.PNG](https://cdn.steemitimages.com/DQmaBDswTX8jhiqV4LXt224UyPuFubJsVFF2uv2xHJif2XJ/3.PNG)

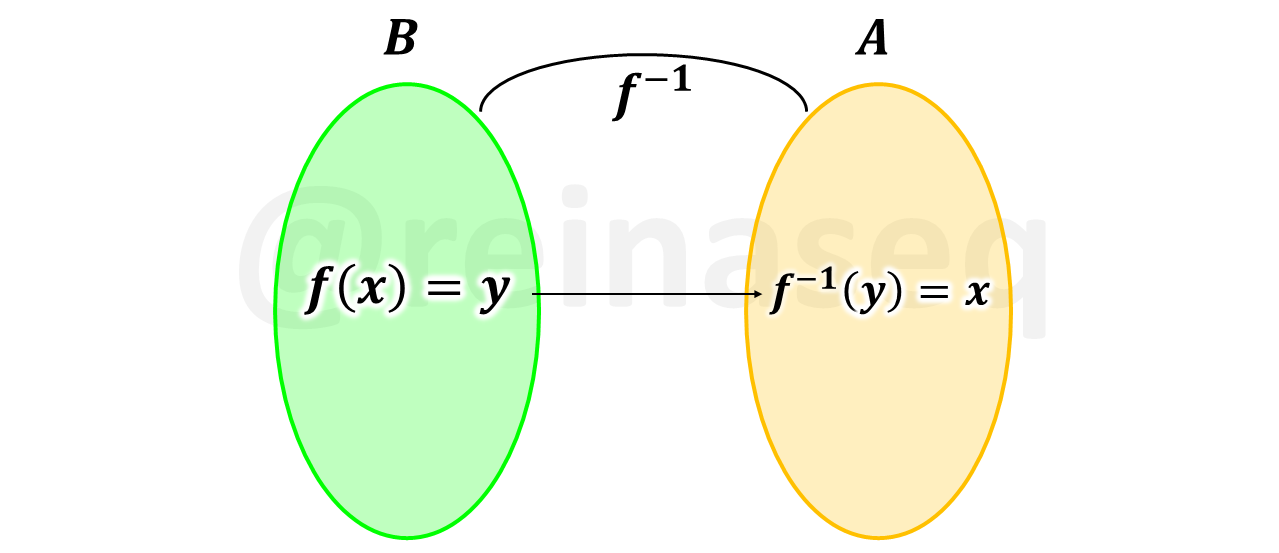
Recordando que la **función identidad** - [ver aquí](https://steemit.com/spanish/@reinaseq/funciones-nociones-fundamentales) – se considera *elemento neutro* de las funciones, entonces tenemos que la función inversa verifica lo siguiente

![4.PNG](https://cdn.steemitimages.com/DQmUQdKWghDZjJHgnNAAuvRVSHFcoMdj6hhu9YAX6CLhKD4/4.PNG)

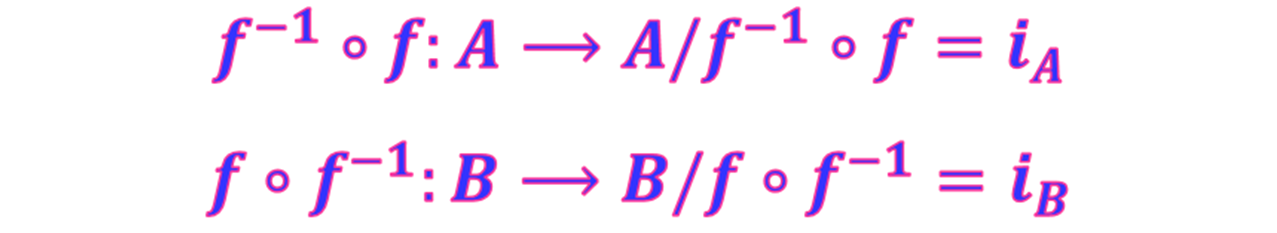
Lo anterior se puede ampliar y comprender en las siguientes representaciones gráficas

![5.PNG](https://cdn.steemitimages.com/DQmaffBYuyTw9vGBKvmFckFGPEG7Z8JAbp23E1AJv1175n1/5.PNG)

![6.PNG](https://cdn.steemitimages.com/DQmVLhY68vF4graBX2ZujwW4eYfBPMNwMhMCqsCQ7S3QHHT/6.PNG)

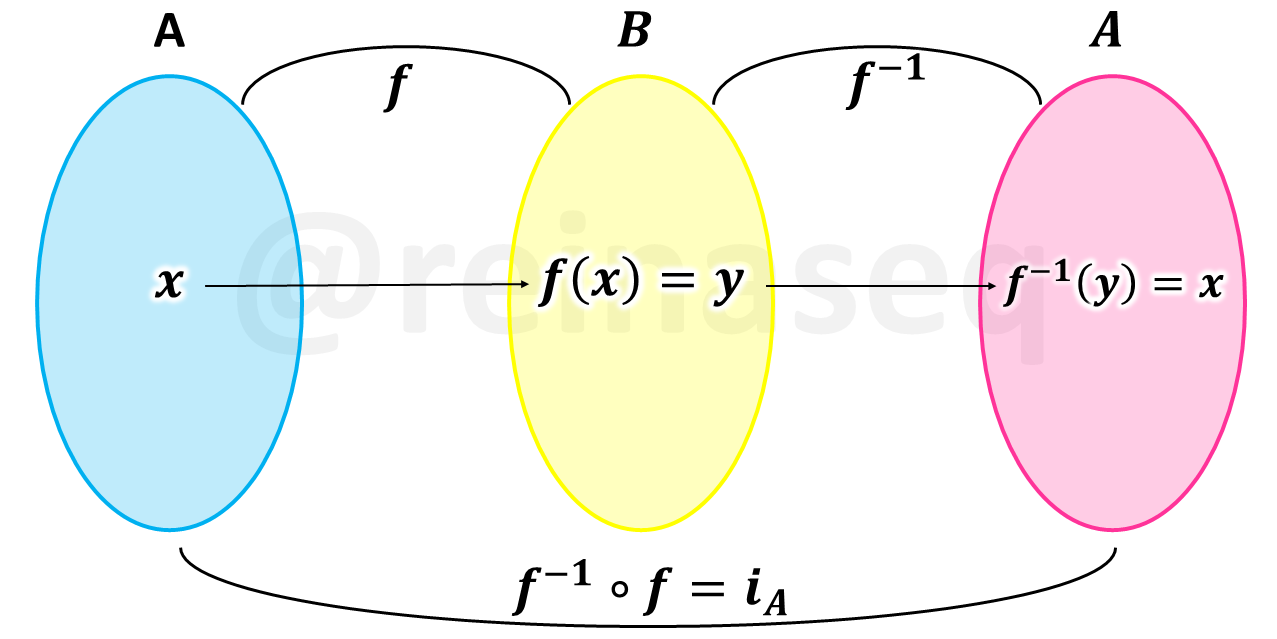
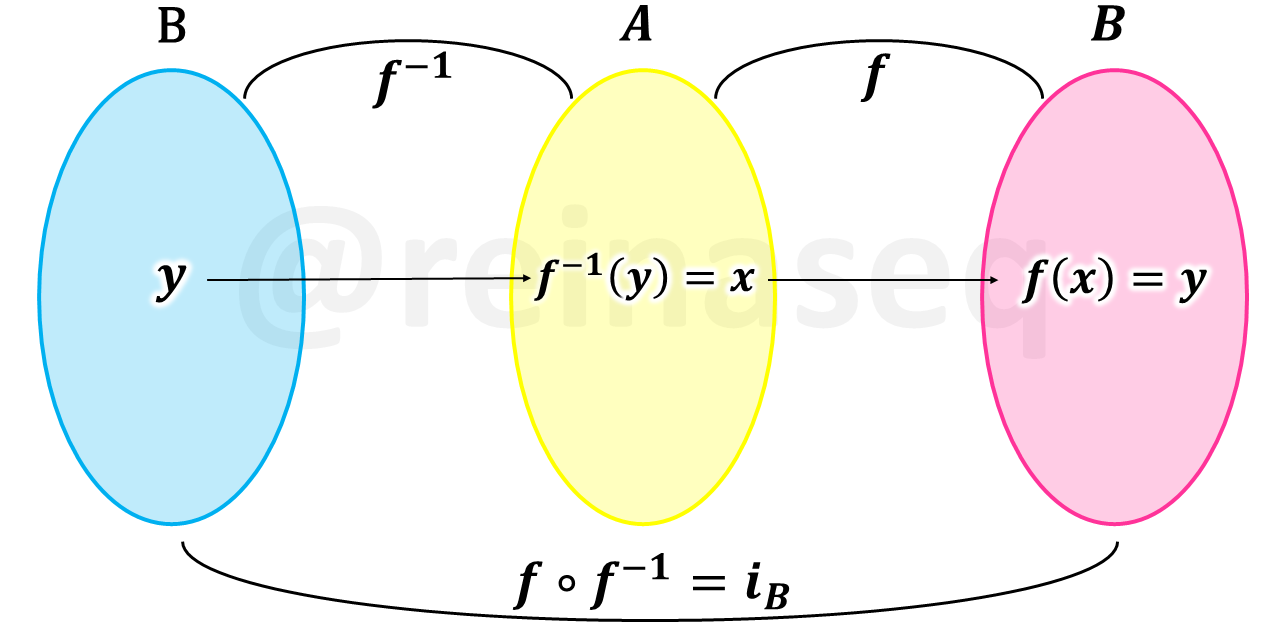
Ahora bien, la *función inversa* de una función *f* cualquiera al graficarla conjuntamente con ésta, genera *gráficos simétricos* como puede observarse y ejemplificarse en los siguientes gráficos cartesianos

![7.PNG](https://cdn.steemitimages.com/DQmd1sKZsyZfJpEzbnSTYt2TcNmgDf3D3H4Badsmh8o1spE/7.PNG)
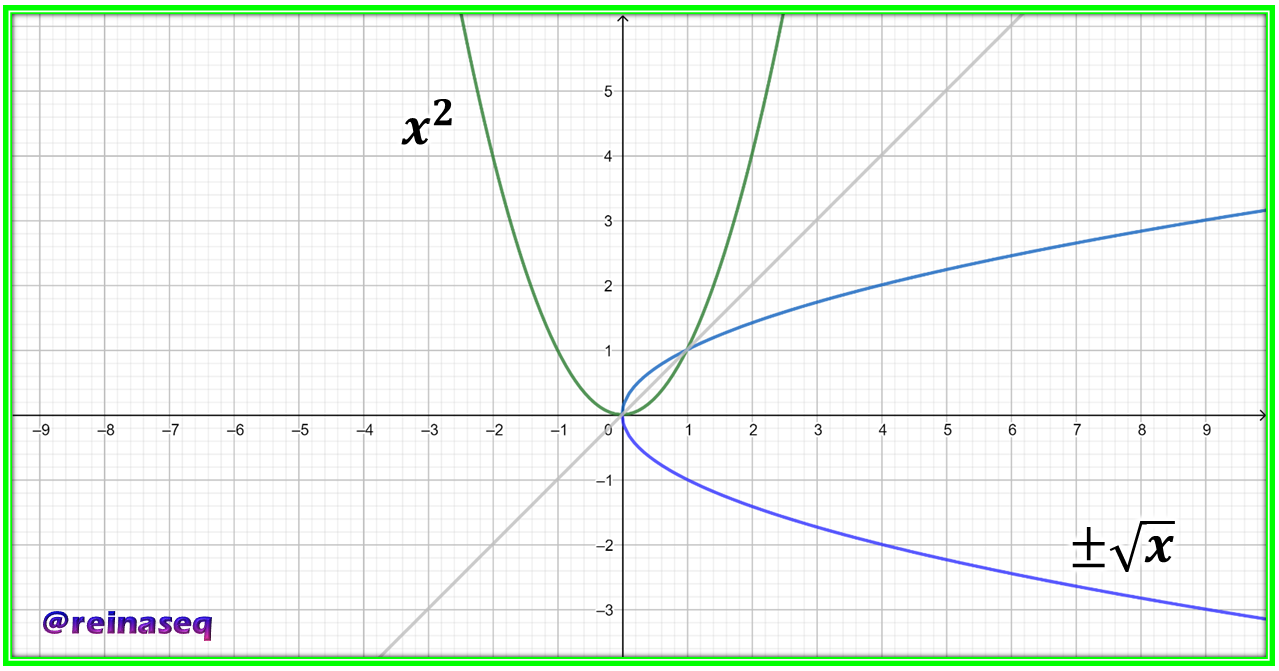
<center><sup>Gráfica de las funciones definidas por *f(x)=x<sup>2</sup>* y *f<sup>-1</sup>(x)=x<sup>1/2</sup>* diseñada por @reinaseq mediante el software [Geogebra en Línea](https://www.geogebra.org/?lang=es) </sup></center>

![8.PNG](https://cdn.steemitimages.com/DQmNeVCfJYXqgmEvXMNtxt5hDgUoHDrdoj6a8H6eWyjDCEK/8.PNG)
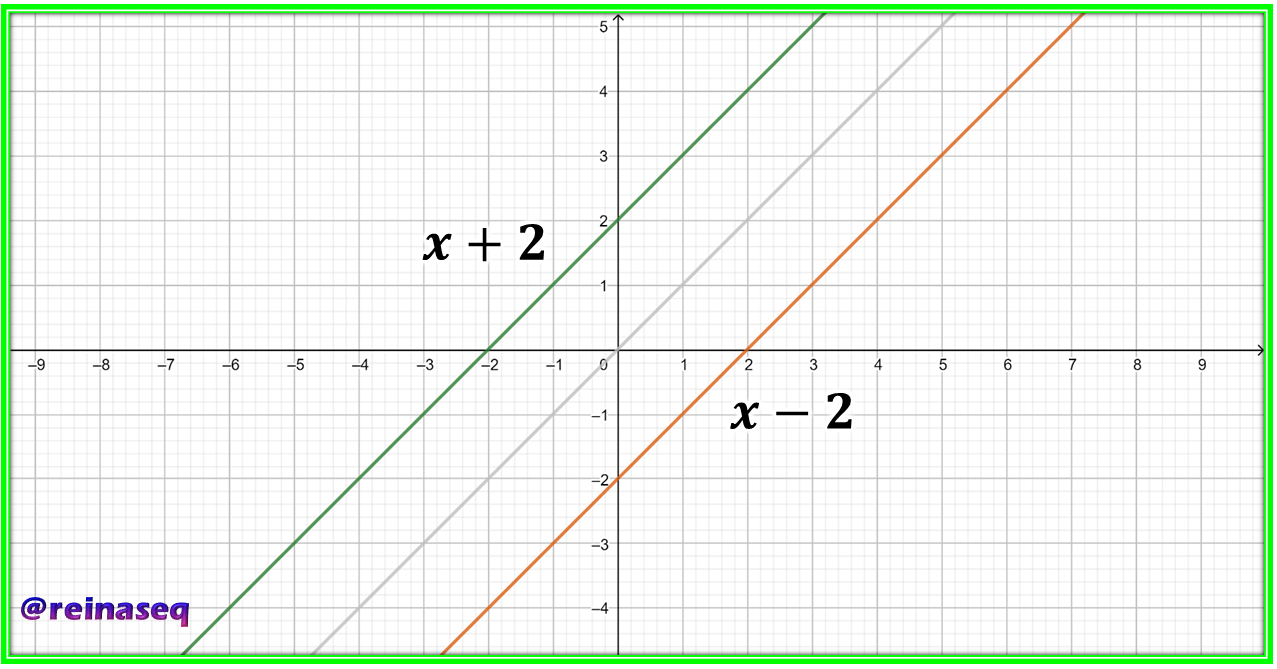
<center><sup> Gráfica de las funciones definidas por *f(x)=x+2* y *f<sup>-1</sup>(x)=x-2* diseñada por @reinaseq mediante el software [Geogebra en Línea](https://www.geogebra.org/?lang=es) </sup></center>

#### <p>**Ejemplo**</p>

Dada la función **f:R⟶R** definida por **f(x)=3x-2**, se pide lo siguiente:
* Determinar **f<sup>-1</sup>**
* Determinar **f<sup>-1</sup>∘f** y **f∘f<sup>-1</sup>**

*Solución*

Antes de pasar al procedimiento matemático, debemos tener presente que toda función definida por la forma **ax+b** se conoce como *función lineal o afín* y la misma es biyectiva. Esta aclaratoria tendrá significado en el siguiente apartado.

Para obtener la *función inversa* solicitada debemos proceder de la siguiente manera:

Si **y=f(x)⟹y=3x-2**, por definición de la función *f*
**⟹y=3x+(-2)**, por convenio de notación *x-x=x+(-x), ∀x∈R*
**⟹y+2=3x+[(-2)+2]**, sumando *2* a derecha en ambos miembros de la igualdad y por propiedad asociativa de la adición en el conjunto de los números reales ***R***
**⟹y+2=3x+0**, por definición de elemento opuesto en el conjunto de los números reales ***R***
**⟹y+2=3x**, por definición de elemento neutro para la adición en el conjunto de los números reales ***R***
**⟹1/3.(y+2)=[(1/3).3]x**, multiplicando *1/3* a izquierda en ambos miembros de la igualdad y por propiedad asociativa de la multiplicación en el conjunto de los números reales ***R***
**⟹1/3.(y+2)=1.x**, por definición de elemento inverso en el conjunto de los números reales ***R***
**⟹1/3.(y+2)=x**, por definición de elemento neutro para la multiplicación en el conjunto de los números reales ***R***
**⟹x=1/3.(y+2)**, por simetría de la igualdad

En este punto, la *variable independiente y* de la *función inversa* **f<sup>-1</sup>** está expresada en función de su *variable dependiente x*, no obstante, por convención se acostumbra en general que las letras que identifican las variables de las funciones se denoten como sigue

* *variable dependiente:* **y**
* *variable independiente:* **x**

Es por ello que en nuestro ejemplo, la expresión que define a **f<sup>-1</sup>** se escribe como sigue

**⟹y=1/3.(x+2)**

Por lo tanto, **f<sup>-1</sup>** es

**f<sup>-1</sup>:R⟶R/f<sup>-1</sup>(x)= 1/3.(x+2)**

Ahora procedemos con la segunda solicitud del problema, es decir; determinar **f<sup>-1</sup>∘f** y **f∘f<sup>-1</sup>**. Procedamos:

**i** **(f<sup>-1</sup>∘f)(x)=f<sup>-1</sup>[f(x)]**, por definición de *función compuesta*
**⟹f<sup>-1</sup>[f(x)]=f<sup>-1</sup>(3x-2)**, por definición de *f*
**⟹f<sup>-1</sup>[f(x)]=1/3.[(3x-2)+2]**, por definición de *f*
**⟹f<sup>-1</sup>[f(x)]=1/3.{[3x+(-2)]+2}**, por convenio de notación *x-x=x+(-x), ∀x∈R*
**⟹f<sup>-1</sup>[f(x)]=1/3.{3x+[(-2)+2]}**, por propiedad asociativa de la adición en el conjunto de los números reales ***R***
**⟹f<sup>-1</sup>[f(x)]=1/3.[3x+0]**, por definición de elemento opuesto en el conjunto de los números reales ***R***
**⟹f<sup>-1</sup>[f(x)]=1/3.(3x)**, por definición de elemento neutro para la adición en el conjunto de los números reales ***R***
**⟹f<sup>-1</sup>[f(x)]=[(1/3).3].x**, por propiedad asociativa de la multiplicación en el conjunto de los números reales ***R***
**⟹f<sup>-1</sup>[f(x)]=1.x**, por definición de elemento inverso en el conjunto de los números reales ***R***
**⟹f<sup>-1</sup>[f(x)]=x**, por definición de elemento neutro para la multiplicación en el conjunto de los números reales ***R***

**∴f<sup>-1</sup>[f(x)]=x**

**∴f<sup>-1</sup>∘f=i<sub>R</sub>**

**ii** **(f∘f<sup>-1</sup>)(x)=f[f<sup>-1</sup>(x)]**, por definición de *función compuesta*

**⟹f[f<sup>-1</sup>(x)]=f[1/3.(x+2)]**, por definición de *f<sup>-1</sup>*
**⟹f[f<sup>-1</sup>(x)]=3.[1/3.(x+2)]-2**, por definición de *f*
**⟹f[f<sup>-1</sup>(x)]=3.[1/3.(x+2)]+(-2)**, por convenio de notación *x-x=x+(-x), ∀x∈R*
**⟹f[f<sup>-1</sup>(x)]=[(3.1/3).(x+2)]+(-2)**, por propiedad asociativa de la multiplicación en el conjunto de los números reales ***R***
**⟹f[f<sup>-1</sup>(x)]=[1.(x+2)]+(-2)**, por definición de elemento inverso en el conjunto de los números reales ***R***
**⟹f[f<sup>-1</sup>(x)]=(x+2)+(-2)**, por definición de elemento neutro para la multiplicación en el conjunto de los números reales ***R***
**⟹f[f<sup>-1</sup>(x)]=x+[2+(-2)]**, por propiedad asociativa de la adición en el conjunto de los números reales ***R***
**⟹f[f<sup>-1</sup>(x)]=x+0**, por definición de elemento opuesto en el conjunto de los números reales ***R***
**⟹f[f<sup>-1</sup>(x)]=x**, por definición de elemento neutro para la adición en el conjunto de los números reales ***R***

**∴f[f<sup>-1</sup>(x)]=x**

**∴f∘f<sup>-1</sup>=i<sub>R</sub>**

A continuación se realiza la representación gráfica de *f* y *f<sup>-1</sup>*

![9.PNG](https://cdn.steemitimages.com/DQmWrEc31nMZvSaR4xa9Wahzn2rSkx2vw8Rghc7823TFYir/9.PNG)
<center><sup> Gráfica de las funciones definidas por *f(x)=3x-2* y *f<sup>-1</sup>(x)=1/3.(x+2)* diseñada por @reinaseq mediante el software [Geogebra en Línea](https://www.geogebra.org/?lang=es) </sup></center>

![3.png](https://cdn.steemitimages.com/DQmPxGLeiiTmjpXjhsChpSqR5Ttja3g3u5Uf2DrFSqA2k2U/3.png)

En el ejemplo anterior tuvimos que indicar *a priori* que la función dada era biyectiva antes de proceder a determinar su *función inversa*, esto era necesario debido al siguiente teorema: 

La función *f:A⟶B* admite *función inversa* *f<sup>-1</sup>:B⟶A* si y sólo si es biyectiva

Antes de realizar la demostración, conviene recordar que en publicación anterior – [ver quí](https://steemit.com/spanish/@reinaseq/funciones-nociones-fundamentales) – se analizó la relación que existe entre *unicidad de imagen* e *inyectividad* y entre *existencia de imagen* y *sobreyectividad* debido a la perspectiva que presentan las mismas que conlleva a que en ocasiones existan confusiones entre unas y otras. 

Ahora bien, supongamos que estamos en el escenario en el cual la función dada no es biyectiva y aun así procedemos a determinar su *función inversa*, entonces como podríamos asegurar que ésta es función, al no ser *f* inyectiva tenemos que *f<sup>-1</sup>* no cumpliría con la condición de *unicidad de imagen* y al no ser *f* sobreyectiva la *función inversa* no cumpliría con la condición de *existencia de imagen*, de allí la importancia del teorema planteado, el cual se procederá a demostrar a continuación:

Por tratarse de una **proposición bicondicional**, tenemos que demostrar dos teoremas implícitos: 

**i** **Teorema Directo:** Si la función *f:A⟶B* admite *función inversa* *f<sup>-1</sup>:B⟶A* entonces es biyectiva

**ii** **Teorema Recíproco:** Si la función *f:A⟶B* es biyectiva entonces admite *función inversa* *f<sup>-1</sup>:B⟶A*

Recordemos que en una **proposición condicional** se cuenta con una hipótesis que apoya el proceso demostrativo y la tesis que representa lo que se va a comprobar.

*Demostrando*

**i** **Teorema Directo:** Si la función *f:A⟶B* admite *función inversa* *f<sup>-1</sup>:B⟶A* entonces es biyectiva

Para esta demostración se considera lo siguiente:

*Hipótesis:* La función *f:A⟶B* admite *función inversa* *f<sup>-1</sup>:B⟶A*, de tal manera que sabemos que se cumple que *f<sup>-1</sup>∘f=i<sub>A</sub>* y *f∘f<sup>-1</sup>=i<sub>B</sub>*

*Tesis:* La función *f:A⟶B* es biyectiva

La demostración solicitada pasa por verificar que *f:A⟶B* es inyectiva, sobreyectiva y biyectiva.

a. *Inyectividad*

**∀a,b∈A;f(a)=f(b)⟹f<sup>-1</sup>[f(a)]=f<sup>-1</sup>[f(b)]**, por hipótesis la función *f:A⟶B* admite *función inversa* *f<sup>-1</sup>*
**⟹(f<sup>-1</sup>∘f)(a)=(f<sup>-1</sup>∘f)(b),** por definición de *función compuesta*
**⟹i<sub>A</sub>(a)=i<sub>A</sub>(b),** por hipótesis que *f<sup>-1</sup>∘f=i<sub>A</sub>*
**⟹a=b,** por definición de *función identidad*
**∴ La función *f:A⟶B* es inyectiva**, por definición de inyectividad

b. *Sobreyectividad*

**∀y∈B⟹y=i<sub>B</sub>(y),** por definición de *función identidad*
**⟹y=f∘f<sup>-1</sup>(y),** por hipótesis *f∘f<sup>-1</sup>=i<sub>B</sub>*
**⟹y=f[f<sup>-1</sup>(y)],** por definición de *función compuesta*

**∴ La función *f:A⟶B* es inyectiva**, por definición de sobreyectividad

**∴ Si la función *f:A⟶B* admite función inversa entonces es biyectiva**, por comprobaciones *a* y *b* y definición de biyectividad

**ii** **Teorema Recíproco:** Si la función *f:A⟶B* es biyectiva entonces admite *función inversa* *f<sup>-1</sup>:B⟶A*

*Tesis:* La función *f:A⟶B* es biyectiva (inyectiva y sobreyectiva)

*Hipótesis:* La función *f:A⟶B* admite *función inversa* *f<sup>-1</sup>:B⟶A*, de tal manera que *f<sup>-1</sup>∘f=i<sub>A</sub>* y *f∘f<sup>-1</sup>=i<sub>B</sub>*

a. En primer lugar se debe definir una función que pueda verificar las demás proposiciones planteadas en la tesis, esto es 

**∃f<sup>-1</sup>:B⟶A** definida por **x=f<sup>-1</sup>(y)** si y sólo si **y=f(x)** **(I)**

Ahora se debe comprobar que efectivamente **f<sup>-1</sup>** cumple con las condiciones de *existencia de imagen* y *unicidad de imagen*. Procedamos:

*Existencia de Imagen*

Como por hipótesis tenemos que *f:A⟶B* es biyectiva, esto indica que la misma es sobreyectiva, esto indica que todo elemento del conjunto ***B*** tiene su preimagen en el conjunto ***A***, de tal manera que al tener un escenario en el cual se define **f<sup>-1</sup>:B⟶A** mediante **x=f<sup>-1</sup>(y)** donde **y=f(x)**, es claro que se cumple que

**∀y∈B,∃x∈A/x=f<sup>-1</sup>(y)**

**∴ f<sup>-1</sup> cumple con la condición de existencia de imagen**

*Unicidad de Imagen*

Como en el razonamiento anterior, tenemos por hipótesis que *f:A⟶B* es biyectiva, por lo cual es inyectiva, esto nos indica que en **f<sup>-1</sup>:B⟶A** definida como está garantizado que para elementos iguales en el *conjunto de partida B* sus imágenes son iguales en el *conjunto de llegada A*, en símbolos

**∀a,b∈B/a =b⟹f(a)=f(b)**

**∴f<sup>-1</sup> cumple con la condición de unicidad de imagen**
**∴f<sup>-1</sup> es función**

A continuación procedemos a demostrar las dos proposiciones restantes de la tesis.

b. Comprobemos que *f<sup>-1</sup>∘f=i<sub>A</sub>*

**∀x∈A,(f<sup>-1</sup>∘f)(x)=f<sup>-1</sup>[f(x)],** por definición de función compuesta
**=f<sup>-1</sup>(y),** por definición **I**
**=x,** por definición **I**
**=i<sub>A</sub>(x),** por definición de *función identidad*

**∴f<sup>-1</sup>∘f=i<sub>A</sub>**

c. Comprobemos que *f∘f<sup>-1</sup>=i<sub>B</sub>*

**∀y∈B,(f∘f<sup>-1</sup>)(y)=f[f<sup>-1</sup>(y)],** por definición de función compuesta
**=f(x),** por definición **I**
**=y,** por definición **I**
**=i<sub>B</sub>(x),** por definición de *función identidad*

**∴f∘f<sup>-1</sup>=i<sub>B</sub>**

**∴ Si la función *f:A⟶B* es biyectiva entonces admite función inversa**, por comprobaciones *a*, *b* y *c*.

**∴ La función *f:A⟶B* admite función inversa si y sólo si es biyectiva**∎

![4.png](https://cdn.steemitimages.com/DQmeUVpK7JwkTCxNWciSfyhbsPGDPr3egHh1sofJkNZADoW/4.png)

La aplicabilidad de la *función inversa* en general se encuentra estrechamente vinculada con el ámbito de aplicación de las funciones en general, en tanto que la misma deriva de una función *f:A⟶B* cualquiera. En este sentido mencionamos a continuación algunas posibilidades:

* Permiten determinar relaciones entre magnitudes en la Física, Química, Economía, entre otras.
* Son utilizadas en los estudios de proporcionalidad, tasas de variación y para realizar predicciones en cuanto a ganancias y pérdida.
* Se usan en el estudio de trayectorias, apoyan el estudio de lanzamientos de proyectil.
* Se puede estudiar la relación existente entre la cantidad de pacientes atendidos en una consulta en función del tiempo de atención que reciben.
* Permiten estudiar el crecimiento poblacional (seres humanos, animales, bacterias, virus), así como la desintegración radioactiva.
* Son utilizadas en geología para el estudio de los sismos.
* Se usan en el diseño de planos y en el cálculo de resistencia de materiales.
* En Astronomía se utilizan en el cálculo de la órbitas de los planetas y la determinación de magnitudes estelares.

Las mencionadas son apenas algunas oportunidades de aplicación de las *funciones inversas*, en general ya se había indicado en publicaciones anteriores que las *funciones* por su naturaleza son consideradas un concepto medular en el ámbito de la Matemática por la diversidad de aplicaciones que la misma tiene. Para ejemplificar de forma concreta la aplicación de la *función inversa* se plantea la resolución del siguiente problema:

* **Ejemplo**

Dada la función **f:R⟶R** definida por **f(°C)=9/5°C+32** que permite transformar grados *Celsius* a grados *Fahrenheit* se pide determinar su *función inversa* **f<sup>-1</sup>** que permitirá transformar grados *Fahrenheit* a grados *Celsius* y graficar ambas.

*Solución*

Para determinar **f<sup>-1</sup>** procedemos como sigue

Si **°F=9/5°C+32⟹°F+(-32)=9/5°C+[32+(-32)]**, sumando (-32) en ambos miembros de la igualdad y por propiedad asociativa de la adición en el conjunto de los números reales ***R***
**⟹°F+(-32)=9/5°C+0**, por definición de elemento opuesto en el conjunto de los números reales ***R***
**⟹°F+(-32)=9/5°C**, por definición de elemento neutro para la adición en el conjunto de los números reales ***R***
**⟹5/9.[°F+(-32)]=(5/9.9/5)°C**, multiplicando 5/9 en ambos miembros de la igualdad y por propiedad asociativa de la multiplicación en el conjunto de los números reales ***R***
**⟹5/9.[°F+(-32)]=1.°C**, por definición de elemento inverso en el conjunto de los números reales ***R***
**⟹5/9.[°F+(-32)]=°C**, por definición de elemento neutro para la multiplicación en el conjunto de los números reales ***R***
**⟹°C=5/9.[°F+(-32)]**, por simetría de la igualdad
**⟹°C=5/9.(°F-32)**, por convenio de notación *x-x=x+(-x), ∀x∈R*

**∴ La función inversa f<sup>-1</sup>(°F)=5/9.(°F-32)**

Graficando **f** y **f<sup>-1</sup>** tenemos

![10.PNG](https://cdn.steemitimages.com/DQmcm1RHhjHcFQ9KWVAVpivXFQ9Rwcjv82Svo6FQBPZYGGj/10.PNG)
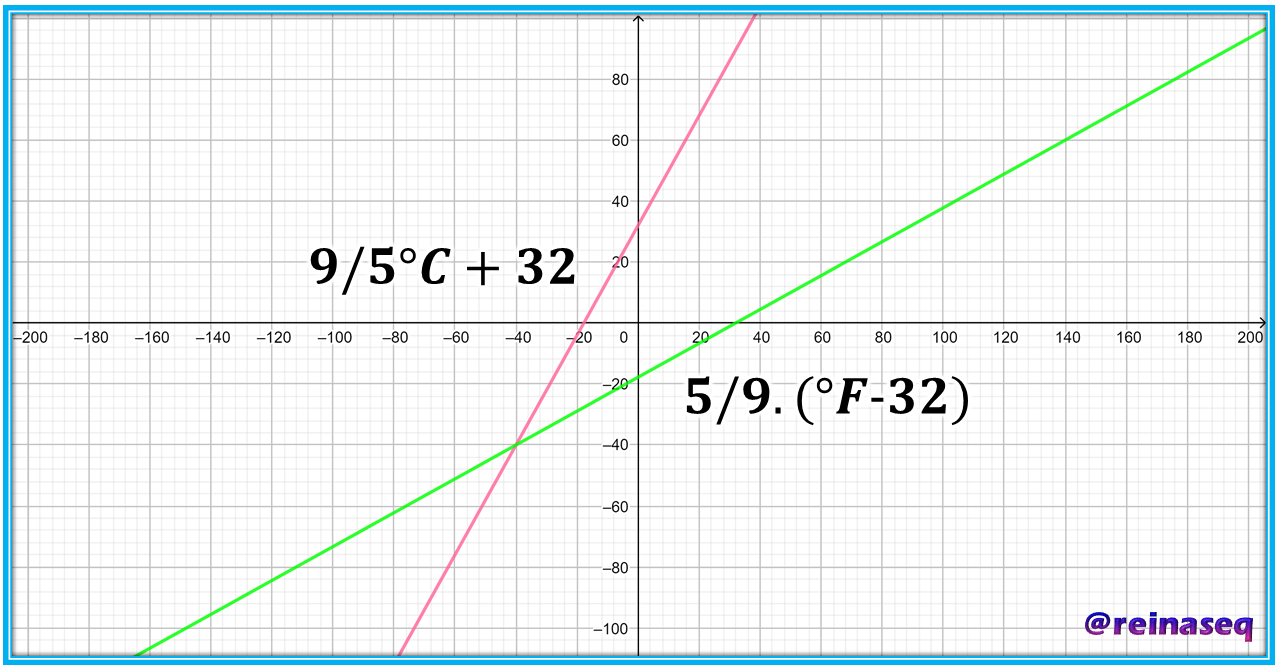
<center><sup> Gráfica de las funciones definidas por *f(°C)=9/5°C+32* y *f<sup>-1</sup>(°F)=5/9.(°F-32)* diseñada por @reinaseq mediante el software [Geogebra en Línea](https://www.geogebra.org/?lang=es) </sup></center>

![5.PNG](https://cdn.steemitimages.com/DQmSnQBMzjp4UinvWREWXHZTSRoNAxpxaq6EXZZpDLd1AnW/5.PNG)

En esta oportunidad hemos dado realizado un estudio detallado y exhaustivo sobre la *función inversa*, desde las perspectivas algebraica, gráfica y práctica, presentando un breve arqueo de sus ámbitos de aplicación y desarrollando ejercicios que permiten comprender de forma concreta esta importante noción, es importante destacar la demostración del teorema relativo a la posibilidad de que una función cualquiera pueda **admitir** su respectiva *función inversa* y es que si la misma no cumple con la biyectividad no se puede garantizar que la inversa sea función, en tanto que podría no verificar algunas o ambas condiciones para que así sea, a saber, *existencia de imagen* y *unicidad de imagen*, todo dependiendo de los motivos por los cuales la función no sea biyectiva.

En Matemática, las definiciones, propiedades y teoremas que la sustentan y la hacen crecer, no están dados por capricho, cada una tiene su sustentabilidad teórica que las respalda, de allí que la misma siga impulsando avances para el progreso y evolución de la humanidad, de allí la preocupación por presentar en cada entrega las diferentes concepciones matemáticas con el detalle y especificidad que amerita para así entender cada una de las piezas que conforman esta importante ciencia. Si queremos que la juventud se incline hacia el estudio científico es vital que tengan acceso a materiales de estudio que les brinden claridad.

En las próximas publicaciones, seguiremos avanzando en el estudio de las **funciones** abordando un nuevo tópico, nos leemos en el siguiente post, saludos y éxitos para todos los lectores y académicos de esta comunidad.

![3.png](https://cdn.steemitimages.com/DQmUeSpapihbuoKMj9pA6rP387mXzbZXFPyapuFkpVg9FqP/3.png)
### <center> <p>La Matemática debe ser presentada con el mayor detalle y especificidad en sus procesos para facilitar la comprensión de las nuevas generaciones de científicos – Reina Sequera </p></center>
![3.png](https://cdn.steemitimages.com/DQmUeSpapihbuoKMj9pA6rP387mXzbZXFPyapuFkpVg9FqP/3.png)

### **Referencia**

Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Becerril, R. y Reyes, J. (2012). Precálculo. México: Trillas.
Lipschutz, S. (1970). Teoría de Conjuntos y Temas Afines. Teoría y 530 problemas resueltos. Serie de compendios SCHAUM. Mc Graw-Hill.

**Páginas Consultadas:** [1](https://prezi.com/tbqkv_yg3ara/aplicaciones-de-las-funciones-en-la-vida-cotidiana/) y [2](http://entenderlasmates.blogspot.com/2016/09/las-funciones-en-la-vida-cotidiana-1.html)

**Todas las imágenes, separadores y banners de este artículo son de autoría propia diseñadas en el editor de presentaciones *Microsoft Powerpoint 2013*, ajustadas y recortadas en *Paint*.**

**Los gráficos cartesianos fueron diseñados por @reinaseq mediante el software [Geogebra en Línea](https://www.geogebra.org/?lang=es)**

---

### **Publicaciones Relacionadas**

* [Funciones: Nociones Fundamentales](https://steemit.com/spanish/@reinaseq/construccion-del-conjunto-de-los-numeros-enteros-z)
* [Composición de Funciones](https://steemit.com/spanish/@reinaseq/composicion-de-funciones)

---

#### <center><p>Si estás interesado en contenidos sobre Ciencia, Tecnología, Ingeniería y Matemática, consulta las etiquetas #STEM-Espanol y #SteemSTEM, las cuales puedes utilizar para realizar tus publicaciones en esas áreas. Puedes unirte al servidor de Discord de STEM-Espanol para participar en nuestra comunidad y consultar los reportes semanales publicados por @STEM-Espanol. Te esperamos!!</p></center>

* [Normas STEM-Espanol](https://steemit.com/stem-espanol/@stem-espanol/presentacion-stem-espanol)
* [Directrices sobre normas de derechos de autor](https://steemit.com/stem-espanol/@carloserp-2000/directrices-sobre-normas-de-derechos-de-autor-en-steemstem-stem-espanol)
* [Servidor Discord #STEM-Espanol](https://discordapp.com/invite/a2yazbz)
* [Para unirte al trail de STEM-Espanol](https://steemit.com/stem-espanol/@stem-espanol/unete-a-trail-stem-espanol)
* [Vota por  @stem.witness como Testigo aquí](https://steemit.com/~witnesses)

<center>![stem_es.png](https://cdn.steemitimages.com/DQmc6Kc7wxzrNu8ESuFDgFTABBRv9pAQxQKMupDZrKiTgdR/stem_es.png)</center>
<center><sup>Créditos: @stem-espanol</sup></center>

</div>

![2.png](https://cdn.steemitimages.com/DQmeDTD3xhj94H1r8VfhHW7Qe1eAaMZekTX54So5s5s7HhG/2.png)

![1.png](https://cdn.steemitimages.com/DQmTwjXurMhXdkrhgcbdPyP8yLCW64YRGiKh5Sv6KbuT4iA/1.png)