안녕하세요? ryanhan입니다!
오늘은 확률에 대하여 이야기해보려고 합니다.
여러분들은 확률 계산을 좋아하시나요? 저는 좋아합니다.
확률을 계산해보고 결과를 예측해보는 일은 재미있습니다.
(또, 투자에서도 중요한 것 같습니다)
그럼 확률에 대해서 이야기해보겠습니다.

# #1 확률의 고전적 정의
여러분들은 확률의 정의를 어떻게 알고 계신가요?
확률의 고전적정의는 라플라스가 제안하였고, 다음과 같습니다.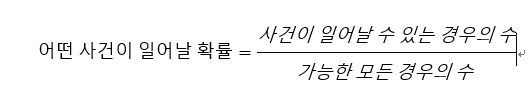
![asdsadqweqwe.png](https://steemitimages.com/DQmbao23ds7bPRPAVop24EebJm655UB9aEYDdZEm4bj4jva/asdsadqweqwe.png)

예를 들어보면,
주사위를 굴려서 3이 나올 확률은
주사위를 굴려서 3이 나올 경우의 수를 
주사위를 굴려서 나올 수 있는 모든 경우의 수로 나누어서 구할 수 있습니다 1/6 이죠!

혹시 이런 확률의 고전적 정의에 의문을 갖고 계셨던 분 있나요??
베르트랑은 이 고전적 정의에 문제가 있단 걸 느끼고
베르트랑의 역설로 불리는 문제를 제시하였습니다.

# #2 베르트랑의 역설
베르트랑의 역설 문제는 다음과 같습니다.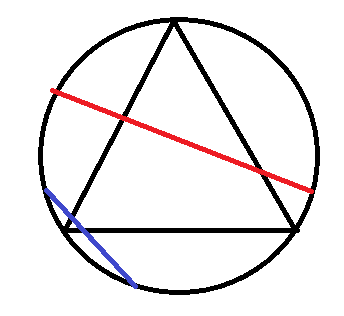

![dasdasd.png](https://steemitimages.com/DQmc8e7tbHi9P6N31v6HiTekC95YJ8PexS4fciYBb8rN65g/dasdasd.png)
**원에 내접하는 정삼각형을 그리고, 원에서 임의의 현을 선택할 때  
그 현의 길이가 정삼각형의 한 변의 길이보다 클 확률은?**
그림에서의 **빨간색 현**처럼 길이가 큰 것이 선택될 확률을 구하면 됩니다.
잠깐 생각해보세요! 
**어떤 방식으로 전체 경우의 수와, 사건의 경우의 수를 구할 수 있을 까요?**

베르트랑은 세 가지 해법을 제시합니다.

# #3 - 1  점 하나를 고정하고, 다른 점을 랜덤 선택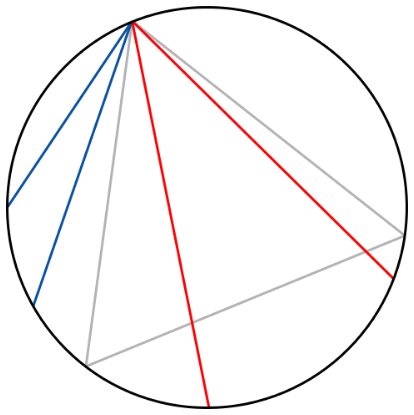
![제목 없음.png](https://steemitimages.com/DQmVnY2DhHPkq7ALv2WiprJbk7QyjvEvVMHQaxAxJcjqGKZ/%EC%A0%9C%EB%AA%A9%20%EC%97%86%EC%9D%8C.png)
현을 이루는 두 점중 하나를 삼각형의 꼭짓점이라하고,
나머지 점을 임의로 선택하는 방법입니다.
정삼각형에 의해 원은 세 등분 되는데요, 
그 중에서 가까운 두 부분에 나머지 점이 선택된다면, 그길이는 삼각형의 변보다 짧습니다.
그리고 먼 부분에 나머지 점이 선택된다면, 그 길이는 삼각형의 변보다 깁니다.
따라서 그 비율을 생각해봤을 때, 전체 경우의 수가 3이라면, 현이 길 경우가 1이므로
### 삼각형의 변보다 길이가 긴 현이 선택될 확률은 1/3입니다!

# #3 - 2 원의 중심과 현사이의 거리를 생각하는 방법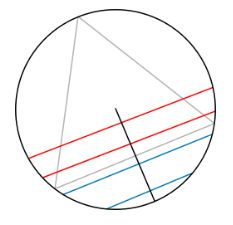

![asdasd.png](https://steemitimages.com/DQmeeawurDYECUGT9SMm4HAAGjx9ieXxmrLbwXij2oL7ECE/asdasd.png)
두 번째 방법은,원의 중심과 현사이의 거리에 따라 분류하는 방법입니다.
이 때, 평행한 현들끼리만 경우의수를 세어도 문제가 없습니다.
이 경우에는 중심과 현 사이의 길이가 가장 작을 때는 그 길이가 0이고, 
이 때 현의 길이가 가장 깁니다.
이 때부터 시작하여 삼각형의 변의 길이와 같은 길이의 현이 선택될 때까지가
우리가 구하고 싶은 경우의 수입니다.
기하학에서 원의 성질에 의하면, 원의 중심과 삼각형의 변까지의 거리는 반지름의 절반입니다.
따라서 전체 경우의 수가 0 ~ 반지름 이고, 
사건의 경우의 수가 0~반지름의 절반 이므로
### 삼각형의 변보다 길이가 긴 현이 선택될 확률은 1/2 입니다!!

# #3 - 3 현의 중점을 생각하는 방법.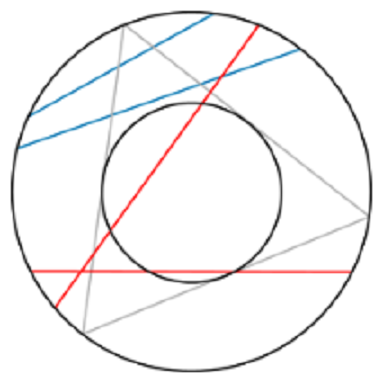

![dsadqwe.png](https://steemitimages.com/DQmR8sKed1aikX2ysLVPmxfRzfntX9NYuvK5L1wzVotZoQL/dsadqwe.png)
원에서는 어떤 현의 중점만 주어지면, 그 현이 어떤 현인지 알 수 있습니다.
따라서, 원 내부에 임의로 현의 중점이 있을 수 있는 것을 전체 경우의 수라하면,
현의 중심이 **내접삼각형의 내접원** 안에 있는 것이 사건의 일어날 경우의 수입니다!
이 때는 원래의 원의 넓이에 비해, 내접삼각형의 내접원의 넓이가 1/4이므로

### 삼각형의 변보다 길이가 긴 현이 선택될 확률은 1/4 입니다!!

# #4 결론
여러분은 세 가지 방법 중 어떤 것을 생각하셨나요??

세 가지 방법은 결과가 모두 달랐습니다.

하지만 세 가지 방법 모두 나름대로의 논리가 있습니다.

어떤 것은 맞고 어떤 것은 틀리다고 할 수 있을까요?

확률의 고전적 정의에서는 세가지 모두 맞는 것 처럼 보입니다.

어쩌면 우리는 확률의 정의부터 다시 배워야 할지도 모르겠습니다.

베르트랑의 역설, 흥미로우셨나요??

다음에도 재미있는 내용으로 포스팅해보겠습니다!

감사합니다. ryanhan이었습니다.