# What the many-body problem is about
<hr>

All many-body problems have two essential ingredients. 
1.	There have to be many bodies present (obviously) e.g. many electrons, many atoms, many molecules, many people etc.
<center>![](https://steemitimages.com/DQmS3gXnYvzFfjD1EEf5MEFJm5iF1NMBLSSVXGtBXsnbXF7/image.png)</center>

2.	For there to be a problem, these bodies have to interact with each other. If the interactions of the bodies are independent of each other, we would simply then have to example each body separately. 

**Many body problems’** importance is based on the fact that real physical systems are composed of a set of interacting particles. e.g. nucleons in a nucleus interact by nuclear forces, electrons in an atom interact by Coulombs forces.

The calculation of physical properties of such systems (e.g. *magnetic susceptibility, energy levels of the atoms*) is based on the interactions between particles of the system. 

The many-body problem involves very intricate motions of the particles in an interacting system. Because of this complexity, scientists before simply prefer a method by pretending the interactions does not exist. Fortunately, this ‘method’ produced good approximate results making a little progress along the way.

The figure below shows the intricate motions of interacting particles contrasted with the simple motions of non-interacting particles. 

<center>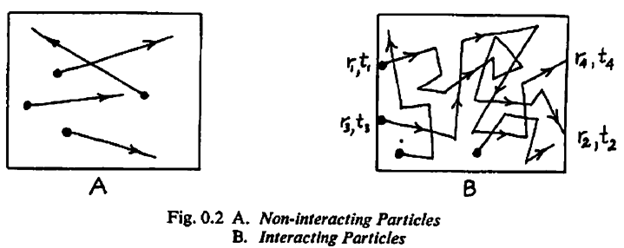![](https://steemitimages.com/DQmPXCFvUTa1svcKVFhEC3ebgdzxEH4FNpD898U6fGPJZgy/image.png)
</center>

Another early approaches to the many-body problem is the [**canonical transformation technique**](https://en.wikipedia.org/wiki/Canonical_transformation). This method involves a new set of coordinates which has smaller number of interacting terms after some basic transformation of the many-body problem. 

However, it was not systematic enough leaving the many-body fields in its cradle into the 1950s.

Around 1956 to 1957, in a series of pioneering papers, [**quantum field theory**](https://en.wikipedia.org/wiki/Quantum_field_theory) provided a new way of attacking the many-body problem.  The idea was then applied to nuclei, electrons in metals, ferromagnets, atoms, superconductors, plasmas, molecules and others. 

Quantum field theory fundamental research is most exciting field from that time on. In line with this development, a new perspective of matter was emerging. Systems of interacting particles are described in terms of approximate non-interacting fictitious bodies called **‘quasi particles’** and **‘collective excitations’**. In addition to that, validations of the results of the calculated physical quantities using quantum field theory were in excellent agreement.

In the incoming series of the guide to to Feynman Diagrams in the many-body problem, we will try to answer the following objectives:

## Objectives:
- **we will give a physical picture of quasi particles and collective excitation** 
- **describe quasi particles and calculate their properties by means of the quantum field theoretical technique known as the method of** **Feynman diagrams**.

# Simple example of non-interacting fictitious bodies
The system is composed of strongly interacting real bodies’ acts as if it were composed of weakly interacting fictitious bodies. 

# Quasi particles and quasi horses
<hr> 

## ‘Quasi particles’

Quasi particles arise from the fact that when real particle moves through the system, it pushes or pulls on its neighbours and thus becomes surrounded by ‘cloud’ of agitated particles similar to the dust cloud kicked up by a galloping horse.

**Quasi particle is the real particle plus its cloud.** 
<center>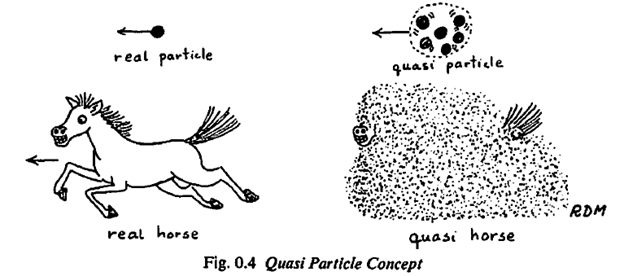![](https://steemitimages.com/DQmYDcF3vrJKuMhobqLx2vhjKfexMzFCKc9UiPL5Lnusrvh/image.png)</center> 

Just as the dust cloud hides the horse, the particle cloud ‘shields’ or ‘screen’ the real particles so that the quasi-particles interact weakly with one another. This presence of the cloud introduces an additional mass to the real particle so we have an ‘effective mass’ different from the real mass, and a ‘lifetime’. All of these properties are observed experimentally. 

Note, however, that the quasi particle is in an excited energy level of the many-body system, hence it is also referred to as an ‘elementary excitation’ of the system. 

#### Examples of quasi particles:
1.	Quasi ions in a classical liquid
2.	Quantum system: quasi electron in electron gas
3.	Single electron in a metal
4.	Quasi nucleon
5.	Bogoliubov quasi particles (‘bogolons’)

# Collective excitations
<hr> 

There are some fictitious particles in many body problems that do not centre around individual particles like quasi particle but instead involve collective, wavelike motion of all the particles in the system simultaneously. These fictitious particles are called ‘collective excitations’.

Some examples of collective excitations:
1.	Plasmons: are collective (a discrete number) oscillations of the free electron gas density.
2.	Phonons: a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, like solids and some liquids.
3.	Magnons: a collective excitation’s of the electron’s spin structure in a crystal lattice
4.	Nuclear quanta: a collective excitations of the vibrational and rotational motions in a nuclei

Next, we’re going to discuss in a qualitative way how to find the properties of quasiparticles and collective excitations using **propagators and Feynman diagrams.**


<br>
<br>
<sup>Disclaimer: this is a summary of chapter 0 from the book A Guide to Feynman Diagrams: by Richard D. Mattuck, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.</sup>

1. [A Guide to Feynman Diagrams in the Many-Body Problem](https://github.com/valjen/book_collection/tree/master/Physics/A%20Guide%20to%20Feynman%20Diagrams)

<hr>

<center> Thank you for reading ...
![](https://steemit-production-imageproxy-upload.s3.amazonaws.com/DQmeJgsbM5K3pUC8kPBToDKRxE2gijUXvgvX6oUiBgaaiyk)
![](https://steemitimages.com/DQmNXXLQdbXpB1WuRn2YErhQLznZVCdUW3kc7sutPWxA8vv/image.png)
</center>