![image.png](https://images.hive.blog/DQmVDfGXPHRswyXKr8AY7ktJUeJNkf2ZQQD2AHo3QUfBJiX/image.png)

To determine whether an electronic device can be used in space, engineers must assess its susceptibility to radiation. Understanding how radiation affects electronic components is crucial for designing protective measures and ensuring reliable software execution. This article explores key parameters used to describe radiation effects on electronic circuits.

---

## Description of the Radiation Environment

Space radiation consists of various high-energy particles originating from different sources, each carrying different levels of energy. To characterize this radiation, scientists use models that describe particle flux and energy distribution.

### Flux and Fluence of Particles

- **Flux** is a measure of how densely an area is filled with moving particles. Imagine placing a square frame in space and counting the particles passing through it. Flux is defined as the number of particles crossing a unit area per second and is typically expressed in units of:

  \[
  \frac{1}{s \cdot cm^2}
  \]

- **Fluence** represents the total number of particles that pass through a given area over a specific period of time. It is measured in:

  \[
  \frac{1}{cm^2}
  \]

---

## Resistance to Total Ionizing Dose (TID)

When exposed to radiation, semiconductors absorb energy, potentially leading to permanent damage. The **Total Ionizing Dose (TID)** is defined as the energy absorbed per unit mass of material during exposure to radiation. The most common unit of measurement is the rad:

\[
1 \text{ rad} = 0.01 \text{ Gy} = 0.01 \frac{J}{kg} = 100 \text{ erg/g}
\]

At a certain TID threshold, a device may experience irreversible failure.

---

## Linear Energy Transfer (LET)

When a heavy ion penetrates an electronic component, it loses energy due to ionization, which can disrupt the material's atomic structure. The **Linear Energy Transfer (LET)** describes the rate at which a particle loses energy as it moves through a medium:

\[
LET = \frac{\Delta E}{\Delta x} \quad [N]
\]

However, expressing LET in **Newtons (N)** is impractical for radiation analysis. Instead, it is more commonly measured in **MeV·cm²/mg** to better represent energy loss in semiconductors. The formula can be rewritten using density (\(\sigma\)):

\[
LET = \frac{E}{S} = \frac{E}{m} \cdot \sigma  \quad \left[\frac{MeV \cdot cm^2}{mg}\right]
\]

Higher LET values indicate that a material effectively stops radiation particles, but this can also lead to greater damage due to higher absorbed energy.

---

## Cross-Section: Measuring Device Susceptibility to Radiation

The **cross-section** is a fundamental parameter used to quantify a device's sensitivity to radiation. It is defined as the ratio of the probability of an event occurring to the particle fluence:

\[
\sigma = \frac{P}{\Phi} \quad \left[cm^2\right]
\]

### SEU Cross-Section
For digital devices, the **Single Event Upset (SEU) cross-section** describes how susceptible memory cells are to radiation-induced bit flips. It is calculated by dividing the number of affected bits by the fluence:

\[
\sigma_{SEU} = \frac{\text{Number of bit errors}}{\text{Fluence}}
\]

If the number of bits in a device is known, the **per-bit SEU cross-section** can also be computed.

Since different particles interact with materials in unique ways, separate cross-section measurements are required for various radiation types, such as **neutrons** and **protons** (especially for energies below 50 MeV).

---

## LET Threshold: Identifying Radiation Sensitivity

During radiation testing, electronic components are exposed to varying particle fluxes to measure SEU cross-sections. The **LET threshold (\(LET_t\))** is the minimum LET value at which the first errors occur. Below this level, the device remains unaffected.

### Example: SEU Cross-Section vs. LET
The graph below compares SEU cross-sections for Motorola PowerPC 7455 at different core voltages:

![image.png](https://images.hive.blog/DQmZ3p6RwyrNUFhwNtxiBqH8Vg8MV1uh9Tp7jEdStY2fCzg/image.png)


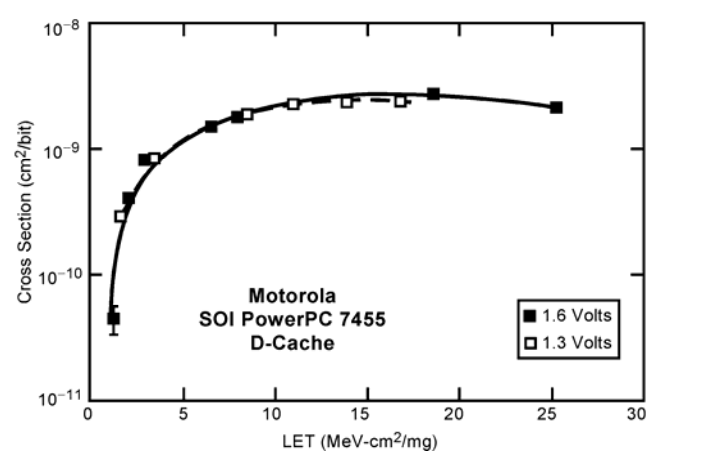
For **low LET values**, the SEU cross-section is nearly zero, meaning the device is resistant to radiation. However, as LET increases, the number of errors rises sharply. Understanding this behavior allows engineers to evaluate radiation-hardening techniques.

---

## Final Thoughts

Space radiation presents a significant challenge for electronic circuits used in spacecraft. Engineers rely on parameters such as **flux, fluence, LET, TID, and cross-sections** to evaluate a device's resistance to radiation effects. These metrics help in selecting and designing components that can operate reliably in harsh space environments.

---

## References

1. **Hanslmeier, Arnold** (2004). *The Sun and Space Weather*. Kluwer Academic Publisher, New York.
2. **Mengfei Yang, Gengxin Hua, Yanjun Feng, Jian Gong** (2017). *Fault-Tolerance Techniques for Spacecraft Control Computers*. Wiley.
3. **Peter Fortescue, Graham Swinerd, John Stark** (2011). *Spacecraft Systems Engineering, 4th Edition*. Wiley.
4. **Dodd, P. E., & Massengill, L. W.** (2003). *Basic mechanisms and modeling of single-event upset in digital microelectronics*. IEEE Transactions on Nuclear Science, 50(3), 583-602.
5. **Messenger, G. C., & Ash, M. S.** (1997). *Single Event Phenomena in Microelectronics*. New York: Wiley-Interscience.
6. **Xapsos, M. A., Summers, G. P., Barth, J. L., Stassinopoulos, E. G., & Burke, E. A.** (2000). *Probability model for cumulative solar proton event fluences*. IEEE Transactions on Nuclear Science, 47(3), 486-490.
7. **Barnaby, H. J.** (2006). *Total ionizing dose effects in modern integrated circuits*. IEEE Transactions on Nuclear Science, 53(6), 3103-3121.
8. **Holman, G. D.** (2012). *Solar flares and particle acceleration*. In *The Sun, the Solar Wind, and the Heliosphere* (pp. 141-155). Springer.