04-11-2024 - Analytic Geometry - Matrix Multiplication Example [EN]-[IT]
hive-146620·@stefano.massari·
0.000 HBD04-11-2024 - Analytic Geometry - Matrix Multiplication Example [EN]-[IT]
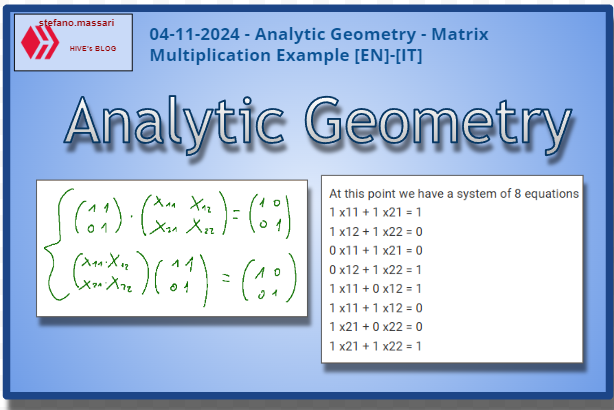 --- *~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~* --- **ENGLISH** **04-11-2024 - Analytic Geometry - Matrix Multiplication Example [EN]-[IT]** With this post I would like to give a brief instruction regarding the topic mentioned in the subject (code notes: X_086) ***Matrix Multiplication Example*** Let's proceed with the multiplication between the following matrices 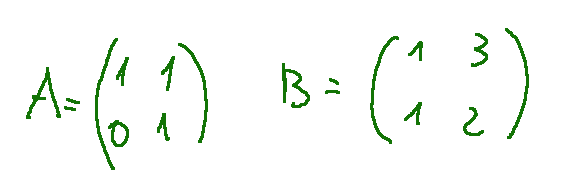 The result for us will be the matrix C which will have the following terms as result c11=a11⋅b11+a12⋅b21 c12=a11⋅b12+a12⋅b22 c21=a21⋅b11+a22⋅b21 c22=a21⋅b12+a22⋅b22 Let's replace the terms c11=1⋅1+1⋅2 c12=1⋅3+1⋅2 c21=0⋅1+1⋅1 c22=0⋅3+1⋅2 We will obtain the following results c11=1⋅1+1⋅2 = 1 + 2 = 3 c12=1⋅3+1⋅2 = 3 + 2 = 5 c21=0⋅1+1⋅1 = 0 + 1 = 1 c22=0⋅3+1⋅2 = 0 + 2 = 2 So the resulting matrix will be the following 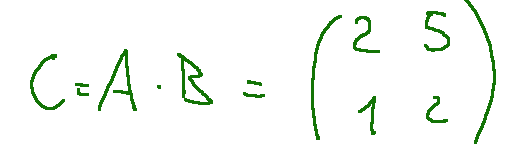 **Inverse matrix** Let's try to find the inverse matrix of 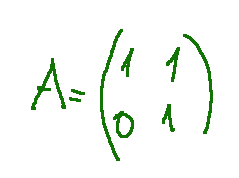 Consider the following system 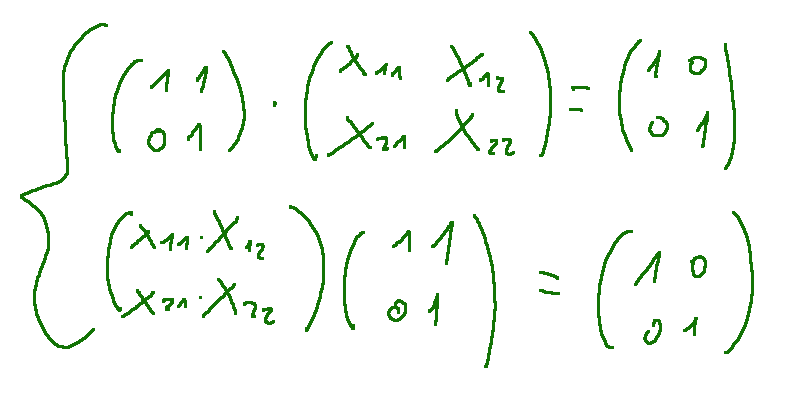 The unknown is a matrix. Now let's do the two products row by column. 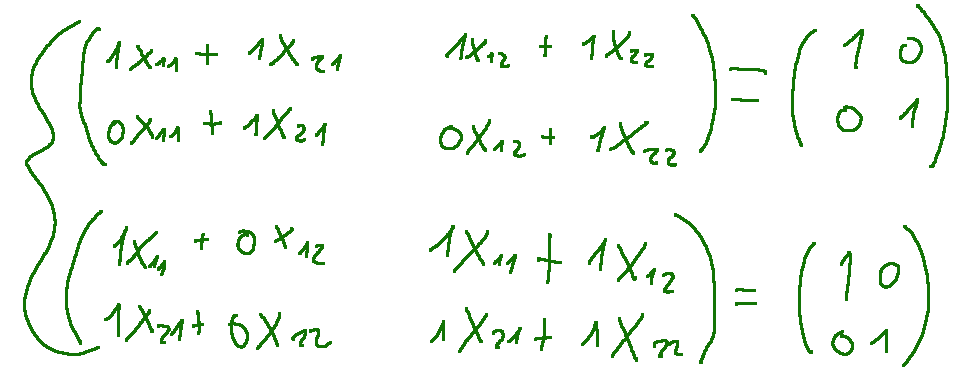 At this point we have a system of 8 equations 1 x11 + 1 x21 = 1 1 x12 + 1 x22 = 0 0 x11 + 1 x21 = 0 0 x12 + 1 x22 = 1 1 x11 + 0 x12 = 1 1 x11 + 1 x12 = 0 1 x21 + 0 x22 = 0 1 x21 + 1 x22 = 1 For solution has the quaterna (x11,x12,x21,x22) = (1, -1, 0, 1) Let's do two checks with the first two rows and the last one 1 x11 + 1 x21 = 1 ---> 1 x 1 + 1 x 0 = 1 1 x12 + 1 x22 = 0 ---> 1 x -1 + 1 x 1 = 0 … 1 x21 + 1 x22 = 1 ---> 1 x 0 + 1 x 1 = 1 ***Conclusions*** Matrix multiplications are obtained by multiplying the rows with the columns. ***Question*** In my opinion matrix multiplications are not an easy thing to understand, what do you think? --- https://images.hive.blog/1536x0/https://files.peakd.com/file/peakd-hive/green77/gGQutTRs-hive-spacer.png --- **[ITALIAN]** **04-11-2024 - Geometria analitica - Esempio moltiplicazione di matrici [EN]-[IT]** Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto (code notes: X_086) ***Esempio moltiplicazione di matrici*** Procediamo con la moltiplicazione tra le seguenti matrici 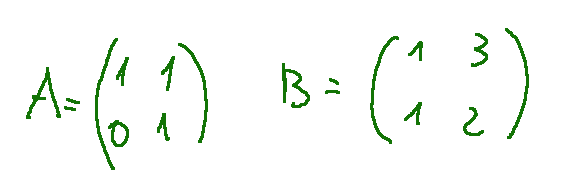 Il risultato per noi sarà la matrice C che avrà i seguenti termini come risultato c11=a11⋅b11+a12⋅b21 c12=a11⋅b12+a12⋅b22 c21=a21⋅b11+a22⋅b21 c22=a21⋅b12+a22⋅b22 Andiamo a sostituire i termini c11=1⋅1+1⋅2 c12=1⋅3+1⋅2 c21=0⋅1+1⋅1 c22=0⋅3+1⋅2 Otterremo i seguenti risultati c11=1⋅1+1⋅2 = 1 + 2 = 3 c12=1⋅3+1⋅2 = 3 + 2 = 5 c21=0⋅1+1⋅1 = 0 + 1 = 1 c22=0⋅3+1⋅2 = 0 + 2 = 2 Quindi la matrice risultante sarà la seguente 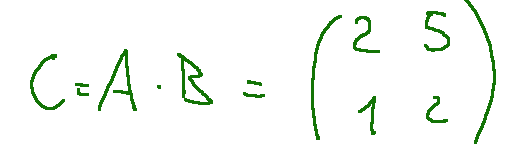 **Matrice inversa** Proviamo a trovare la matrice inversa di 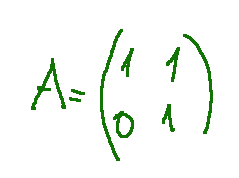 Consideriamo il seguente sistema 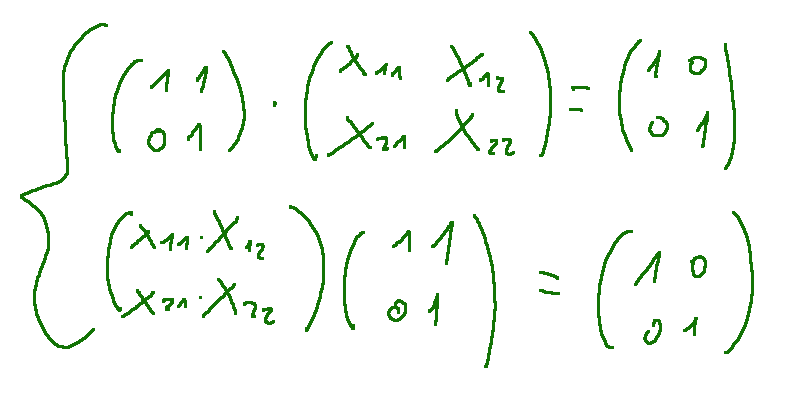 L’incognita è una matrice. Ora facciamo i due prodotti righe per colonne. 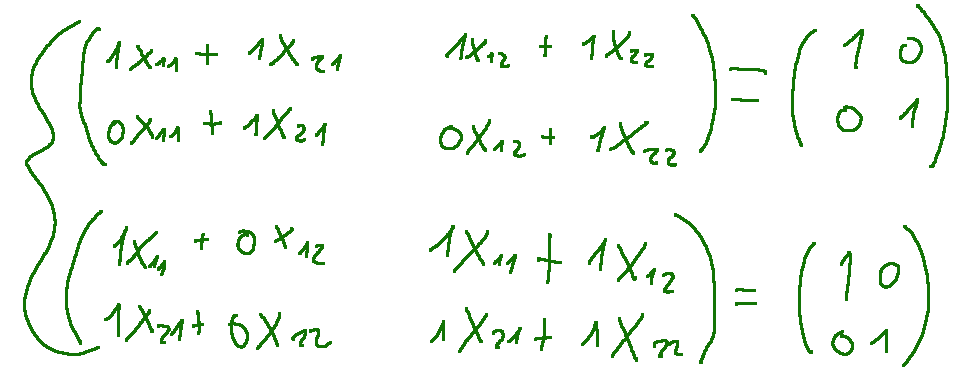 A questo punto abbiamo un sistema di 8 equazioni 1 x11 + 1 x21 = 1 1 x12 + 1 x22 = 0 0 x11 + 1 x21 = 0 0 x12 + 1 x22 = 1 1 x11 + 0 x12 = 1 1 x11 + 1 x12 = 0 1 x21 + 0 x22 = 0 1 x21 + 1 x22 = 1 Per soluzione ha la quaterna (x11,x12,x21,x22) = (1, -1, 0, 1) Facciamo due verifiche con le prime due righe e l’ultima 1 x11 + 1 x21 = 1 ---> 1 x 1 + 1 x 0 = 1 1 x12 + 1 x22 = 0 ---> 1 x -1 + 1 x 1 = 0 … 1 x21 + 1 x22 = 1 ---> 1 x 0 + 1 x 1 = 1 ***Conclusioni*** Le moltiplicazioni con le matrici si ottengono moltiplicando le righe con le colonne. ***Domanda*** Secondo me le moltiplicazioni tra matrici non sono una cosa facile da comprendere, voi che ne pensate? **THE END**
👍 dinamida, makeitreal95, dexpartacus, pab.ink, healthymary, hardrockcrypto, marianaemilia, shaidon, dosh, goliathus, hive-world, seuamiguto, emd012, jpleron, funnel, carl05, caaio, satoshil, xrayman, adulruna, lobaobh, highfist, prosocialise, genepoolcardlord, tobias-g, pedrocanella, anjanida, brucolac, brando28, hkinuvaime, qyses, kojiri, elfino28, stefanialexis, gabrielrr17, pardinus, gomster, bastter, carlosro, canellov, dudeontheweb, deggial, garlet, giemo, ilcontabile, libertypob27, nainaztengra, robibasa, cryptomonica, sportgamer, libertypal27, sweetunicorn, odb-contest, libertycrypto27, spurisna, blumela, nftfrappe, cur8, clifth, pixresteemer, sanjeev021, mesk, dragonmk47, khushboo108, pensieristupendi, skiptvads, libertyleo27, fedesox, grapthar, amestyj, abilitysend, stea90, p1k4ppa10, listnerds, uyoho, flquin, ctptips, thehockeyfan-at, lupega, he-index, newsposter, elianaicgomes, lexus083, alexbezimeni, svetlanaaa, marina007, sociopat, stanislav1, nellon, smolalit, fractal-team, peerfinance, aloysiusmbaba, lee1938, demonicore, giuatt07, feanorgu, marcusantoniu26, cryptoyzzy, tosolini, holovision.stem, stem.alfa, abh12345.stem, slider2990, joeyarnoldvn, dorkpower, juecoree.stem, saboin.stem, babytarazkp, sillybilly, meestemboom, hivebuzz, lizanomadsoul, manncpt, jnmarteau, crypticat, pinmapple, roelandp, princessmewmew, discovereurovelo, cranium, xsasj, musicandreview, gabrielatravels, steemitboard, arcange, afterglow, achimmertens, shainemata, laruche, aidefr, robotics101, dragibusss, egistar, wargof, imcore, lartist-zen, dspam, hive-129556, yggdrasil.laguna, stemgeeks, solominer.stem, lolz.ctp, moraviareosa, balaenoptera,