10-02-2025 - Analytical Geometry - System of Linear Equations [EN]-[IT]
hive-146620·@stefano.massari·
0.000 HBD10-02-2025 - Analytical Geometry - System of Linear Equations [EN]-[IT]
 --- *~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~* --- **ENGLISH** **10-02-2025 - Analytical Geometry - System of Linear Equations [EN]-[IT]** With this post I would like to give a brief instruction about the topic mentioned in the subject (code notes: X_75) ***System of Linear Equations *** One of the things that can be done through the study of matrices is to understand the existence of solutions of systems of linear equations. NOTE: Linear equations are equations in which the unknown (or unknowns) appear with exponent 1 and there are no terms with products between unknowns or more complex functions such as powers, roots or logarithms. Here is the general form, that is a linear equation in a single variable (x) 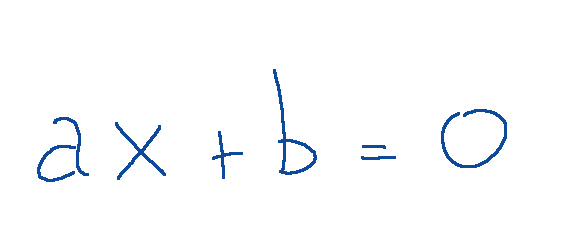 Where: -a and b are real numbers different from 0 -x is the unknown to be found **Example** Here we try to make an example trying to understand if the proposed system has a solution. *System of linear equations* 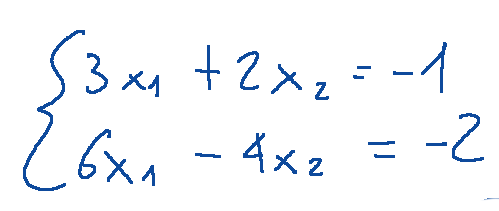 The incomplete matrix associated with the system is  It derives from the following extraction 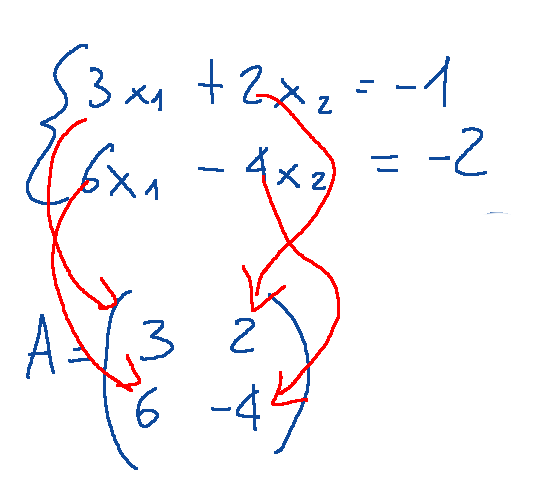 While the complete matrix associated with the system is 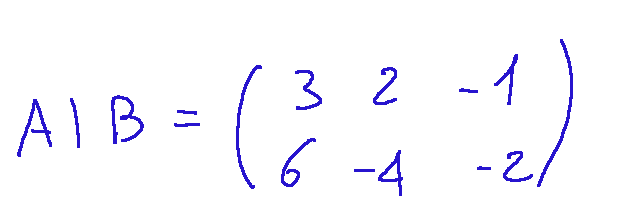 Which derives from the following extractions 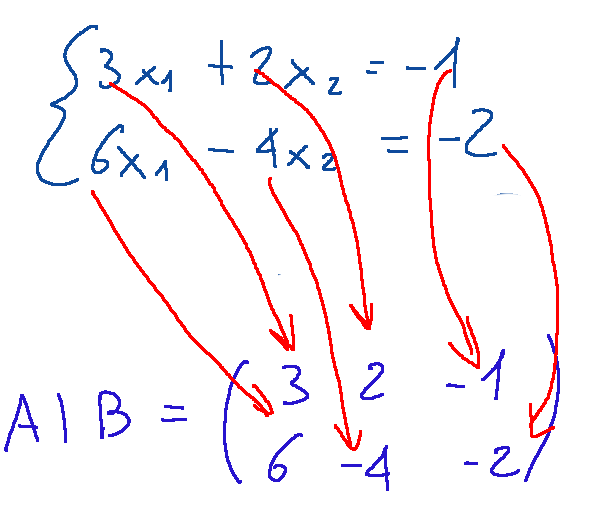 Now let's calculate the rank of the incomplete matrix A that we reproduce below:  The calculation of the determinant of the 2x2 matrix is following: 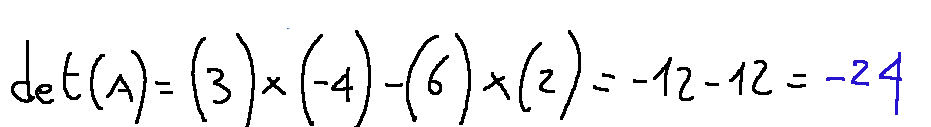 We can now come to the following conclusion. Since the determinant of the matrix A is different from zero,,, the rank of the incomplete matrix A is 2 Now let's move on to the calculation of the rank of the complete matrix 𝐴∣𝐵 The complete matrix 𝐴∣𝐵 was the following 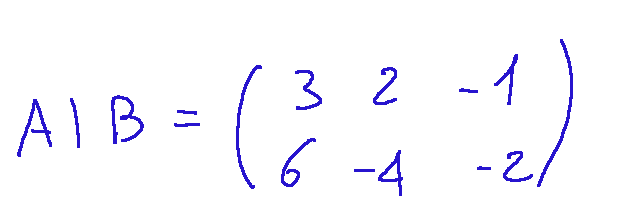 Let's reduce the complete matrix to the reduced form a scale: 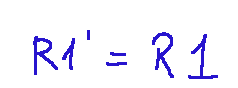 scale reduced form 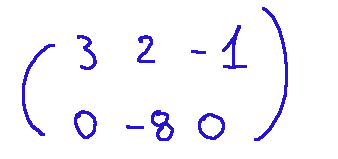 From here we deduce that there are two non-zero rows, the rank of the complete matrix 𝐴∣𝐵 is 2. Now if ri and rc indicate respectively the rank of the incomplete matrix and the rank of the complete matrix associated with the system we can state the following: 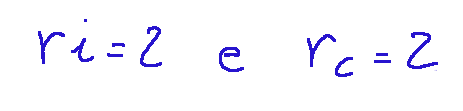 ri=2 and rc=2 *RESULT* Since ri = 2 and rc = 2, the system has a solution. ***Conclusions*** Through matrices we can study the existence of solutions of systems of linear equations ***Question*** Have you ever done similar exercises to discover the existence of solutions in systems of linear equations? --- https://images.hive.blog/1536x0/https://files.peakd.com/file/peakd-hive/green77/gGQutTRs-hive-spacer.png --- **[ITALIAN]** **10-02-2025 - Geometria analitica - Sistema di equazioni lineari [EN]-[IT]** Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto (code notes: X_75) ***Sistema di equazioni lineari *** Una delle cose che si possono fare attraverso lo studio delle matrici è capire l’esistenza delle soluzioni di sistemi di equazioni lineari. NOTA: Le equazioni lineari sono equazioni in cui l'incognita (o le incognite) compaiono con esponente 1 e non sono presenti termini con prodotti tra incognite o funzioni più complesse come potenze, radici o logaritmi. Qui di seguito la forma generale, cioè un'equazione lineare in una sola variabile (x) 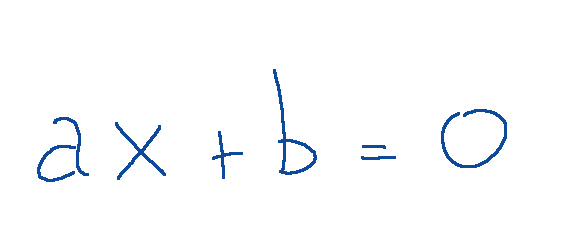 Dove: -a e b sono numeri reali diversi da 0 -x è l'incognita da trovare **Esempio** Qui di seguito proviamo a fare un esempio cercando di capire se il sistema proposto ha soluzione. *Sistema di equazioni lineari* 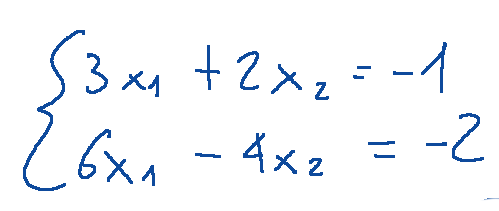 La matrice incompleta associata al sistema è  Deriva dalla seguente estrazione 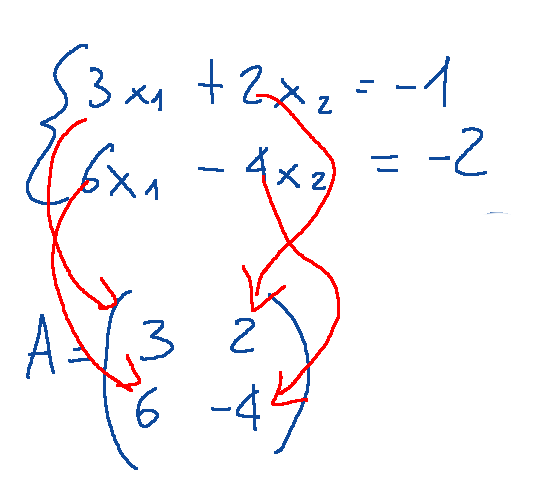 Mentre la matrice completa associata al sistema è 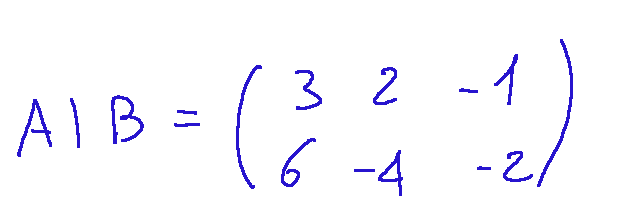 Che deriva dalle seguenti estrazioni 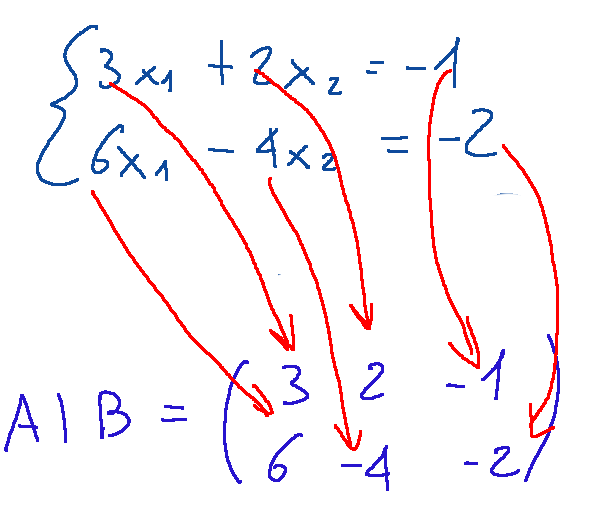 Ora calcoliamo il rango della matrice incompleta A che riproponiamo qui sotto:  Il calcolo del determinate della matrice 2x2 è la seguente: 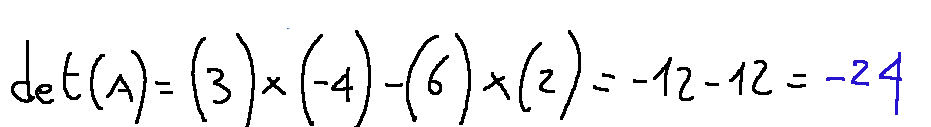 Possiamo ora arrivare alla seguente conclusione. Siccome il determinante della matrice A è diverso da zero,,, il rango della matrice incompleta A è 2 Ora passiamo al calcolo del rango della matrice completa 𝐴∣𝐵 La matrice completa 𝐴∣𝐵 era la seguente 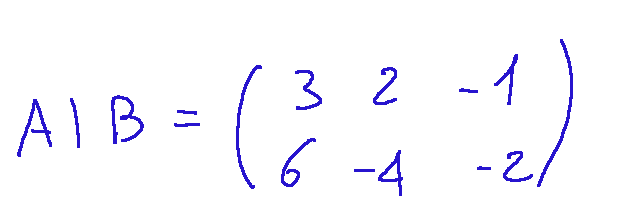 Riduciamo la matrice completa alla forma ridotta a scala: 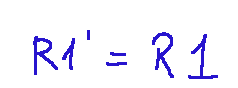 forma ridotta a scala 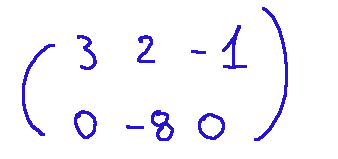 Da qui deduciamo che ci sono due righe non nulle, il rango della matrice completa 𝐴∣𝐵 è 2. Ora se ri ed rc indicano rispettivamente il rango della matrice incompleta e il rango della matrice completa associati al sistema possiamo affermare quanto segue: 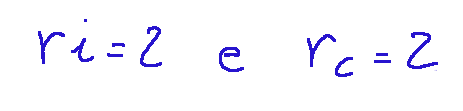 ri=2 e rc=2 *RISULTATO* Siccome ri = 2 ed rc = 2, il sistema ha soluzione. ***Conclusioni*** Attraverso le matrici si può studiare l’esistenza delle soluzioni di sistemi di equazioni lineari ***Domanda*** Avete mai fatto degli esercizi simili per scoprire l'esistenza di soluzioni in sistemi di equazioni lineari? **THE END**
👍 vimukthi, healthymary, dexpartacus, pab.ink, smartvote, hardrockcrypto, joeyarnoldvn, aurikan, pjansen.ctp, marianaemilia, funnel, stefanialexis, gabrielrr17, pardinus, dosh, gomster, caaio, anjanida, bastter, goliathus, hive-world, seuamiguto, carlosro, brucolac, brando28, vitoragnelli, adulruna, hkinuvaime, qyses, kojiri, lobaobh, jpleron, elfino28, highfist, genepoolcardlord, canellov, pedrocanella, emd012, deggial, menny.trx, garlet, voter, nainaztengra, axel-blaze, sweetunicorn, cryptomonica, sportgamer, libertypal27, ilcontabile, libertypob27, steveguereschi, libertycrypto27, spurisna, meppij, nftfrappe, cur8, odb-contest, clifth, pixresteemer, sanjeev021, mesk, dragonmk47, khushboo108, nongkamsailucky, pensieristupendi, skiptvads, libertyleo27, grapthar, stea90, lorenzopistolesi, marcusantoniu26, kkingg, bencwarmer, will91, abilitysend, hive-129556, fedesox, lozio71, demonicore, christybliss, peerfinance, kwick, steemitboard, marivic10, he-index, newsposter, elianaicgomes, lexus083, arcange, achimmertens, laruche, felt.buzz, aidefr, robotics101, jasonbu, twoitguys, hivebuzz, lizanomadsoul, manncpt, jnmarteau, crypticat, pinmapple, roelandp, discovereurovelo, fronttowardenemy, princessmewmew, cranium, xsasj, itchyfeetdonica, tikki00taffi, kimzwarch, gabrielatravels, egistar, iptrucs, vindiesel1980, p1k4ppa10, balaenoptera, discovery-it, waivio.curator, spiceboyz, gianluccio, ciuoto, carolineschell, marcolino76, alequandro, piumadoro, sbarandelli, a0i, vittoriozuccala, spaghettiscience, phage93, cooltivar, idayrus, nattybongo, coccodema, jessica.steem, middleearth, adinapoli, mfarinato, juanbg, lallo, titti, stregamorgana, yanezdegomera, meeplecomposer, tinyhousecryptos, maruskina, victoriaxl, omodei, medussart, capitanonema, damaskinus, marcellasunset, discovery-blog, ghastlygames, peterpanpan, matteus57, joseq1570, bindalove, repayme4568, maridmc, farmingtales, franvenezuela, jrjaime, arc7icwolf, cryptogillone, digy, joyyusuf, yzamazing, blip-blop, iamscinttwister, ghilvar, sararossi, juwon-btc, armandosodano, dannewton, eolianpariah2, sunisa, earthsea, jlsplatts, denisda, doodle.danga, vancouverdining, kharrazi, simgirl, andre.btc, carrinm, anutta, joseluis91, holovision.stem, moraviareosa,