@kenchung 设计的<a href="https://steemit.com/contest/@kenchung/question-mathematics-programming-competition-7">[Question] Mathematics × Programming Competition #7 [問題] 數學 × 程式編寫比賽 (第七回)</a>，对我来说，这个题已经非常难了。不过我还是尝试分别用数学方法和程序的方法来解答这个题：

<h1>（一）数学方法</h1>

我来说说我整个思路哈。

<h3>1. 分析角的变化</h3>

在正方形中，任意取一点。与正方形下边的两个点相连接。

显然，这个点越往下，夹角越大；这个点越往上，夹角越小。如下图：

![1.jpg](https://steemitimages.com/DQmSu4wFpUPDSVydCdWtj45Z2yFHvgTxUasD3UkJTExy1aq/1.jpg)

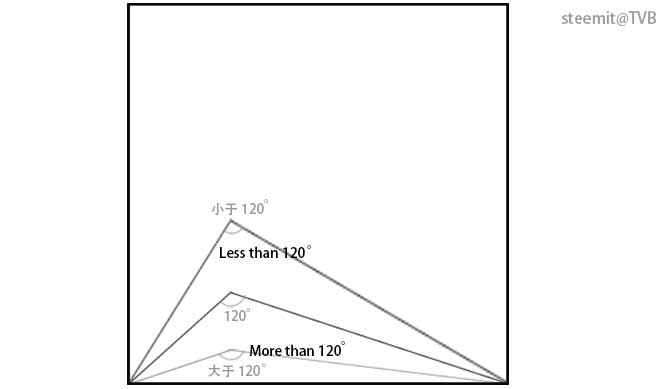
其中，有一个角是120度。而这个点在左右移动时，在不同的高度上，可以形成不同的120度角。把这些120度角的顶点连接起来，形成的轨迹，如下图：

![2.jpg](https://steemitimages.com/DQmViB6KfZyUw4CzcN6wW5z8ymWkEn5AUn6NZwHnWm3M1uk/2.jpg)

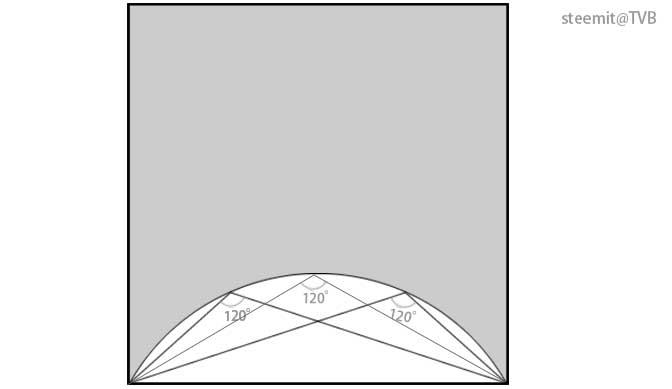
<h3>2. 找到临界线</h3>

如上图，这是一个弧形，圆形的一部分。只有圆，弧上的圆周角都是120度。初中数学，等弦对等角。

而这个弧线，就是临界线。正方形内部，弧线上方的点，与正方形下边连接形成的顶角，显然都小于120度。

><h2>On the arc, the angle in a circular segment is 120°.
<br>Above the arc, the angle is lese than 120°, and below the arc, the angle is more than 120°.</h2>

<h3>3. 确定范围</h3>

那么，相应的，对应正方形的四条边，分别可以绘制四条弧线，而这这四条弧线夹的部分：

左弧线的右侧、右弧线左侧、上弧下的下方、下弧线的上方，同时满足这四个条件，在正方形内部的部分，也是同时与正方形各点，所夹顶角小于120°的部分啦，如下图：

![3.jpg](https://steemitimages.com/DQmYskniPkrDayTamw7eYsMip18JRf4XdSfy9BWJoXTYL3q/3.jpg)

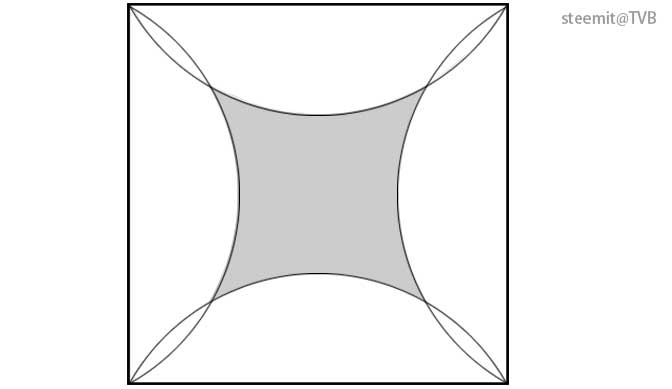
<h3>4.计算阴影面积</h3>

<h5>(1)计算圆的半径</h5>

把圆画出，正方形的边长是弦，弦所对的圆周角是120度，所以弦所对的大、小圆心角分别为240度和120度。

把正方形的边长设为1。圆的半径计算如下图：

![4.jpg](https://steemitimages.com/DQmbdp5MZUz8MX8MvmrFBnFUgrBqDpCRMR9cGtZYPorTBEd/4.jpg)

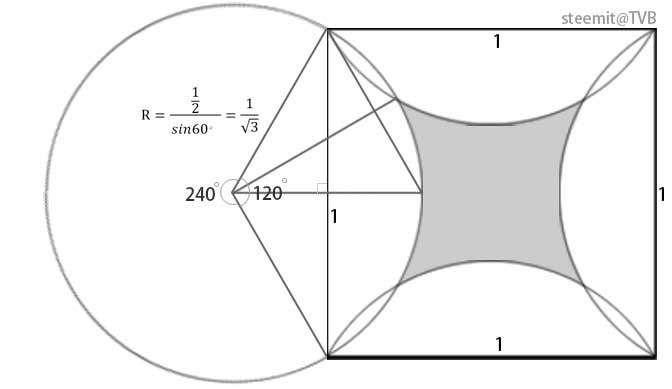
接下就是计算面积啦。

<h5>(2)计算粉色弓形面积</h5>

![5.jpg](https://steemitimages.com/DQmVmXsKQwk96sHFtJxh4VQFbGKVNLBMdPY3d5TxchZPzFt/5.jpg)
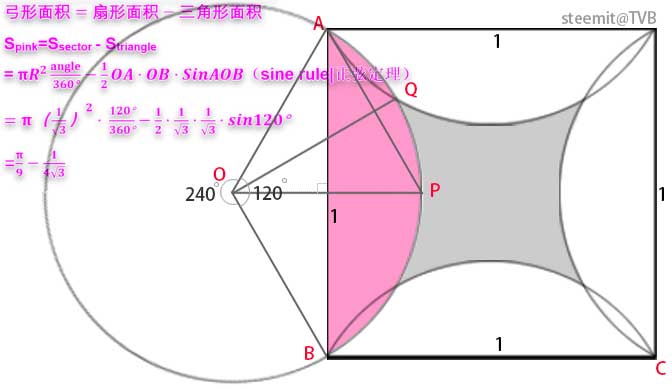
这里，三角形面积计算使用了一下正弦定理哈，发公式太费事了，大家自行百度或谷歌吧。

<h5>(3)计算蓝色弓形面积</h5>

如图：
![6.jpg](https://steemitimages.com/DQmVX7qaixHrg3G6hkyj6wXCot67HQ9cviUWtHcuCgi9QnZ/6.jpg)

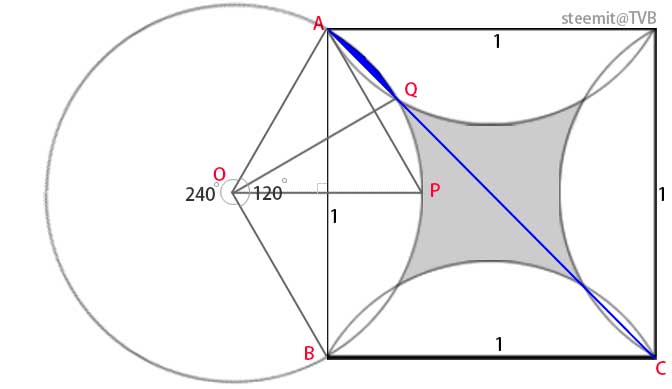
在等腰三角形AOB中，∠AOB=120°。所以∠BAO=30°。

由于AC是正方形对角线，所以角∠AB=45°。所以∠QAO=∠QAB+∠BAO=45°+30°=75°

三角形AOQ是等腰三角形，所以角∠QO也等于75°。

扇形AOQ的顶角AOQ是180-75-75=30°。

><h2>①
ΔAOB is a isoceles triangle 
∠AOB=120°
=> ∠BAO=30°
<br>②
AC is the diagonal
=> ∠AB=45°
<br>③
①②=>∠QAO=∠QAB+∠BAO=45°+30°=75°
<br>④
③,  ③,  ΔAOQ is a isoceles triangle
=>∠AOQ=180°-2×75°=30°</h3>

所以蓝色小弓形的面积计算如下图：

![7.jpg](https://steemitimages.com/DQmVx9iAAVxmiqddayepFQYQYBqiNbktYW8Ajv2ax6JaChC/7.jpg)

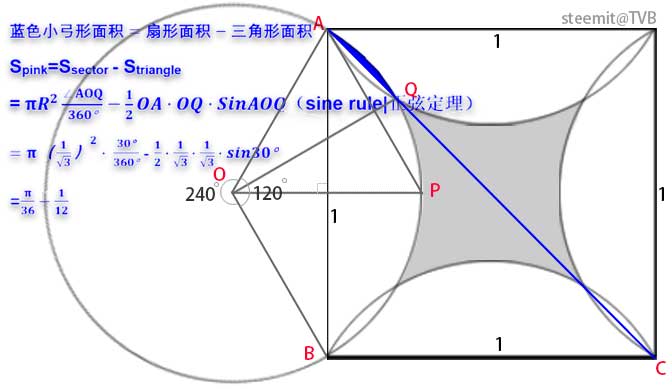
<h5>(4)计算阴影面积</h5>

阴影面积=正方形面积-4X粉色弓形面积+8X蓝色弓形面积=0.21255

因为，减粉色时，相交的小叶片被重复减了四块，即8块蓝色弓形

<h5>(4)计算概率</h5>

概率=阴形面积/正方形面积=0.213/1=0.21255

四舍五入0.213或者21.255%


<h1>（二）编程方法</h1>
我就是利用PHP的反正切函数atan()

同样还是把正方形边上看作1，把点距离正方形一个点的距离设为 $i $j，为了提高精度，每0.0001增加一点。

因为从每个端点出发的情况都是相同的，所以我作循环的时候就增加到0.5，这样能减少四分之三的运算量。

为了减少运算量，我用四层if嵌套。

	<?php
	$up=2*pi()/3;
	$m=0;
	$n=0;
	for($i=0.0001; $i<0.5; $i+=0.0001)
	{
		for($j=0.0001; $j<0.5; $j+=0.0001)
		{
			$m++;
			if(atan($i/$j)+atan((1-$i)/$j)<=$up)
			{
				if(atan($j/$i)+atan((1-$j)/$i)<=$up)
				{
					if(atan($i/(1-$j))+atan((1-$i)/(1-$j))<=$up)
					{
						if(atan($j/(1-$i))+atan((1-$j)/(1-$i))<=$up)
						{
							$n++;
						}
					}
				}
			}
		}
	}
	echo $n/$m;
	?>

<h3>我这个是暴力的方法，我感觉并不好，期待其他朋友更简便的编程算法。</h3>

<h3>算了我调大点精度吧，不然太暴力了，我在本地环境下运行都特别慢。</h3>
把精度从0.0001调到0.0005：

	<?php
	$up=2*pi()/3;
	$m=0;
	$n=0;
	for($i=0.0005; $i<0.5; $i+=0.0005)
	{
		for($j=0.0005; $j<0.5; $j+=0.0005)
		{
			$m++;
			if(atan($i/$j)+atan((1-$i)/$j)<=$up)
			{
				if(atan($j/$i)+atan((1-$j)/$i)<=$up)
				{
					if(atan($i/(1-$j))+atan((1-$i)/(1-$j))<=$up)
					{
						if(atan($j/(1-$i))+atan((1-$j)/(1-$i))<=$up)
						{
							$n++;
						}
					}
				}
			}
		}
	}
	echo $n/$m;
	?>