<center>![1416339913831.png](https://steemitimages.com/DQmXaMJSP1Acq3czRZawaNegS1AddfhbZoAAXeDioEWFyf2/1416339913831.png)</center>
<h1>What is a factorial</h1>
<p>A factorial is represented by the following pattern:</p>
<h3>1!=1</h3>
<h3>2!=2*1</h3>
<h3>3!=3*2*1</h3>
<br>
<p>More generally the algorithm is as follows:</p>
<h3>n!=(n-1)(n-2)(n-3)... for n=1,2,3....</h3>
<br>
<p>Notice that I purposely skipped 0! because it might not make sense yet since 0!=1. Moreover all fractions and all negative numbers were not included in the definition of n! This definition is very limiting so there is a need for a better definition of a factorial for such applications. </p>

<h1> A more versatile definition of a factorial</h1>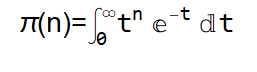
![Capture004.PNG](https://steemitimages.com/DQmct6q2wueJMHbYjTJAGV1YozVi7caKPWpmz2vbmeqxiGB/Capture004.PNG)
<br>
<p> This definition extends what you can do significantly and now the 0! can be shown as follows:</p>
https://steemitimages.com/DQmZ6jkSPBqYt9fJboZvfrbv1PCBrDPSbE69vTBriEyPgbf/Capture005.PNG
<p> There is a lot more you can do with this formula for exmaple now, it is possible to move away from integers and begin to use fractions of the factorial.</p>
<h3> 1/2! is solved as follows:</h3>
https://steemitimages.com/DQmUSYG3D4ZTFgz1ZpWAU9PDdGZcastawpsXsrGwXT17X8r/Capture007.PNG
<p> The n can essentially be anything just for show lets plug into mathematica 1!, 2!, and 3!</p>
<h3>1!</h3>
https://steemitimages.com/DQmSgtWcAaZcqk2svhArdQBetG8Y1BXhXoAjVs7dBeNs3pp/image.png
<h3>2!</h3>
https://steemitimages.com/DQmW5KChtLXGLXrU8gfgoqhFmCQ3pSnbmFNaaPv8PsZ68Jm/Capture009.PNG
<h3>3!</h3>
https://steemitimages.com/DQmbXDe5HPj3b8LQ1B33F1Qd4xa54cAjadaWk8ctyw5xiKV/Capture010.PNG
<p> Honestly I really did not want to do this by hand because it was too much work hopefully you all prove this to yourselves by hand if you don't believe me.</p>