OPTIMIZACIÓN MATEMÁTICA, EL MODELO DE TRANSPORTE COMO CASO ESPECIAL DEL MODELO DE PROGRAMACIÓN LINEAL
steemstem·@ydavgonzalez·
0.000 HBDOPTIMIZACIÓN MATEMÁTICA, EL MODELO DE TRANSPORTE COMO CASO ESPECIAL DEL MODELO DE PROGRAMACIÓN LINEAL
<div class="text-justify"> </div><div class="text-justify"><br></div><div class="text-justify"> <b>Fuente: @ydavgonzalez </b> Saludos a toda la comunidad de #STEEMSTEM, #STEM-ESPANOL y de Steemit en general, el día de hoy les comparto un post relacionado con la optimización matemática específicamente un tema perteneciente a la Investigación de Operaciones conocido como el modelo de transporte. En la programación lineal existe un tipo de problema relacionado con el transporte de artículos desde varias fuentes (por lo general fábricas) hasta diversos destinos (por lo general almacenes) satisfaciendo ciertas restricciones relacionadas con la oferta y la demanda, el transporte debe ser realizado con el objetivo de minimizar los costos, de esta forma, se trata también de un modelo de programación lineal que cuenta con una estructura especial conocido como el modelo de transporte, debido a que dicho problema se basa en un modelo de programación lineal puede ser resuelto mediante la aplicación del método simplex, sin embargo, su estructura especial permite aplicar un algoritmo específico que simplifica el proceso de solución. # DEFINICIÓN DEL MODELO Básicamente se trata de un problema en el que existen m fuentes y n destinos, por cada ruta, es decir, transporte de la fuente i al destino j, hay un costo asociado C<sub>ij</sub> según se muestra en la siguiente tabla: 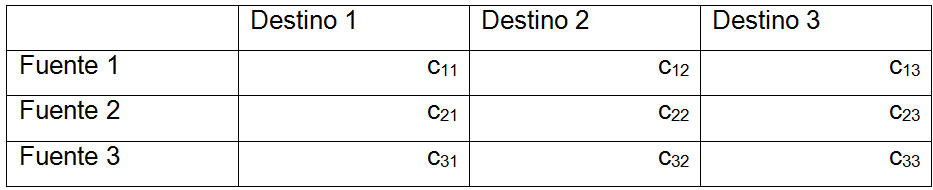 **Tabla N°1 Fuentes-Destinos modelo de transporte. Fuente: @ydavgonzalez.** Asumiendo que de la fuente i al destino j se transportan X<sub>ij</sub> unidades del producto y que cada fuente tiene una oferta determinada que se representa por O<sub>i</sub> y cada destino una demanda determinada del producto que se representa por D<sub>j</sub> la tabla del modelo de transporte se representaría de la siguiente forma: 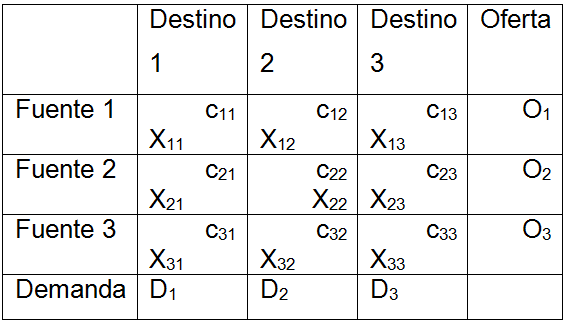 **Tabla N° 2 Fuentes-Destinos modelo de transporte. Fuente: @ydavgonzalez.** La tabla se ordena de esta manera debido a que la suma de todas las unidades enviadas desde la fuente i debe ser igual a la oferta disponible para dicha fuente, y la suma de todas las unidades enviadas al destino j debe ser igual a la demanda de dicho destino. En general el modelo de transporte se basa en la premisa de que el problema está balanceado, es decir, que la oferta total es equivalente a la demanda total, si el modelo no esta balanceado se puede restaurar el equilibrio al agregar una fuente o un destino ficticio según sea el caso. Ahora analizaremos un ejemplo en el cual se aplica el modelo de transporte, así como el procedimiento utilizado para resolverlo. ### Ejemplo N° 1 La **chocolatería el antojito caliente** tiene 3 sedes en la ciudad de Arequipa ubicadas en diferentes distritos (Paucarpata, Characato y Cerro Colorado), y debe transportar el chocolate a 4 destinos (San camilo, Plaza de Armas, Av Dolores y Yanahuara) los costos de transporte por unidad (en soles) así como la oferta y demanda se muestran en la siguiente tabla: 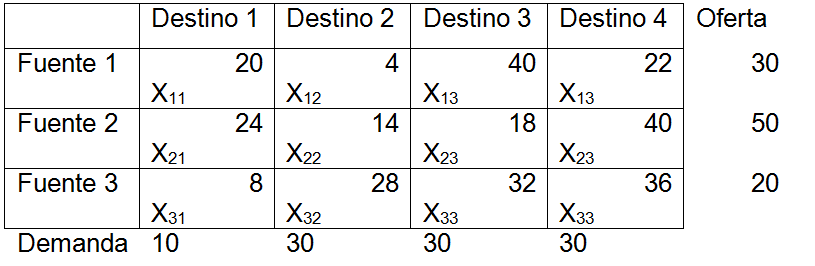 **Tabla N°3 Modelo inicial del ejemplo 1. Fuente: @ydavgonzalez.** Básicamente se trata de determinar la cantidad de chocolate que debe transportarse de cada destino a cada fuente (Variables X<sub>ij</sub>) de modo que se satisfagan las restricciones de oferta y demanda y se minimice el costo del transporte. Para resolver el problema se debe determinar una solución básica de inicio a partir de la cual mediante la determinación de las variables de entrada y salida de la tabla se va iterando hasta llegar a la solución óptima. ## DETERMINACIÓN DE LA SOLUCIÓN BÁSICA DE INICIO – MÉTODO DE LA ESQUINA NOROESTE El método de la esquina noroeste o de la esquina superior izquierda, comienza en la esquina superior izquierda a la cual asigna el mayor valor posible sin exceder las restricciones de oferta y demanda. 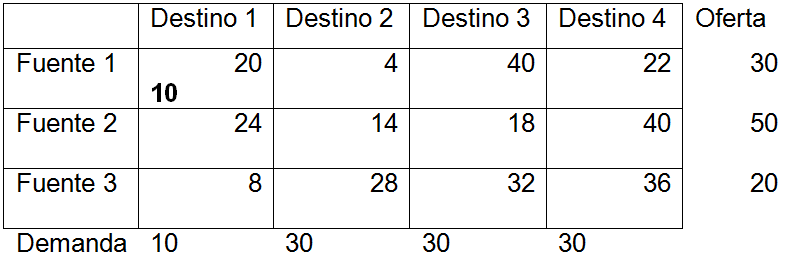 **Tabla N°4 Método de la esquina noroeste. Fuente: @ydavgonzalez.** No se puede asignar un valor mayor a 10 debido a que la demanda para el destino 1 es de 10 unidades, como ya la demanda para el destino 1 (columna 1) está satisfecha salimos de esa columna hacia la siguiente columna. 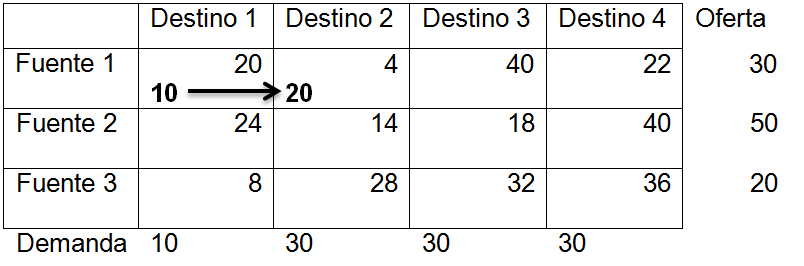 **Tabla N° 5 Cálculos del Método de la esquina noroeste. Fuente: @ydavgonzalez.** Asignamos 20 a la variable X<sub>12</sub> debido a que con ese valor la oferta alcanza el máximo valor posible y luego pasamos a la fila inferior debido a que la oferta de la fila 1 ya esta completa, en caso de que la oferta y demanda alcancen el máximo al mismo tiempo se elige si se debe dar por completada la oferta o demanda y se pasa a la siguiente fila o columna (según sea el caso) colocando cero como valor para no exceder las restricciones. Aplicando el mismo procedimiento se encuentra la solución básica inicial 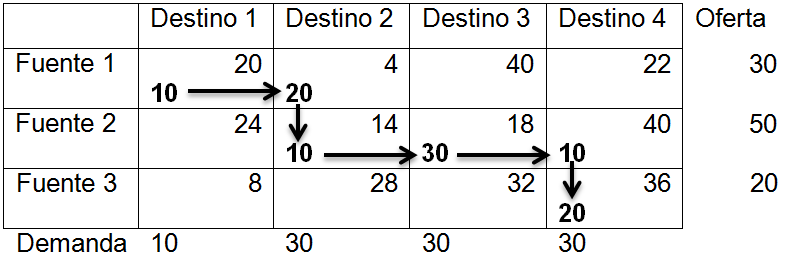 **Tabla N°6 Solución básica inicial Método de la esquina noroeste. Fuente: @ydavgonzalez.** Se observa que el costo del transporte en esta solución básica de inicio viene dado por la suma del producto del número de unidades transportadas de la fuente i al destino j multiplicados por los costos C<sub>ij</sub>, las variables que no tengan valores en la tabla se asumen como cero al calcular el costo del transporte. 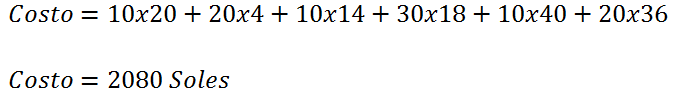 ## CÁLCULOS ITERATIVOS – MÉTODO DE LOS MULTIPLICADORES Una vez encontrada la solución básica de inicio, se procede a aplicar el método de los multiplicadores, asociando los multiplicadores u<sub>i</sub> y v<sub>j</sub> a las filas i y las columnas j de la tabla del modelo de transporte 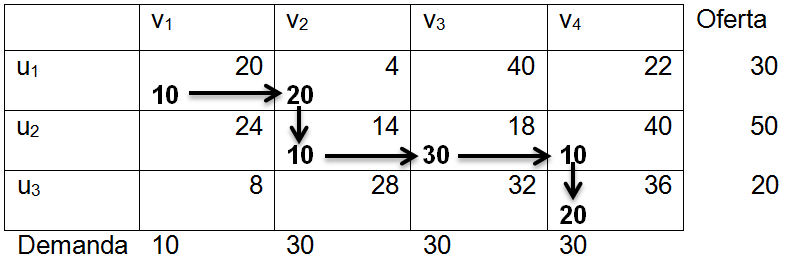 **Tabla N°7 Solución básica inicial Método de la esquina noroeste. Fuente: @ydavgonzalez.** Ahora para cada variable básica, es decir, que este en la solución básica inicial obtenida por el método de la esquina noroeste, se procede a asociar los multiplicadores según la siguiente ecuación 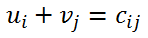 Según la solución básica del ejemplo se obtiene 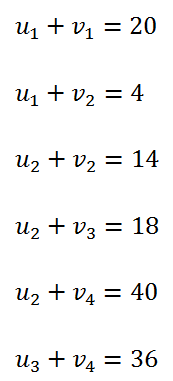 Para resolver se iguala alguno de los u<sub>i</sub> a cero y se resuelve para los demás valores 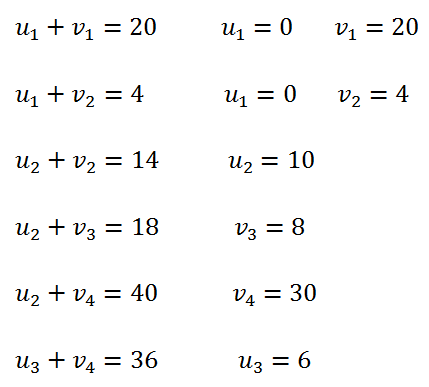 A continuación se usan los u<sub>i</sub> y v<sub>j</sub> obtenidos para evaluar las variables que no estén en la base con la siguiente expresión 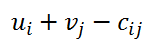 Obteniendo  **Tabla N°8 Valores de las variables no básicas por el método de los multiplicadores. Fuente: @ydavgonzalez.** Estos valores se representan en la tabla de transporte asignándolos a las variables que no estén en la solución básica inicial, quedando la nueva tabla de la siguiente forma 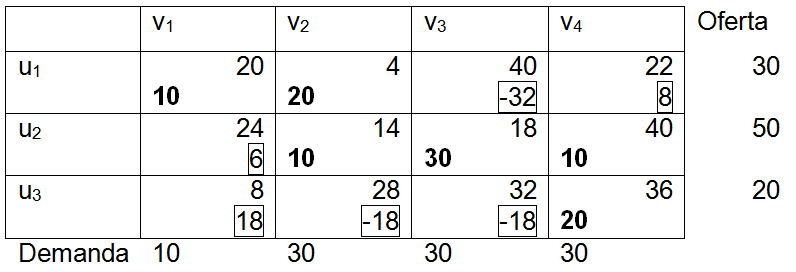 **Tabla N°9 Iteración N° 1 Modelo de Transporte. Fuente: @ydavgonzalez.** Luego para obtener la variable de entrada, se toma la variable no básica cuyo valor sea mayor 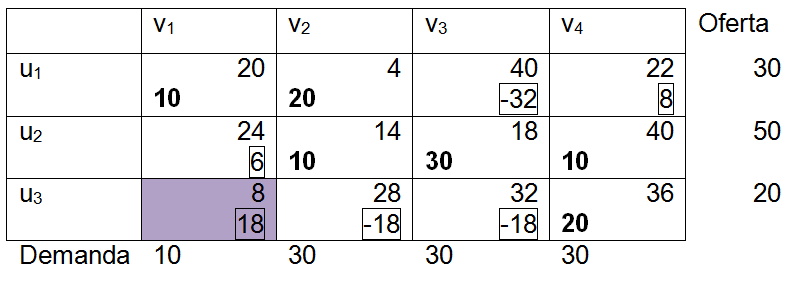 **Tabla N°10 Variable de entrada Iteración N° 1. Fuente: @ydavgonzalez.** Es decir X<sub>31</sub> es la variable de entrada, lo cual implica que se debe transportar desde la fuente 3 al destino 1 para minimizar los costos, es decir, en la siguiente iteración la variable X<sub>31</sub> tendrá un valor asignado ∆. A incrementar el valor de X<sub>31</sub> por ∆ se debe mantener el equilibrio en la oferta y demanda, lo cual se logra mediante construir un ciclo cerrado entre la variable entrante y las variables básicas, omitiendo los valores que aparecen en recuadros pequeños, la nueva tabla sería 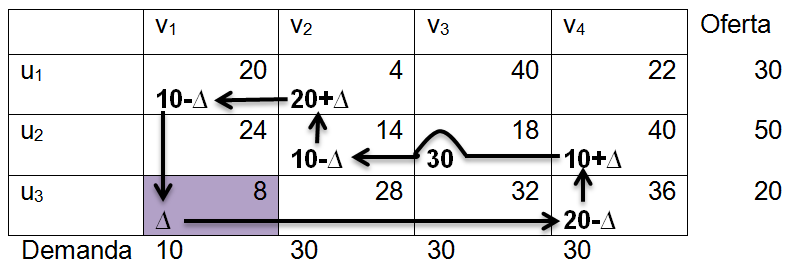 **Tabla N° 11 Construcción del ciclo Iteración N° 1. Fuente: @ydavgonzalez.** Podemos apreciar que al sumar los nuevos valores tanto de las filas como de las columnas se conserva el equilibrio, se observa también que para cada fila o columna el ciclo empieza en un extremo y termina en el otro extremo que sea parte de la solución básica inicial. Ahora asignamos a ∆ el mayor valor posible de manera que ninguna de las variables básicas de la tabla anterior sea negativa, teniendo en cuenta las relaciones mostradas el mayor valor posible es ∆=10, y resolvemos para dicho valor, la variable básica que nos de cero será la variable de salida en caso de que dos variables básicas nos den cero elegimos cualquiera como variable de salida, este caso sucede en el problema que estamos resolviendo en el cual elegiremos a X<sub>11</sub> como variable de salida. Por ser X<sub>11</sub> la variable de salida ya no colocamos su valor en la nueva tabla en cambio a pesar de que X<sub>22</sub> nos dio cero como no es nuestra variable de salida mantenemos el valor de cero. 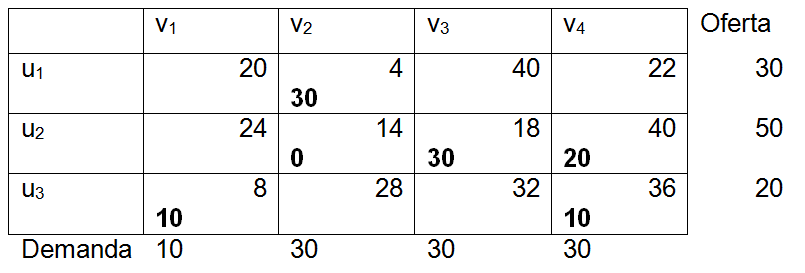 **Tabla N°12 Solución Básica Iteración N° 1. Fuente: @ydavgonzalez.** ### Iteración N° 2 Se repite el calculo de los multiplicadores u<sub>i</sub> y v<sub>j</sub> teniendo en cuenta la nueva solución básica 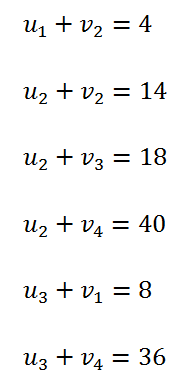 Asignando a 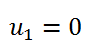 Obtenemos 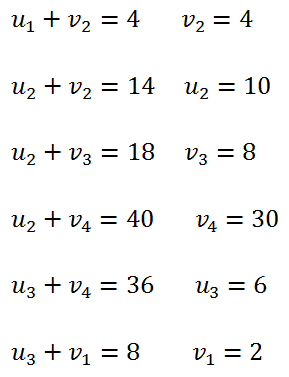 Para las variables no básicas se evalúa 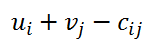 Obteniendo  **Tabla N°13 Valores de las variables no básicas por el método de los multiplicadores Iteración N° 2. Fuente: @ydavgonzalez.** Resultando en la siguiente tabla de transporte: 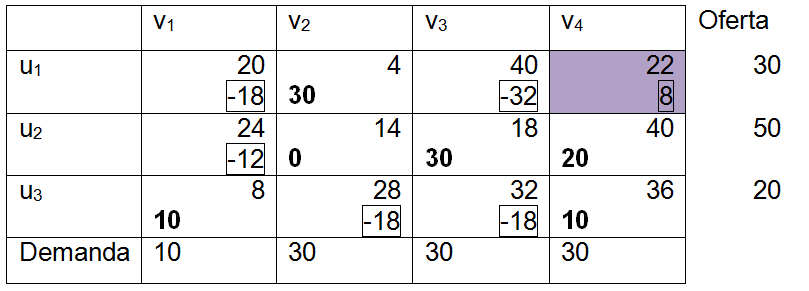 **Tabla N°14 Iteración N° 2 Modelo de Transporte. Fuente: @ydavgonzalez.** La variable de entrada del modelo de transporte será la variable no básica que tenga el mayor valor, en este caso la variable de entrada es X<sub>14</sub> por tener el mayor valor, por lo tanto construimos el ciclo al igual que en la iteración anterior. 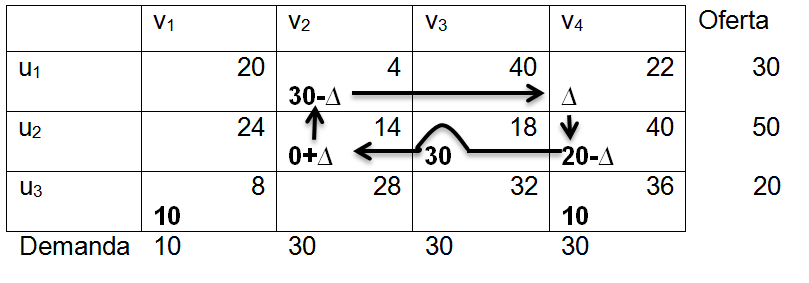 **Tabla N°15 Iteración N° 2 Construcción del ciclo. Fuente: @ydavgonzalez.** El mayor valor que puede asumir ∆ es 20, para dicho valor se obtiene 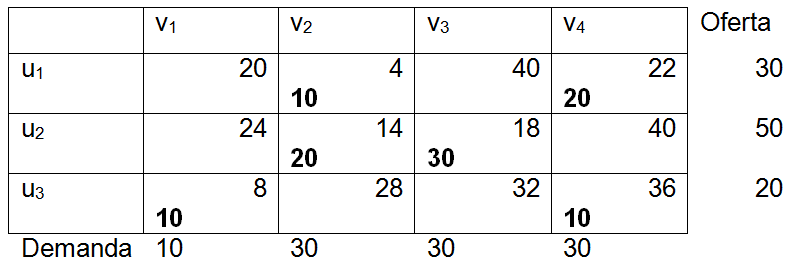 **Tabla N°16 Iteración N° 2 Solución básica. Fuente: @ydavgonzalez.** ### Iteración N° 3 Se repite el calculo de los u<sub>i</sub> y v<sub>j</sub> teniendo en cuenta la nueva solución básica 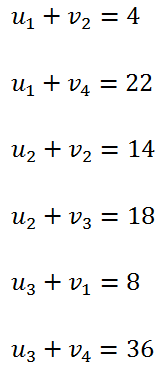 Asignando a 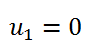 Obtenemos 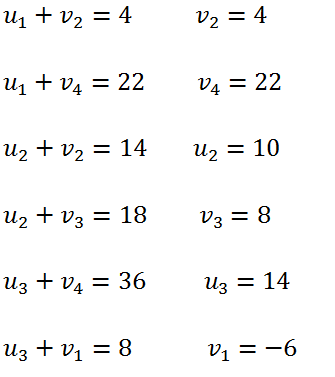 Para las variables no básicas se evalúa 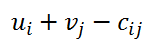 Obteniendo  **Tabla N°17 Iteración N° 3 Valores de las variables no básicas por el método de los multiplicadores. Fuente: @ydavgonzalez.** Obteniendo la siguiente tabla de transporte 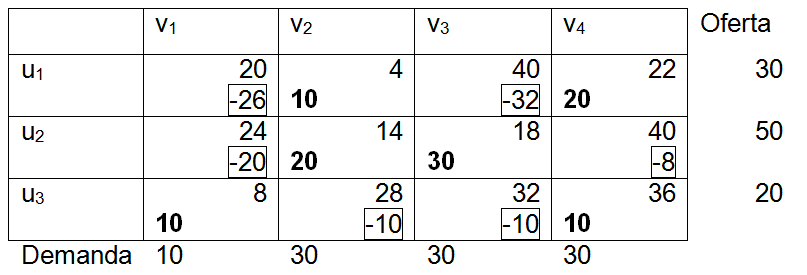 **Tabla N°18 Iteración N° 3 Modelo de Transporte. Fuente: @ydavgonzalez.** Como todos los 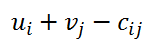 Son negativos en esta tabla la solución es óptima, por lo tanto la chocolatería debe transportar de la fuente 1: 10 unidades al destino 2 y 20 unidades al destino 4, de la fuente 2: 20 unidades al destino 2 y 30 unidades al destino 3 y de la fuente 3: 10 unidades al destino 1 y 10 unidades al destino 4, de esta forma satisface la oferta y demanda al costo mínimo. 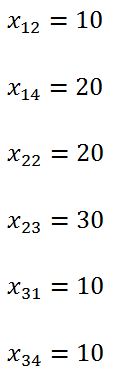 Con un costo asociado de 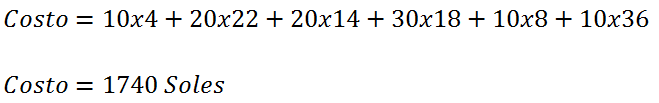 # CONCLUSIONES 1. La optimización matemática posee una gran cantidad de aplicaciones en problemas de la vida cotidiana y en economía. 2. El modelo de transporte debido a poseer una estructura de programación lineal puede ser resuelto mediante el método simplex, sin embargo, el algoritmo de transporte es un método más eficiente utilizado para resolver este modelo. 3. La relación entre el método simplex y el algoritmo de transporte tiene fundamentos matemáticos basados en la teoría de la dualidad. ## REFERENCIAS BIBLIOGRÁFICAS Y LECTURAS RECOMENDADAS 1. González (2018) <a href="https://steemit.com/stem-espanol/@ydavgonzalez/aplicacion-del-metodo-simplex-a-un-problema-de-maximizacion-de-ganancias-fundamentado-en-los-topicos-de-algebra-lineal">Aplicación del Método Simplex a un problema de maximización de ganancias fundamentado en los tópicos del Álgebra Lineal.</a> 2. González (2018) <a href="https://steemit.com/stem-espanol/@ydavgonzalez/optimizacion-matematica-en-modelos-de-programacion-lineal-aplicados-a-la-vida-cotidiana-metodo-simplex-de-las-dos-fases">Optimización Matemática en Modelos de Programación Lineal aplicados a la vida cotidiana, Método Simplex de las dos fases.</a> 3. González (2018) <a href="https://steemit.com/stem-espanol/@ydavgonzalez/resolucion-de-modelos-de-programacion-lineal-utilizando-la-herramienta-para-optimizacion-lingo-y-analisis-de-su-relacion-con-el">Resolución de Modelos de Programación Lineal utilizando la Herramienta para Optimización Lingo y Análisis de su relación con el Método Simplex.</a> 4. Taha (2004), Investigación de Operaciones. 7ma edición Editorial Pearson. _**Si deseas leer contenido científico de calidad en habla hispana te invito a revisar la etiqueta #STEM-ESPANOL donde podrás encontrar diversidad de temas, Matemática, Ingeniería, Física, Química, Biología, Medicina, Ciencia, Tecnología y mucho más.**_  **Logotipo del Área de Matemáticas de #STEM-ESPANOL** </div>
👍 elviento, veronicacoli, steemexpress, ordinaryamerican, optimizer, bluesniper, onidi, ettorat, nengaroto, erari, towimindu, uronge, edoro, runos, owedisisa, lopti, usaroof, motherboy, simplepim, estesel, gears5, iddeeci, ledsond, ingof, vuecrof, athererer, melisarou, saitoupli, reror, etambeese, rorerni, sutrisuti, inenend, exatoup, desong, icrorro, yuiglence, ecofaci, zidot, idict, vayuzhipsch, ervandkarapet, hunangalstyan, suggestboron, conditionkentish, ahullcortege, cwitosaw, soufflereports, saymonr, hellan, yomist, sartanond, titons, arero, rangondor, ezesting, laradyi, rillechi, roummid, amarenti, andowenda, minasyandianna, assaulenko, unarmedxyloid, shoemakerintegra, kabernee, killex, spudssleeping, pashafeloff, sera1995, nikvoronkov1984, anmal1990, haldunea, ratho, dont.stop, ichuad, andofon, sidsunt, teerouce, putsaleli, alala8, dealides, ulles, dashakarapetyan, gracefulestrogen, basiks, pferdynand, warblingunchin, stressedboiler, dearshy, friedradius, roma.kisov, andrey.levin92, ekarina10, nistin, neraptic, utousild, tintu, unend, actowh, ughaimomp, undate, engitora, edidrasa, arishis, ydavgonzalez, jga, ivymalifred, ennyta, criptoanarquista, luisal314, isisfemale, isgledysduarte, fabielblanchard, arequipa, leviackerman, joanni, sam-dmc, smvenezuela, lujuria, elowin, tavera509, onthewayout, lupafilotaxia, alaiza, lapp, steemtpistia, crassipes, agrovision, enmy, rutablockchain, arcange, vidayaventura, marialefleitas, helyorsini, danielvehe, dorada, pipitzi, blvg1910, interclone, alexos, angelik, jossduarte, marynessc, bellarulox, cj90, juanse24, steem-walking, gabrielperez0411, rafarod83, ikeror, readkr, blancowilson, nogriv, edibastard, finanzasid, enrique89, leonellaforever, ricardo993, ucdm, madefrance, isamarica, isaac007, elvigia, desdelaislanews, carlosmejias, vidente, yisusgtr, lisbth19, yenncanela, mauisa, aliriera, tresminotauros, armandeus2012, morillofrank17, alisalof, williams-68, chamerada, jascompositor, raphaelle, ubaldonet, lenonmc21, chriscuasicuerdo, viajeradelrio, aifer.escobar, rafasun, pattyrod85, marilem, deibysv, elvys, karii, caballodefuego, enmaoro, tecnol, monarcaazul, zullyscott, delpilar, djredimi2, reinaseq, steemstem, kevinwong, lemouth, adetola, rionpistorius, effofex, count-antonio, beautyinscience, dna-replication, alexander.alexis, fancybrothers, howo, alexzicky, tanyaschutte, felixrodriguez, mayowadavid, enzor, tristan-muller, fejiro, sco, rharphelle, shoganaii, jlmol7, real2josh, kingabesh, dedesuryani, de-stem, temitayo-pelumi, alexworld, ibk-gabriel, ascorphat, tombstone, arconite, bloom, kryzsec, helo, samminator, suesa, tsoldovieri, esteemguy, coolbuddy, mr-aaron, kenadis, gentleshaid, mathowl, terrylovejoy, olajidekehinde, dexterdev, alexdory, francostem, michaelwrites, deholt, purelyscience, stem.witness, abigail-dantes, delin.english, maticpecovnik, mondodidave73, geopolis, lesmouths-travel, doctor-cog-diss, testomilian, crazy-facts, miniteut, curie, corsica, mountain.phil28, kingswisdom, irishcoffee, gra, darkiche, stemng, jaycem, steemzeiger, biomimi, jrevilla, jent, zonguin, jasonbu, erikkun28, aalok, mattiarinaldoni, dragibusss, intellihandling, emmanuel293, scoora82, casiloko, moniroy, praditya, cameravisual, amin-ove, huilco, donasys, mtfmohammad, pflanzenlilly, faberleggenda, mohaaking, locikll, tuoficinavirtual, traviseric, galam, cryptokrieg, samest, gambit.coin, agbona, the.chiomz, teekingtv, joelagbo, djoi, menoski, thurllanie, emperorhassy, teemike, vact, diebaasman, aboutyourbiz, howtostartablog, phogyan, motivatorjoshua, speaklife, admiralsp, chimtivers96, sciencetech, anwenbaumeister, makrotheblack, hotsteam, markmorbidity, pinksteam, strings, loydjayme25, sissyjill, morbyjohn, bil.prag, hendrikdegrote, dashfit, lrsm13, leyla5, muliadi, reaverza, esaia.mystic, debbietiyan, trixie, beni96, phaazer1, chrisluke, nitego, operahoser, jpmkikoy, niouton, schroders, misterakpan, clweeks, derekvonzarovich, digitalpnut, sireh, beladro, qberryfarms, raymondspeaks, szokerobert, mrstaf, g0nr0gue, paddygsound, joendegz, sunnyali, kendallron, hansmast, moksamol, getrichordie, thatsweeneyguy, stahlberg, bavi, onethousandpics, creatrixity, didic, hardaeborla, ashfaaaq, cynicalcake, nolasco, neumannsalva, poodai, kimchi-king, drmake, tomatom, misia1979, avizor, call-me-howie, whoib, resteemer, akumar, irisworld, adamzi, ameliabartlett, technotroll, nigerian-yogagal, clement.poiret, kiikoh, gbemy, gangstayid, dbzfan4awhile, gabrielatravels, idkpdx, momimalhi, deividluchi, raghao, rhethypo, antigourmet, predict-crypto, ilovecryptopl, tuck-fheman, lola-carola, gmedley, click3rs, mininthecity, cjunros, justasperm, ejgarcia, zerokun, semtroneum, positiveninja2, slickhustler007, venalbe, adalhelm, stonecoin, andydream, zeldacroft, alom8, delegate.lafona, boynashruddin, alexanderrigov, hkmoon, reizak, zlatkamrs, lilianajimenez, jjohnson78, annaabi, pechichemena, as-abir, sarhugo, jan-mccomas, riche-gould, jlsplatts, abeyaimary, gordon92, jordan.white306, payger, shadown99, trang, angoujkalis, eu-id, dokter-purnama, jakesdewet, teukurival, brutledge, mladenpaunovic, talli-art, jcalero, elsll, outtheshellvlog, somegaming, naomipangolin, bflanagin, sina-adventure, velmafia, homefree, splatz, steem-with-ebay, darkstar1o9, goldkeys, lekang, allcapsonezero, eurodale, kothy, ambitiouslife, jingis07, gabyoraa, dtwo, berien, sivehead, kuku-splatts, luiyi-22, splatz-1, splatz-2, jk6276.mons, lenin-mccarthy, marshall117, jubei333, shayekh2, ykdesign, positiveninja, lil-splatts, reverseacid, cowpatty, juliamulcahy, tonyudo57, nicephoto, yaelg, dbddv01, fanta-steem, zest, bohemian.machine, jewlzie, communityisyou, kipswolfe, medicnet, peaceandwar, thescubageek, qwoyn, mahdiyari, lamouthe, vodonik, eniolw, wackou, drifter1, mammasitta, charlie777pt, stevenwood, longer, gpcx86, drifter2, diyanti86, desikaamukkahani, raoufwilly, alvin0617, imaloser, jiujitsu, danaedwards, shinedojo, gio6, youraverageguy, knightbjj, coinbrew, deadcountry, combatsports, wrestletalk, gracelbm, landria, opheliapoe, damzxyno, lacher-prise, drsensor, guchtere, rival, massivevibration, happychild, benleemusic, eric-boucher, robertbira, eroticabian, sanderdieryck, nicole-st, laurentiu.negrea, hhtb, yomismosoy, maaz23, lekosvapenglass, goodway, kafupraise, cryptosteemcoin, egotheist, langford, wargof, guga34, xanderslee, williams-owb, lk666, honeysara, cooknbake, hillaryaa, delph-in-holland, cordeta, christianyocte, mrxplicit, ivan-g, sunshinebear, apteacher, flatman, marehalm, senorcoconut, oghie, gosmire78, oclinton, danlipert, maribelf, marcela424424, utopian-io, sargoon, cryptouno, swapsteem, camilo12, josedelacruz, chwaqas, iradyjr, abneagro, anllelis, warofcraft,