<h4>¡Hola amigos de Hive Blog!</h4>

<h4>Reciban un cordial saludo.</h4>
 
<div class="text-justify">En el estudio de los movimientos oscilatorios uno de vital importancia es el que describe un péndulo.</div><p>
<div class="text-justify">El movimiento oscilatorio descrito por un péndulo es observado en la naturaleza y en una gran variedad de sistemas mecánicos simples y complejos. Entre sus principales aplicaciones encontramos la medición del tiempo y la obtención del valor de la gravedad.</div><p>
<div class="text-justify">Para pequeñas oscilaciones, el movimiento oscilatorio del péndulo es análogo al descrito por un sistema masa-resorte, por lo que obedece a las mismas leyes matemáticas que gobiernan un movimiento armónico simple.</div><p>
<div class="text-justify">Dada su importancia, en este trabajo analizaremos los fundamentos físicos y matemáticos del movimiento oscilatorio de un péndulo simple y determinaremos el valor de la gravedad a partir de las variaciones que experimenta el periodo de oscilación ante los cambios de longitud. </div>

<h3>Fundamentos teóricos </h3>

<div class="text-justify">Un péndulo simple está formado por un hilo inextensible de longitud “<b>L</b>” y masa despreciable, que sujeta una masa puntual “<b>m</b>” que se balancea respecto a un punto fijo.</div><p>
<div class="text-justify">Cuando la masa es desplazada un ángulo “<b>θmax</b>” respecto de su posición de equilibrio “<b>θ<sub>0</sub>=0</b>”, las fuerzas actuantes obligarán al cuerpo a moverse en una trayectoria circular o arco en el que la masa esta confinada debido al hilo que la sujeta con una fuerza de tensión “<b>T</b>”. </div><p>
<div class="text-justify">En la siguiente imagen se muestra un diagrama de cuerpo libre en el que están representadas la tensión ejercida por el hilo y la fuerza gravitacional “<b>mg</b>” con sus respectivas componentes. La fuerza tangencial “<b>mgsenθ</b>” es la fuerza restauradora que siempre va dirigida hacia la posición de equilibrio "<b>θ<sub>0</sub>=0</b>" y es opuesta al desplazamiento.</div>

<center>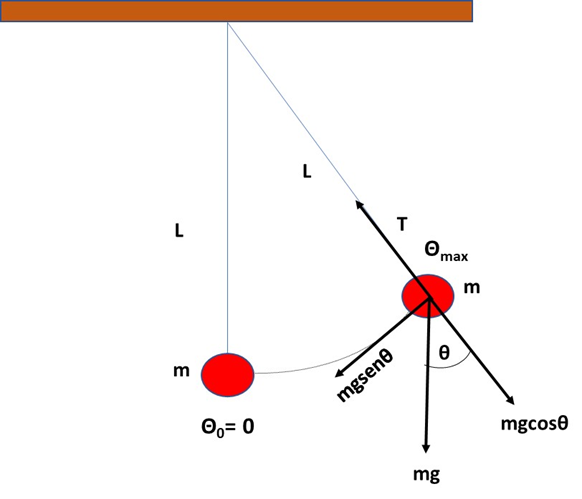![image.png](https://images.hive.blog/DQmUciGJKh2gw6RWksMtM9GVHd39bf7XRMyzxWha4kFAm4M/image.png)</center>
<center><em><sup>Figura 1. Diagrama de cuerpo libre en el péndulo simple 
(Elaborada por @lorenzor en Powerpoint)</sup></em></center>

<div class="text-justify">En la dirección tangencial tenemos de la segunda ley de Newton  (<b>∑F<sub>t</sub> =ma<sub>t</sub></b>) que:</div>
<center>https://images.hive.blog/DQmVZhtv4TBwS5cJFPTqEt5RY4sm8wr53KBuc2CbwgMgmga/image.png</center>

<div class="text-justify">Donde la aceleración tangencial  "<b>a<sub>t</sub></b>" está dada por el cambio de la magnitud de la velocidad "<b>v</b>",  según lo expresa la siguiente ecuación:</div>
<center>https://images.hive.blog/DQmcoSMZNfMusgPe6kuuP7KazoH64nvavb8Bq4EL4J7gj9V/image.png</center>
<div class="text-justify">Para determinar el valor de la velocidad de la masa en la trayectoria circular o arco se debe obtener la derivada respecto al tiempo de dicho arco "<b>s</b>", el cual está dado por:</div><p>
<center>https://images.hive.blog/DQmSB5bg5ZU5e3ege7EPSGMBK2ComfRtTtQv8CYrkf2AYUH/image.png</center>

<div class="text-justify">Diferenciando respecto al tiempo la expresión (3) tenemos:</div><p>
<center>https://images.hive.blog/DQmW7TemsUefCGAiM9KBunvGt2FCbTPRecodW4Wb13gn5zr/image.png</center>

Sustituyendo (3) en (4) se tiene:
<center>https://images.hive.blog/DQmVibSREMdHELMrTM4TgXozht7SjJLsZrZJcSvGGh1ZRC6/image.png</center>

Dado que la longitud del hilo es constante se tiene que:
<center>https://images.hive.blog/DQmdYBapSvfzT4GTiQhRRz9Hm9s93CvHjg9ptVVdrLZ8ymt/image.png</center>

<div class="text-justify">Sustituyendo (6) en (2), la aceleración tangencial queda expresada de la forma:</div>
<center>https://images.hive.blog/DQmXJWJs4QzCkNdYeJW4VeJmrVGxJnCqy381bTibHbdesp6/image.png</center>

<div class="text-justify">Reemplazando la ecuación (7) en (1) y simplificando obtenemos:  </div><p>
<center>https://images.hive.blog/DQmeaQYpoE8cXUnCz79sUSFZtLv5L6MAXm62ddTPzyvSqs9/image.png</center>

Para pequeñas oscilaciones (<b>senθ ≈  θ</b>)
<center>https://images.hive.blog/DQmYxYW2vu6iWWWmhEyeb4hpov2XNHuXp6yfR3Yjo6p9Z7Z/image.png</center>

<div class="text-justify">La ecuación diferencial dada por la expresión (9) se puede escribir de la forma:</div>
<center>https://images.hive.blog/DQmdEmQDhiafwPDepXUwc3kxio2W7p6qnJCLXawYnmLfWPD/image.png</center>

La solución de la ecuación diferencial (10) está dada por: 
<center>https://images.hive.blog/DQmc6paZDDrtkYdDR7vRFEj1uNMEfJCCzxx5KVRFdhPG645/image.png</center>

<div class="text-justify">Donde el término “<b>ω</b>" representa la frecuencia angular y esta dada por:</div>
<center>https://images.hive.blog/DQmQioDUq1pxdEunTs7SWp5cGKGjZ5nLLjZ7nY6EEBScGWK/image.png</center>

Dado que el periodo de oscilación está definido por:

<center>https://images.hive.blog/DQmYhMfD7cN2CM5455PFZkLnedNABSXAtGJQiYd45DPvTG3/image.png</center>

<div class="text-justify">Para el péndulo simple, el periodo queda expresado como: </div>

<center>https://images.hive.blog/DQmTEa5BV4H7jpZ2XYfmXm8MjXpnNLsMy3Sxuni4hqJZxZc/image.png</center>

<div class="text-justify">De esta expresión se observa que para un péndulo en movimiento armónico simple el periodo de oscilación depende de su longitud y de la gravedad.</div><p>

<div class="text-justify">Es esta dependencia la que permite obtener el valor de la gravedad local a partir de diferentes medidas de los valores del periodo de oscilación para determinadas longitudes.</div><p>
<div class="text-justify">A continuación, se muestra la metodología empleada para determinar el valor de la gravedad local a partir de los valores de oscilación del péndulo versus la longitud. </div><p>
<div class="text-justify">Si bien estas lecturas pueden obtenerse con la elaboración de un péndulo simple a partir de materiales básicos, en esta oportunidad utilizaremos el simulador phET para obtener dichas lecturas. </div><p>
<div class="text-justify">En el siguiente video se muestra la obtención de los valores del periodo de oscilación para distintos valores de longitud a través del simulador phET.</div>

https://youtu.be/6M85sRqqTUU

<div class="text-justify">A partir de los valores del periodo de oscilación versus la longitud (ver tabla) obtenidos en la simulación, determinaremos la relación lineal entre el cuadrado de dichos periodos y la longitud, tal y como se muestra en la siguiente grafica. </div>

<center>https://images.hive.blog/DQmNgte87BWUUHPvZHeF2Dyus9AFbu1imGVeMLBr6ZyX7E6/image.png</center>
<center><em><sup>Tabla de valores del periodo de oscilación versus la longitud obtenida del simulador phET</sup></em></center>

<center>https://images.hive.blog/DQmPmiVHv8978h3b6L9Zny4g5GK1VYHe3yaDoYbxz3Hzqem/image.png</center>
<center><em><sup>Obtención de la ecuación lineal del periodo en función de la longitud</sup></em></center>

<div class="text-justify">De la ecuación (14) obtenida en nuestro análisis teórico podemos observar que la relación entre el cuadrado del periodo y la longitud es una recta y esta dada por la expresión:</div>

<center>https://images.hive.blog/DQmTUA8BHDZ2iJPuXBGM8h7xQVm3rDn7bQcD5rfeDdTdes5/image.png</center>

<div class="text-justify">Igualando la ecuación (15) con la expresión de la línea de tendencia obtenida a partir de los valores arrojados por el simulador phET tenemos:</div>

<center>https://images.hive.blog/DQmZrn6XLwzVKz1eEv9NosQqaDZcZafymChkSfxpGeZad4o/image.png</center>

<div class="text-justify">El resultado obtenido nos muestra que la metodología empleada permite obtener el valor de la gravedad, a partir de las variaciones del periodo de oscilación de un péndulo simple debido a las variaciones en su longitud, convirtiendo de esta forma al péndulo simple en un instrumento de medición de un parámetro de importancia en distintas áreas de la ciencia.</div><p>

<div class="text-justify">Gracias por leer mi publicación, espero que el análisis realizado en este trabajo permita fortalecer y consolidar sus conocimientos en el estudio del movimiento oscilatorio de un péndulo simple y su aplicación en la obtención del valor de la gravedad.</div><p>
<div class="text-justify">Si tienes alguna duda, pregunta o sugerencia deja tus comentarios y con mucho gusto te responderé.</div><p>

<h3>Referencias</h3>

* Física para Ciencias e Ingeniería. Fishbane, Gasiorowicz, Thornton. Volumen I. Prentice Hall.
* Física para la Ciencia y la Tecnología. Tipler Mosca. Volumen 1: Mecánica. Oscilaciones y ondas. Termodinámica. 5a edición. Editorial Reverté.
* Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5a edición. Tomo I. McGraw-Hill.
* Física Universitaria. Sears Zemansky, Young Freedman. 9na edición. Volumen 1. Addison Wesley Longman.