Research diaries #8: Weakening differentiability
hive-196387·@mathowl·
0.000 HBDResearch diaries #8: Weakening differentiability
*In high school we all learned about how to compute the derivative. Here we will look at what it means for a function to be differentiable and how to weaken it.* A derivative of a function at a point gives the slope of the tangent at that point. See the pretty figure below. <center> 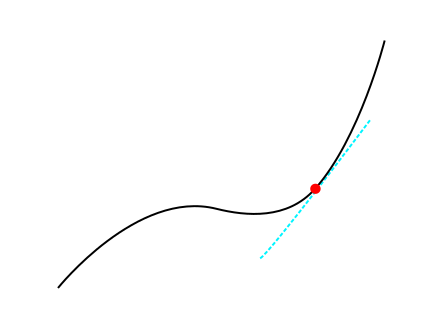 *The blue line we can express as ax+b where a,b are two constants determined by making the line tangent to the black curve. The derivative is given by a* </center> To make it more applied you can think of this graph as a function of position and time. The derivative at a give time then correspond to the speed at that time. Is a derivative always well-defined? No, Let's give an example: <center> 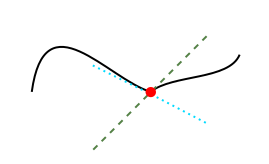 *The black curve is dented. It has a sharp point at the red spot. If we do the previous procedure to find the derivative the derivative could have 2 different values* </center> We see that at the point we want to compute the derivative we could draw 2 different lines that are tangent in two different ways: one approaches from the left and the other approaches from the right. So the derivative is not well defined because the slope can have 2 different values. We call this function not *smooth*. However, these 2 lines still give us information about how steep the function is. This weaker type differentiability is called [Lipschitz continuity](https://en.wikipedia.org/wiki/Lipschitz_continuity). I will skip the mathematical formalities and you can keep your intuitive understanding. So what do functions look like that are not Lipschitz continuous. A simple example is <center>  *A discontinuous curve* </center> The disconintuity makes it so that I cannot draw this double cone shape as before. In the domain of mathematical analysis there is a large field which considers weak versions of properties we considered in a basic calculus course. By weakening these properties we can somehow obtain better results because the conditions are not that severe. Specifically, in the field of differential equations this is a common approach to find solutions of complicated equations which only exist in some weak sense. Maybe that is a nice topic for a future post. <center> *All images made by me ^^* </center> <center> **Cat tax**  </center>
👍 he-index, blainjones, elianaicgomes, cbridges573, urtrailer, jlsplatts, foodfightfriday, kuku-splatts, splatts, w-splatts, gone-hive, weirdheadaches, pixelfan, stempede, chops.support, catinthewindow, regularowl, dandays, kingabesh1, mechanicalowl, inpursuit, sbi4, sbi-tokens, sneakyninja, mastergerund, thedailysneak, babysavage, ravensavage, cryptoknight12, betterdev, rishi556, giftgiver, hextech, mafia.wallet, nftmart, h-e, thecouncil, rishi556.engine, alphacore, cadawg, foxon, pursuant, jd4e, marblely, incinboost, yoyo-jp, marblesz, idig, brofund, brofi, roleerob, nfttunz, caturday.curator, saboin, aulia1993, bluerobo, bilpcoinbpc, blue-witness, irivers, bucipuci, apineda, insaneworks, zuerich, enforcer48, steemseph, adamada, jazzhero, sgbonus, anonymous02, admiralbot, aninsidejob, memehub, steemflagrewards, nathanpieters, chicoduro, yggdrasil.laguna, stemgeeks, stemcuration, adamada.stem, stemline, ruari, star.stem, saboin.stem, babytarazkp, gentleshaid, stemng, samest, kingabesh, the.chiomz, joelagbo, djoi, temitayo-pelumi, teemike, nazom, truth2.stem, lemouth, steemstem-trig, steemstem, dna-replication, roelandp, minnowbooster, aboutcoolscience, robotics101, stemsocial, mobbs, alexander.alexis, analealsuarez, enzor, fragmentarion, flugschwein, purelyscience, nazer, hjmarseille, hyun-soo, ricardoeloy, inibless, sunshine, curie, walterjay, valth, tsoldovieri, wilians, alexdory, de-stem, marcuz, javier.dejuan, cowpatty, zeruxanime, afarina46, laruche, sam9999, temileke, edb, dhimmel, joeyarnoldvn, khalil319, noloafing, aidefr, lottje, sankysanket18, kenadis, anikekirsten, branbello, intrepidphotos, oscurity, pboulet, meanroosterfarm, stem.witness, walterprofe, jsalvage, krrizjos18, vagabond42069, cindynancy, med-hive, superuser3, justtryme90, akipponn, lamouthe, roguewriter, abigail-dantes, zonguin, bhoa, real2josh, dexterdev, geopolis, melvin7, francostem, michaelwrites, deholt, motherofalegend, crowdwitness, apokruphos, aicu, mrhaldar, delilhavores, kyleana, noelyss, maar, germangenius, onewolfe, ehizgabriel, dyptre, prosocialise, vankushfamily, techslut, oluwatobiloba, samminator, neumannsalva, cahlen, witkowskipawel, newtrailers, hivebuzz, chubb149, lugaxker, lpv, zerotoone, torico, therealwolf, toocurious, zmx, koenau, jtm.support, steemean, bubblegif, aries90, archangel21, scottcbusiness, cakemonster, treefiddybruh, hive-world, traderhive, axelx12, roomservice, smartsteem, hiveonboard, ausbit.dev, iansart, princessmewmew, bil.prag, c0wtschpotato, yaelg, cloh76, stayoutoftherz, soufiani, epicdice, riazud, alt3r, doodleaday, ambicrypto, mvd, hhayweaver, gunthertopp, meno, hetty-rowan, vonaurolacu, honeycup-waters, peterpanpan, rencongland, aboutyourbiz, zipsardinia, javyeslava.photo, steemdiamond, vragolana, stickchumpion, frissonsteemit, petertag, aicoding, tomatom, filosof103, marcolino76, indigoocean, josesalazar200, tristancarax, battebilly, utube, neneandy, positiveninja, palasatenea, chucknun, dcrops, eftnow, phgnomo, multifacetas, peterale, sunsea, stahlberg, rambutan.art, diosmarymaiz1, solox, aabcent, thecryptodrive, apsu, detlev, revo, cryptocoinkb, edithbdraw, cosplay.hadr, boynashruddin, fatman, lucksacks.com, devann, eturnerx-honey, dumitriu, minerthreat, zirky, schmidi, rawecz, seinkalar, aichanbot, driptorchpress, rt395, trevorpetrie, jigstrike, pandasquad, kristall97, miroslaviv, benwickenton, genepoolrentsclr, joshglen, gordon92, reizak, zipporah, clpacksperiment, alaqrab, dashfit, minnowpowerup, leomarylm, kgakakillerg, cheese4ead, gohive, meritocracy, drhueso, mistural, martibis, florian-glechner, baycan, cryptocopy, knightsunited, wrestorgonline, justfavour, serylt, sawyn, iumac03, goodcontentbot, kgswallet, dejan.vuckovic, fineartnow, jfuji, cryptononymous, nateaguila, perpetuum-lynx, mind.force, blockgolem, cnfund, appleskie, dipom98, greddyforce, diabonua, bflanagin, sandymeyer, lizanomadsoul, pepskaram, myach, outtheshellvlog, steemstorage, anthony2019, merit.ahama, stephen.king989, videosteemit, jjerryhan, therising, steemcryptosicko, freddio.sport, limn, okluvmee, howiemac, mulletwang, thelordsharvest, gabrielatravels, steemvault, theawesononso, coindevil, sorin.cristescu, foxyspirit, altleft, labeba1969, sc000, diabolika, steveconnor, yoghurt, photohunt, brianoflondon, qberry, podping, arunava, hdmed, themonkeyzuelans, takowi, flyerchen, hurtlocker, punchline, didic, bluemaskman, tggr, hadrgames, cugel, upme, endrius, rent-an-ape, privex, chasmic-cosm, derosnec, felt.buzz, steemwizards, nerdnews, rocky1, vera-vaders-ea, karaoke1850, notb4mycoffee, silverwhale, ilovecryptopl, autobodhi, jessicaossom, tazbaz, quinnertronics, drricksanchez, xrocky1, modernzorker, bitrocker2020, ew-and-patterns, lenasveganliving, vittoriozuccala, thelittlebank, the.success.club, hairgistix, netaterra, justyy, newsflash, irgendwo, antisocialist, raynen, proxy-pal, rosana6, kevinwong, juanmiguelsalas, evagavilan2, freebornsociety, steemed-proxy, roamingsparrow, jmsansan.leo, failingforwards, drexlord, the-grandmaster, tfeldman, iamsaray, federacion45, zyx066, steem4all, armandosodano, artsyproxy, trippymane, the-burn, blewitt, ambyr00, guchtere, redrica, bartosz546, onestop, michelle.gent, nathyortiz, brotherhood, miroslavrc, francosteemvotes, rmach, mcsvi, zest, meanbees, elevator09, forykw, erick1, mproxima, sanderjansenart, vixmemon, elements5, ykretz, hivecoffee, davideazul, mirteg, njclabaugh, duke77, atheistrepublic, dondido, jerrybanfield, lordvader, randumb, proto26, bigtakosensei, yehey, uche-nna, abachon, sevenoh-fiveoh, sagarkothari88, peaceandwar, yjcps, fatkat, robmojo, drifter1, mammasitta, binkyprod, prapanth, cordeta, aotearoa, mariusfebruary, roozeec, lxsxl, danaedwards, shinedojo, vegan.niinja, beerlover, ragnarhewins90, drsensor, marcoriccardi, kieranstone, gribouille, eric-boucher, stevenwood, robertbira, nicole-st, imcore, flatman, chrisdavidphoto, jim888, hope-on-fire, peerfinance, bluefinstudios, krishu.stem, busybody, ace108, joseluis91, cryptomaso, careassaktart, xmauron3, gamersclassified, holovision.stem, gaottantacinque, cribbio, gasaeightyfive, apunawu, agmoore, moraviareosa, aliriera, borjan, profwhitetower,