https://youtu.be/pfpd8RJi9jw

In this video I explore why the shape of cans that you see in the supermarket are the way they are and use calculus to determine what ratios of can height to can radius are used in real life. This is an applied project question in my calculus text book and I thought it was really interesting and worth doing a math easy on it! Enjoy!

---

Watch video on:

- 3Speak: []()
- Odysee: [https://odysee.com/@mes:8/applied-project-the-shape-of-a-can-the:0](https://odysee.com/@mes:8/applied-project-the-shape-of-a-can-the:0)
- BitChute: [https://www.bitchute.com/video/YeIOWEQoARCo/](https://www.bitchute.com/video/YeIOWEQoARCo/)
- Rumble: []()
- DTube: []()
- YouTube: [https://youtu.be/pfpd8RJi9jw](https://youtu.be/pfpd8RJi9jw)

Download video notes: https://1drv.ms/b/s!As32ynv0LoaIiaVwg0FLYrhmuJLiUA?e=acxCHW

---

# View Video Notes Below!

---

>Download these notes: Link is in video description.
>View these notes as an article: https://peakd.com/@mes
>Subscribe via email: http://mes.fm/subscribe
>Donate! :) https://mes.fm/donate
>Buy MES merchandise! https://mes.fm/store 
>More links: https://linktr.ee/matheasy
>**Follow my research in real-time on my MES Links Telegram:** https://t.me/meslinks
>Subscribe to MES Truth: https://mes.fm/truth
>
>Reuse of my videos:
>- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
>
>Fight back against censorship:
>- Bookmark sites/channels/accounts and check periodically
>- Remember to always archive website pages in case they get deleted/changed.
>
>Recommended Books:
>- "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
>
>Join my forums!
>- Hive community: https://peakd.com/c/hive-128780
>- Reddit: https://reddit.com/r/AMAZINGMathStuff
>- Discord: https://mes.fm/chatroom
>
>Follow along my epic video series:
>- #MESScience: https://mes.fm/science-playlist
>- #MESExperiments: https://peakd.com/mesexperiments/@mes/list
>- #AntiGravity: https://peakd.com/antigravity/@mes/series
>-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!
>- #FreeEnergy: https://mes.fm/freeenergy-playlist
>- #PG (YouTube-deleted series): https://peakd.com/pg/@mes/videos
>
>---
>
>NOTE #1: If you don't have time to watch this whole video:
>
>- Skip to the end for Summary and Conclusions (if available)
>- Play this video at a faster speed.
>-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
>-- MES tutorial: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website
>- Download and read video notes.
>- Read notes on the Hive blockchain #Hive
>- Watch the video in parts.
>-- Timestamps of all parts are in the description.
>
>Browser extension recommendations: 
>
>- Increase video speed: https://mes.fm/videospeed-extension
>- Increase video audio: https://mes.fm/volume-extension
>- Text to speech: https://mes.fm/speech-extension
>--Android app: https://mes.fm/speech-android

---

# The Science behind the size and shape of a can

![Applied Project 2 - Shape of a Can.jpg](https://files.peakd.com/file/peakd-hive/mes/23yxA2F9qJBSvNtN2YHB4bETNGQdAwZRCiGeUPeSKieDqmNMeuz8mbRMWsUwFkPhZNzuc.jpg)

# Applied Project: The Shape of a Can

The Applied Project can be found here: [LINK](https://1drv.ms/b/s!As32ynv0LoaIiaVv272QUmL_lZHf6w?e=XkDQqb)

In this project we investigate the most economical shape for a can.

We first interpret this to mean that the volume **V** of a cylindrical can is given and we need to find the height **h** and radius **r** that minimize the cost of the metal to make the can (see the figure below).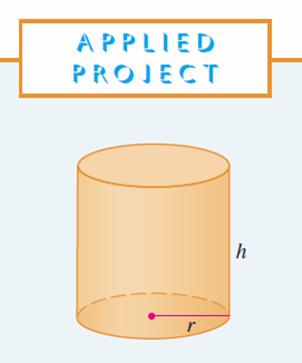

![image.png](https://files.peakd.com/file/peakd-hive/mes/23z7dVgDvPPVUt4KQTD9rWvu8b95TqTqnNHzvK7dMwfUbDKeNksjFmwjoDFz6JogY3iqb.png)

If we disregard any waste metal in the manufacturing process, then the problem is to minimize the surface area of the cylinder.

We solved this problem in my earlier [Example 2 video](http://youtu.be/qU5WQOo9JA8), and we found that **h = 2r**; that is, the height should be the same as the diameter.

But if you go to your cupboard or your supermarket with a ruler, you will discover that the height is usually greater than the diameter and the ratio **h/r** varies from **2** up to about **3.8**.

Let's see if we can explain this phenomenon.

---

# Question 1

The material for the cans is cut from sheets of metal.

The cylindrical sides are formed by bending rectangles; these rectangles are cut from the sheet with little or no waste.

But if the top and bottom discs are cut from squares of side 2r (as in the figure below), this leaves considerable waste metal, which may be recycled but has little or no value to the can makers.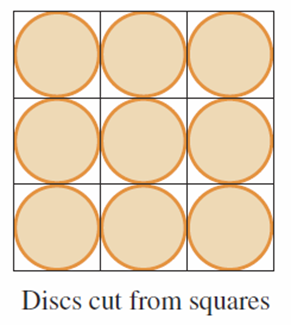

![image.png](https://files.peakd.com/file/peakd-hive/mes/23xLL41dMis6q1bfGJcq49iLVHKF7Q2QAFn1xSWwePdYeQ7zDkPrbZqWrcMrEZAm48ppR.png)

If this is the case, show that the amount of metal used is minimized when: 

![image.png](https://files.peakd.com/file/peakd-hive/mes/48Hh6AiUppFFu4niVKtxHjG7BszJPHir69hTVqSHfGGnxSsUR2jcMw5QPWYJJmwkMK.png)

## Solution to Question 1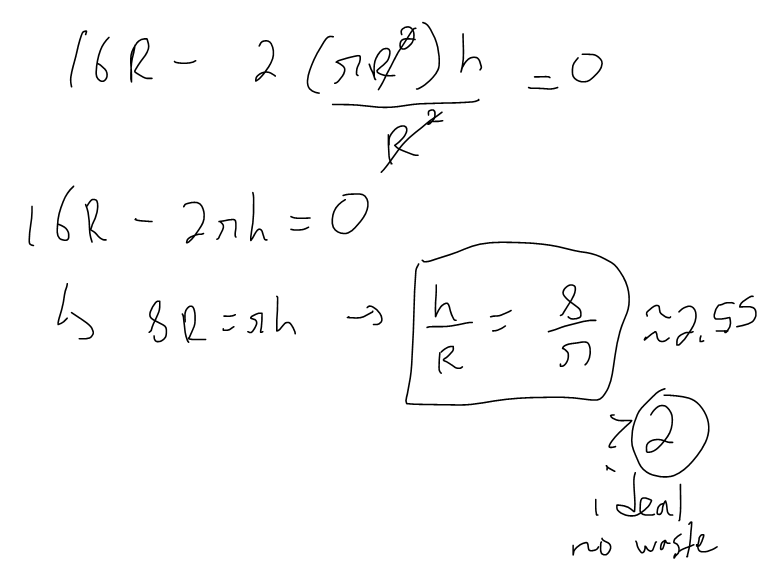

![image.png](https://files.peakd.com/file/peakd-hive/mes/23tHbKgeDDyNjvw2NG8u8Qe1ysDYFDC3VdgxV7z9kcUogdrg5WiYxYuNJZUHCMLU8eL8T.png)

![image.png](https://files.peakd.com/file/peakd-hive/mes/23t8EjqhGLKGibkhMyhNDEoqB61WudS4ENWU4aQycqZALqiyFFynJixzDKinjvdCn98yN.png)

---

# Question 2

A more efficient packing of the discs is obtained by dividing the metal sheet into hexagons and cutting the circular lids and bases from the hexagons (see the figure below).

![image.png](https://files.peakd.com/file/peakd-hive/mes/EpJdw1BrTGQSxXLtK7fDArnMuCAUgaXRESBcYL1bZ4unu9z7wo1etPtXK88hBGLSugQ.png)

Show that if this strategy is adopted, then:

![image.png](https://files.peakd.com/file/peakd-hive/mes/23tw5ZHqZ9rRhH9jwXR5Gqr2DzmSTQRgLEYfC9rruBRybr21repegX1uuWERKDQweaHEB.png)

## Solution to Question 2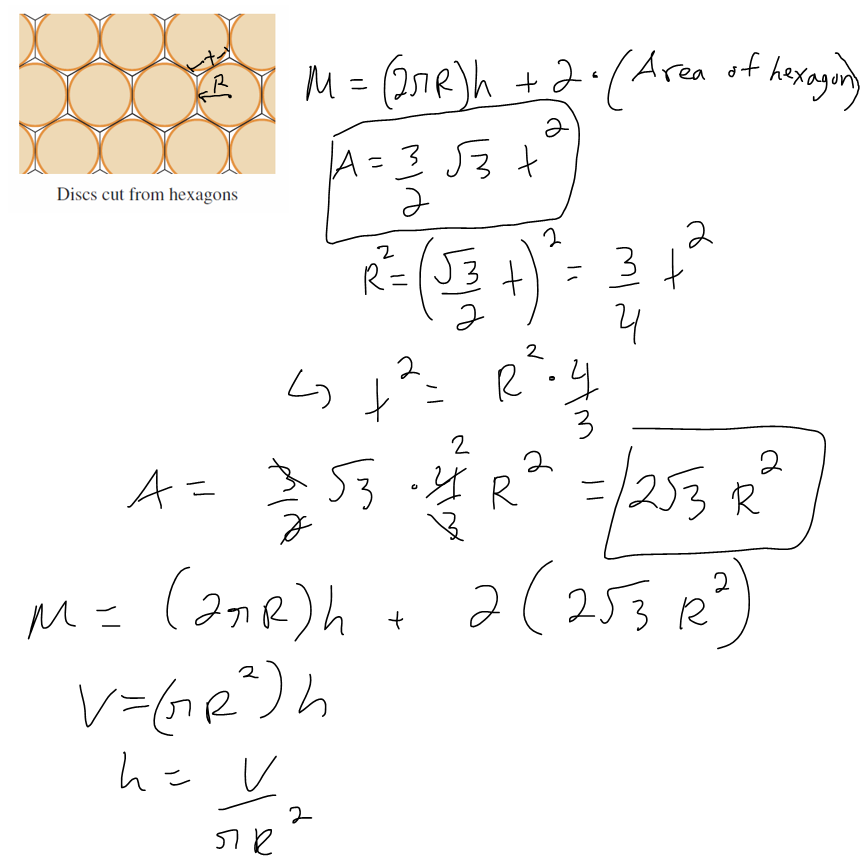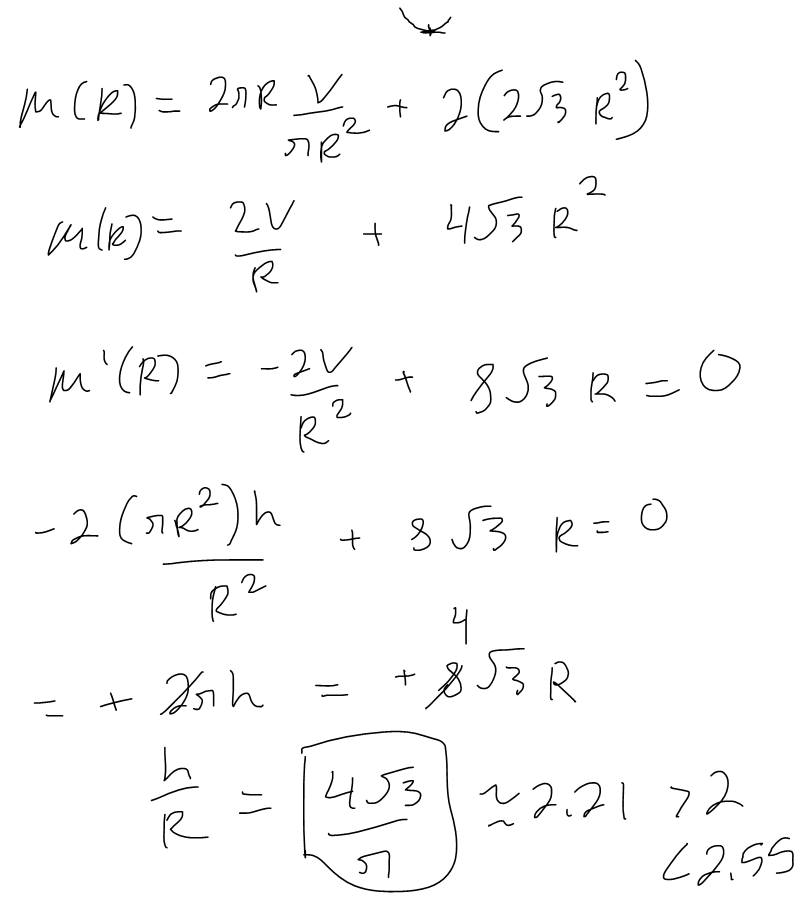

![image.png](https://files.peakd.com/file/peakd-hive/mes/23sxozwVBhaqSXu4ksvwyefGgkLwNCbqoTSDRzri5mXLHN1y2spDPzju2VCpf4KQkoUBN.png)

![image.png](https://files.peakd.com/file/peakd-hive/mes/23t8EjqhG7aN2DL2fyUDYbu4q6LUCDAokHd7Pq52WcRgEJZKmremg2f4GvGqhQsehsLwD.png)

___

# Question 3

The values of **h/r** that we found in Questions 1 and 2 are a little closer to the ones that actually occur on supermarket shelves, but they still don't account for everything.

If we look more closely at some real cans, we see that the lid and the base are formed from discs with radius larger than **r** that are bent over the ends of the can.

If we allow for this we would increase **h/r**.

More significantly, in addition to the cost of the metal we need to incorporate the manufacturing of the can into the cost.

Let's assume that most of the expense is incurred in joining the sides to the rims of the cans.

If we cut the discs from the hexagons as in Question 2, then the total cost is proportional to: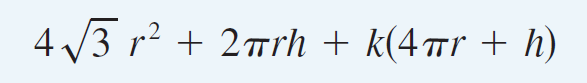

![image.png](https://files.peakd.com/file/peakd-hive/mes/Eoib5ocuC4W53v7gbXo7whHEtJGHaSjcnYoMTjci13o6VE1uawM4xE7C2wae4C7qVAy.png)

where **k** is the reciprocal of the length that can be joined for the cost of one unit area of metal.

Show that this expression is minimized when:

![image.png](https://files.peakd.com/file/peakd-hive/mes/EoH4GUxcQ9NCrLLCMG7kDRvRZuzbwk5UHHG6Y6K1oz62TqELthWuvUvEo69RBidU1xk.png)

## Solution to Question 3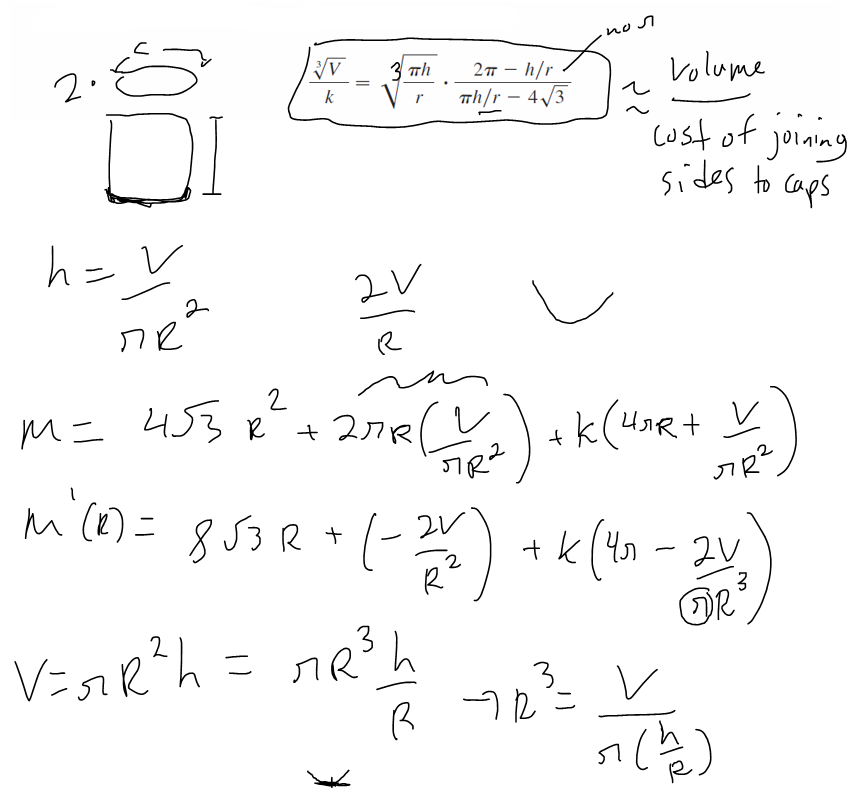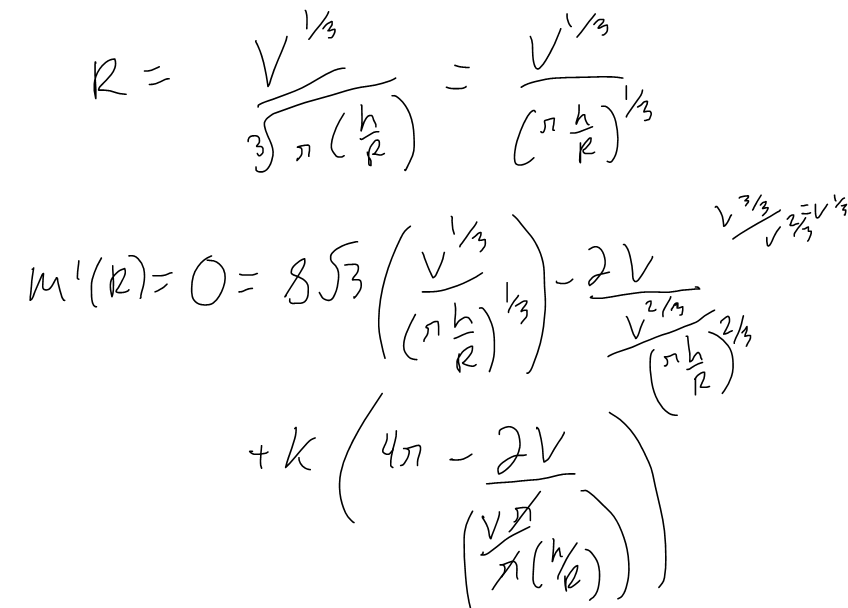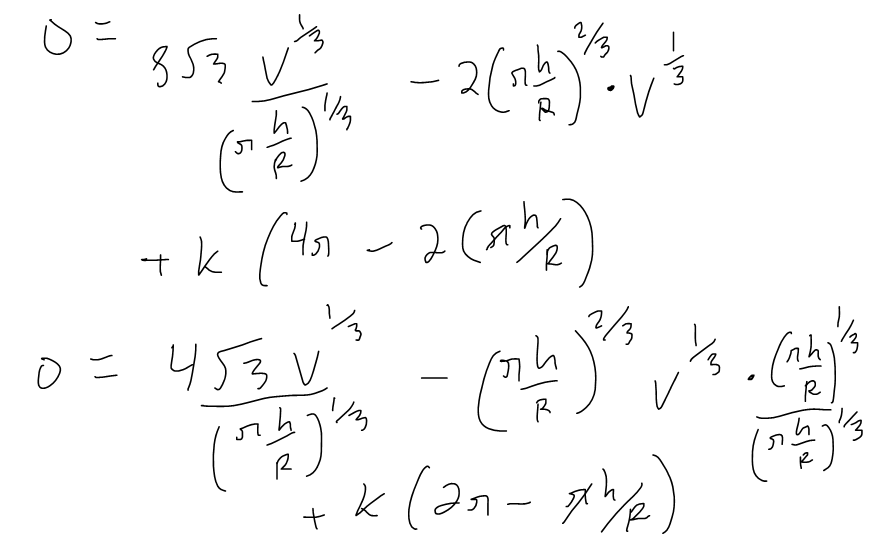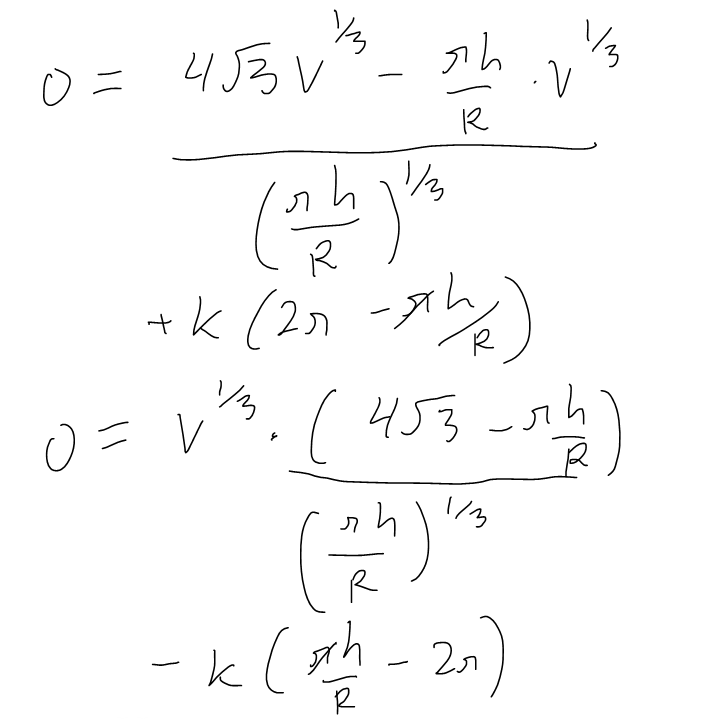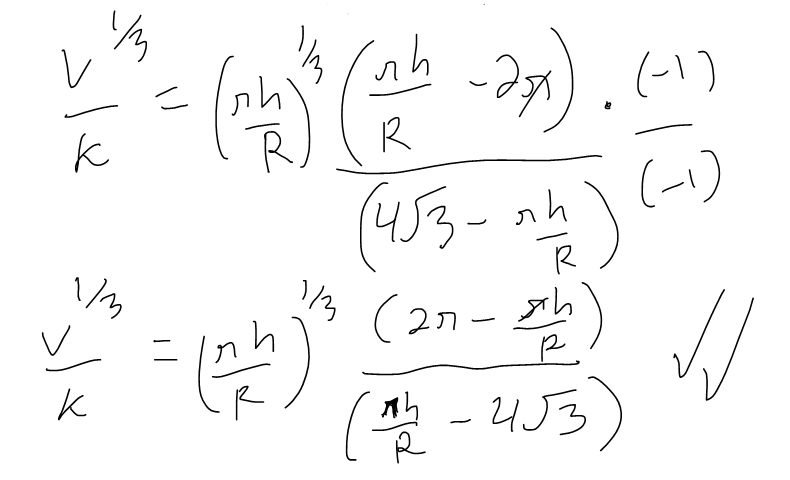

![image.png](https://files.peakd.com/file/peakd-hive/mes/Enz3wpJzbP7CKsLUpSHvM1vZ1J3mSoRRdwAdnXBXhB8TLe4zde1mNnTsDnUnnfpP7p9.png)

![image.png](https://files.peakd.com/file/peakd-hive/mes/23tHbr9ykyPT31L9dhh4J2EVJDf3bFG5gCyyYFXeWCbPFP15DH8qhNqzRqkD25PdXhqi7.png)

![image.png](https://files.peakd.com/file/peakd-hive/mes/23t8DBnQF2rBvRWuZJT9FxHLX7699v3uCo3SCpZiq5E31V4WGGtzgZyBGh4WPPNJ3Cz7a.png)

![image.png](https://files.peakd.com/file/peakd-hive/mes/23tT24arHMipW7Y5hkkzf61ZNzYuhGs2vRiDx41ygPWFJqdtRcCtozpn2qvAGQ42nNxVf.png)

![image.png](https://files.peakd.com/file/peakd-hive/mes/23tHbKgySGjdy1cWXmw32muRmTNmskieQHAS2gXBng2xx9MkCAzW3w3t5h4spfgd9CQ41.png)

---

# Question 4

Plot **V<sup>1/3</sup>/k** as a function of **x = h/r** and use your graph to argue that when a can is large or joining is cheap, we should make **h/r** approximately 2.21 (as in Question 2).

But when the can is small or joining is costly, **h/r** should be substantially larger.

## Solution to Question 4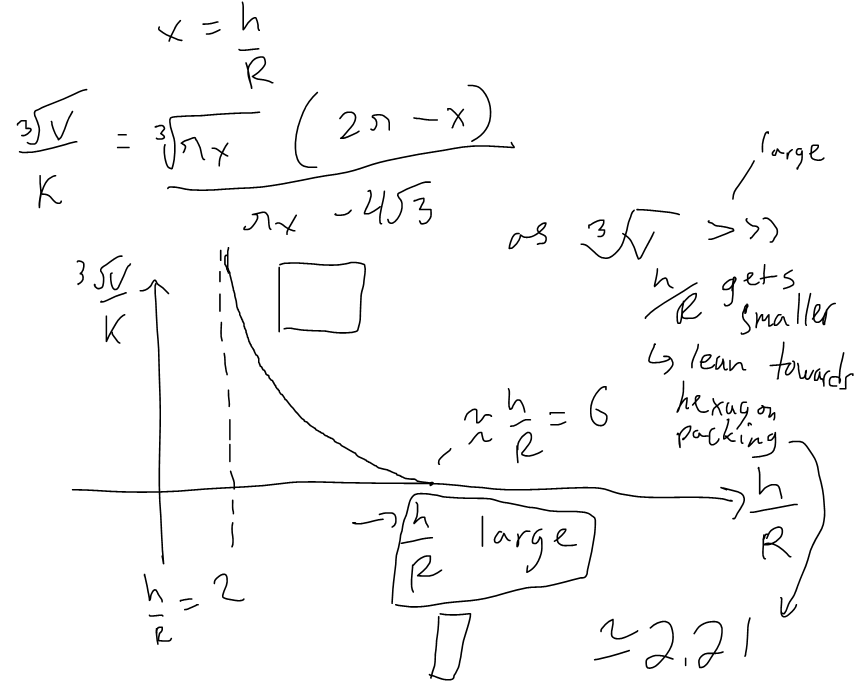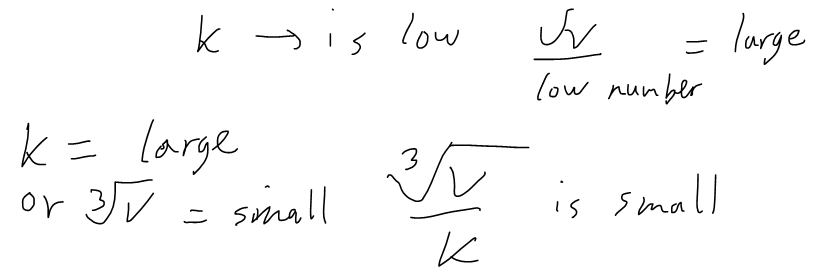

![image.png](https://files.peakd.com/file/peakd-hive/mes/23t8DBnQFDCA1kxYmrUvwywYtajpV2Vu6UooVyf4ykUoTYSsBS2XXYGqLqePk1kHsZo9G.png)

![image.png](https://files.peakd.com/file/peakd-hive/mes/Eo2BTut2nd6jF5AZGWkXdVEKoPWTh9Hx7bGrGR2oXbdZcVNrJGR4ugUhXxEVbdgvXKq.png)

---

# Question 5

Our analysis shows that large cans should be almost square but small cans should be tall and thin.

Take a look at the relative shapes of the cans in a supermarket.

Is our conclusion usually true in practice?

Are there exceptions?

Can you suggest reasons why small cans are not always tall and thin?

## Solution to Question 5

Yes, in practice most small cans are tall and thin while most large cans are almost square. 

But yes, there are exceptions to this conclusions.

Some reasons for the exceptions are listed below:

- Different materials = different costs of manufacturing / materials and have different properties.
- Different manufacturing process.
- Some materials, such as plastic, can be formed directly with a mold.
- Better technology may be available.
- Specific consumer needs and wants.