<liketuimages>
<center>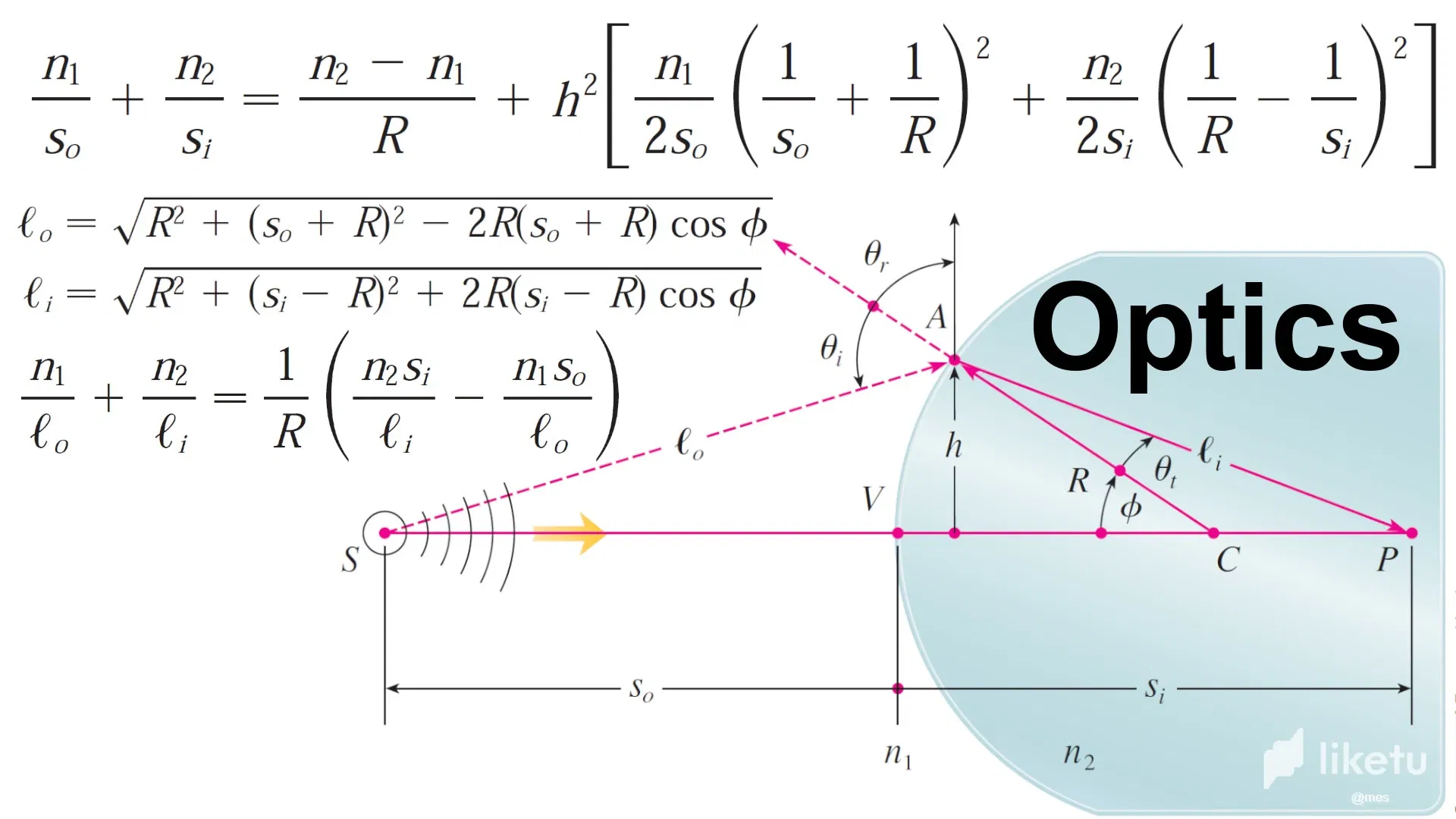
![2QbPkWQaSfr8L43p_8_Exercise_2_Optics.webp](https://cdn.liketu.com/media/mes/images/2QbPkWQaSfr8L43p_8_Exercise_2_Optics/2QbPkWQaSfr8L43p_8_Exercise_2_Optics.webp)
</center>
</liketuimages>

In this video, I derive the first-order and third-order optics formulas by approximating the refraction formula for light using first and third-order Taylor polynomials, respectively. [https://youtu.be/leZ0QK_n07k](https://youtu.be/leZ0QK_n07k)

---

For the best experience view this post on [Liketu](https://liketu.com/@mes/exercise-2-deriving-the-1st-order-and-3rd-order-optics-formulas)

👍 stemcur, quinnertronics, jerrybanfield, irivers, mes, mama21, antisocialist, freebornsociety, yayogerardo, hive-129556, trayan, artgrafiken, peerfinance, fw206, steemmonsterking, tracer-paulo, holovision.stem, teacherspet, curie, steemiteducation, privex, azizbd, roseri, litzney, kylealex, samsemilia7, cindycam, schoolforsdg4, affiedalfayed, rocky1, aidefr, masterwu, misterbob, ejlo3310, ruth-elise, jjerryhan, foxyspirit, broncofan99, aceaeterna, witkowskipawel, davidbright, azj26, gamemapmaker, rhemagames, amberyooper, bigdizzle91, skycae, achimmertens, ikill4yo0, the-burn, pepskaram, tggr, seinkalar, baboz, finkistinger, bflanagin, cnfund, mobbs, sustainablyyours, minnowbooster, torico, pandasquad, zipporah, certain, priyandaily, evagavilan2, jesus-son, the.success.club, mhel, r00sj3, the100, zmx, minerthreat, melor9, reverseacid, magnacarta, joshglen, diabolika, aicu, baltai, anafae, gordon92, ilovecryptopl, therealwolf, merlin7, kaylinart, jacor, modernzorker, edu-venezuela, education-hive, c0wtschpotato, boynashruddin, jigstrike, armandosodano, palasatenea, newtrailers, humbe, edithbdraw, smartsteem, tobias-g, hiveonboard, ausbit.dev, tfeldman, pipiczech, steemcryptosicko, iamsaray, jessicaossom, vickoly, cloh76, putu300, double-negative, dawnoner, stickchumpion, didic, brianoflondon, multifacetas, dcrops, rencongland, epicdice, tinyhousecryptos, coindevil, revo, tiffin, nozzy, henrietta27, b8l, indigoocean, kristall97, treasuree, ambyr00, dejan.vuckovic, greddyforce, apshamilton, hamismsf, javyeslava.photo, jpbliberty, podping, juanmiguelsalas, boxcarblue, dhimmel, irisworld, annabeth, balabambuz, felt.buzz, minnowpowerup, chris-uk, monica-ene, tawadak24, drricksanchez, okluvmee, drhueso, baycan, me2selah, cryptononymous, cliffagreen, steemean, noctury, eliel, bitrocker2020, samminator, yoghurt, allentaylor, kevinwong, rt395, amphlux, movingman, yixn, machan, jijisaurart, kenadis, cryptocoinkb, bluemaskman, tokensink, hadrgames, esmeesmith, steveconnor, carn, steemstorage, joseq1570, visualartist, newilluminati, bscrypto, flyerchen, lukasbachofner, aboutyourbiz, neumannsalva, investingpennies, bennettitalia, fantasycrypto, yaelg, cakemonster, bernardino, frissonsteemit, thelordsharvest, steemvault, communitybank, utube, sportscontest, videosteemit, photohunt, superlotto, melbourneswest, citizendog, cheese4ead, beta500, knightsunited, benwickenton, hhayweaver, atomcollector, vittoriozuccala, talentclub, altleft, whywhy, trippymane, arunava, zyx066, stevenson7, steem.services, aicoding, omarrojas, outtheshellvlog, torkot, oscarina, neneandy, qwerrie, h3m4n7, zerotoone, princessmewmew, dipom98, nateaguila, justfavour, juancar347, decomoescribir, dresden.theone, federacion45, tazbaz, myach, adelepazani, therising, proxy-pal, archangel21, detlev, chasmic-cosm, dune69, marc-allaria, irgendwo, autobodhi, gloriaolar, hive-199963, leomarylm, littlesorceress, noalys, lemouth, stayoutoftherz, steemed-proxy, hairgistix, battebilly, followjohngalt, h-hamilton, hetty-rowan, positiveninja, filmmaking4hive, valth, fineartnow, softa, steemegg, asado, clpacksperiment, abu78, bil.prag, michelle.gent, endersong, sunsea, melvin7, saravm82, failingforwards, nathyortiz, limn, technico, hikergirl, gunthertopp, justyy, gabrielatravels, metroair, empath, phgnomo, qberry, steemdiamond, krisconkr, hubeyma, blingit, belug, whitneyalexx, enjar, stahlberg, cryptofiloz, cryptosneeze, tristancarax, driptorchpress, rondonshneezy, traderhive, sc000, lichtkunstfoto, alaqrab, onemedia, ambicrypto, acantoni, yadamaniart, meno, sco, goblinknackers, kiemurainen, cosplay.hadr, aries90, bartosz546, doctor-cog-diss, yozen, elgatoshawua, atexoras.pub, instamental, yangyanje, ahmedsy, nickelbunker, meritocracy, thelittlebank, ibt-survival, mproxima, sanderjansenart, vixmemon, robibasa, reggaesteem, hivecoffee, holovision.cash, mirteg, vindiesel1980, shawnnft, pladozero, bigtakosensei, bushradio, bartheek, uche-nna, hivelist, sevenoh-fiveoh, hk-curation, wasined, ganjafarmer, hashkings, peaceandwar, meanbees, drifter1, buttcoins, cordeta, aiziqi, mariusfebruary, lettinggotech, danaedwards, shinedojo, vegan.niinja, leilanyarevalo, beerlover, deisip67, marcoriccardi, afifa, mashiliyanage, kieranstone, vaultec, nfttunz, eric-boucher, nicole-st, lk666, oscarcede, chrisdavidphoto, guada1, nwjordan, apteacher, bluefinstudios, m1alsan, joseluis91, gamersclassified, titusfrost,